题目链接

最大半连通子图

题目描述

一个有向图 $G=\left(V,E\right)$ 称为半连通的 (Semi-Connected)，如果满足：$\forall u,v\in V$，满足 $u\to v$ 或 $v\to u$，即对于图中任意两点 $u,v$，存在一条 $u$ 到 $v$ 的有向路径或者从 $v$ 到 $u$ 的有向路径。

若 $G^{\prime }=\left(V^{\prime },E^{\prime }\right)$ 满足 $V^{\prime }\subseteq V$，$E^{\prime }$ 是 $E$ 中所有跟 $V^{\prime }$ 有关的边，则称 $G^{\prime }$ 是 $G$ 的一个导出子图。若 $G^{\prime }$ 是 $G$ 的导出子图，且 $G^{\prime }$ 半连通，则称 $G^{\prime }$ 为 $G$ 的半连通子图。若 $G^{\prime }$ 是 $G$ 所有半连通子图中包含节点数最多的，则称 $G^{\prime }$ 是 $G$ 的最大半连通子图。

给定一个有向图 $G$，请求出 $G$ 的最大半连通子图拥有的节点数 $K$，以及不同的最大半连通子图的数目 $C$。由于 $C$ 可能比较大，仅要求输出 $C$ 对 $X$ 的余数。

输入格式

第一行包含两个整数 $N,M,X$。$N,M$分别表示图 $G$ 的点数与边数，$X$ 的意义如上文所述。

接下来 $M$ 行，每行两个正整数 $a,b$，表示一条有向边 $\left(a,b\right)$。图中的每个点将编号为 $1,2,3\dots N$，保证输入中同一个$\left(a,b\right)$不会出现两次。

输出格式

应包含两行，第一行包含一个整数 $K$，第二行包含整数 $C\mathrm{mod}X$。

样例 #1

样例输入 #1

6 6 20070603
1 2
2 1
1 3
2 4
5 6
6 4

样例输出 #1

3
3

提示

对于 $100\%$ 的数据，$N\le 10^5$，$M\le 10^6$，$X\le 10^8$。

算法思想

根据题目描述，要求出 $G$ 的最大半连通子图拥有的节点数 $K$，以及不同的最大半连通子图的数目 $C$。
测试样例如下图所示，图中最大半连通子图有 { 1 , 2 , 4 } \{1,2,4\} {1,2,4}、 { 2 , 1 , 3 } \{2,1,3\} {2,1,3}、 { 5 , 6 , 4 } \{5,6,4\} {5,6,4}，都拥有$3$个节点。

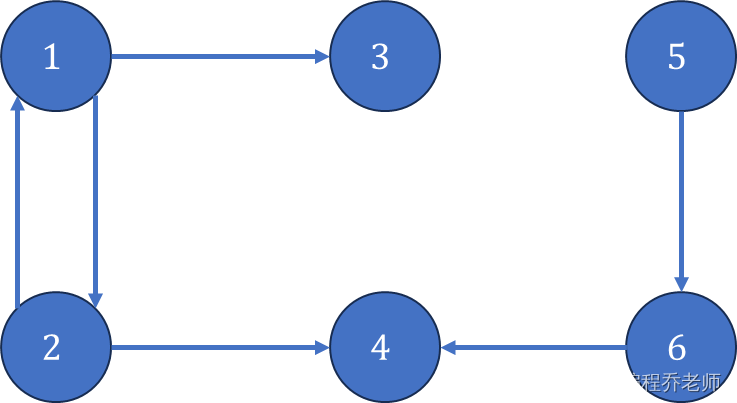
由于图中可能存在环，不方便直接求解。考虑先求强连通分量，然后进行缩点得到DAG（有向无环图），在拓扑序列中使用动态规划的思想求图中的最长链，以及最长链的个数。关于强连通分量，可以参考博主的另一篇文章——每周算法：强连通分量。

算法实现

• 首先用Tarjan算法求强连通分量，然后缩点得到DAG
• 在拓扑序列中使用动态规划的思想：
  • 定义状态$f[u]$表示以$u$为终点的最长链的长度，状态$g[u]$表示以$u$为终点的最长链的个数
  • 若存在一条边$u\to v$的：
    • 如果$f[v]<f[u]+scc\_size[v]$，$f[v]=f[u]+scc\_size[v],g[v]=g[u]$，其中$scc\_size[v]$表示$v$所在强连通分量中点的个数。
    • 否则如果$f[v]=f[u]+scc\_size[v]$，$g[v]=g[v]+g[u]$
• 最终打擂台求最长链的长度，已经该长度的方案数

代码实现

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
//由于缩点后还要添加边，因此边数×2
const int N = 1e5 + 5, M = 2e6 + 5; 
int h[N], hd[N], e[M], ne[M], idx; //hd存储DAG的邻接表
int n, m, mod;
int dfn[N], low[N], timestamp, stk[N], top, scc_cnt, id[N], scc_size[N];
bool in_stk[N];
int f[N], g[N];
void add(int h[], int a, int b)  // 在邻接表h中添加一条边a->b
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[++ top] = u, in_stk[u] = true;
    for(int i = h[u]; ~ i; i = ne[i])
    {
        int v = e[i];
        if(!dfn[v])
        {
            tarjan(v);
            //如果low[v]更小，则使用low[v]更新low[u]，因为u可以到达v，所以v能回溯到时间戳，u也必然能到
            low[u] = min(low[u], low[v]);
        }
        else if(in_stk[v]) //v点已经遍历过了，并且还在栈中，说明v是u的后向边或者横叉边连接的点
        {
             //那么v点的时间戳一定小于u点的时间戳
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(dfn[u] == low[u]) //如果u能回溯到的最早时间戳就是自己，那么u必然是其所在强连通分量最早被访问的点
    {
        scc_cnt ++;
        int v; 
        do
        {
            v = stk[top --]; //弹出栈中该强连通分量中的点
            in_stk[v] = false;
            id[v] = scc_cnt;
            scc_size[scc_cnt]++; //统计该强连通分量中点的数量
        }while(u != v);
    }
    
}
int main()
{
    scanf("%d%d%d", &n, &m, &mod);
    memset(h, -1, sizeof h);
    memset(hd, -1, sizeof hd);
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(h, a, b);
    }
    
    for(int i = 1; i <= n; i ++)
        if(!dfn[i]) tarjan(i); //tarjan求强连通分量
    
    unordered_set<int> S; //保存每条边的哈希值，防止重边  
    //基于强连通分量构建DAG
    for(int u = 1; u <= n; u ++)
        for(int i = h[u]; ~ i; i = ne[i])
        {
            int v = e[i];
            int a = id[u], b = id[v];
            LL hash = a * 1000000ll + b; //分配一个哈希值
            if(a != b && !S.count(hash)) //不在同一个强连通分量中，并且不是重边
            {
                add(hd, a, b);
                S.insert(hash);
            }
        }
    //在拓扑序列中求解最长链的长度和方案数
    for(int u = scc_cnt; u > 0; u --)
    {
        if(!f[u]) //初始状态
        {
            f[u] = scc_size[u];
            g[u] = 1;
        }
        for(int i = hd[u]; ~ i; i = ne[i])
        {
            int v = e[i];
            if(f[v] < f[u] + scc_size[v])
            {
                f[v] = f[u] + scc_size[v];
                g[v] = g[u];
            }
            else if(f[v] == f[u] + scc_size[v])
            {
                g[v] = (g[v] + g[u]) % mod;
            }
        }
    }
    
    int maxn = 0, sum = 0; //求最长链的长度和方案数
    for(int i = 1; i <= scc_cnt; i ++)
    {
        if(f[i] > maxn)
        {
            maxn = f[i];
            sum = g[i];
        }
        else if(f[i] == maxn) sum = (sum + g[i]) % mod;
    }
    printf("%d\n%d\n", maxn, sum);
    return 0;
        
}