首先记得一个知识点

在旋转矩阵中，旋转矩阵的逆矩阵就是旋转矩阵的转置，这个矩阵是正交矩阵

我们需要做到的就是观测变换，这个变换包括视图变换和投影变换（投影变换包含正交变换和透视变换）

三维变换复习

首先复习一下三维变换，三维变换在二维变换的基础上添加一个维度，首先我们在之前的学习中可以了解到，物体的旋转和缩放都可以通过一个矩阵来表示，但是位移比较特殊，如果我们需要完整的描述一个物体在空间内的变换，就需要做到仿射变换+位移变换

为了解决这个问题，我们才引入了齐次坐标，也就是说，将每一个坐标扩展一维，最后一个数为0时代表为一个向量，最后一个坐标为1时代表为一个点，这样做旋转，缩放和位移都可以通过矩阵来表达

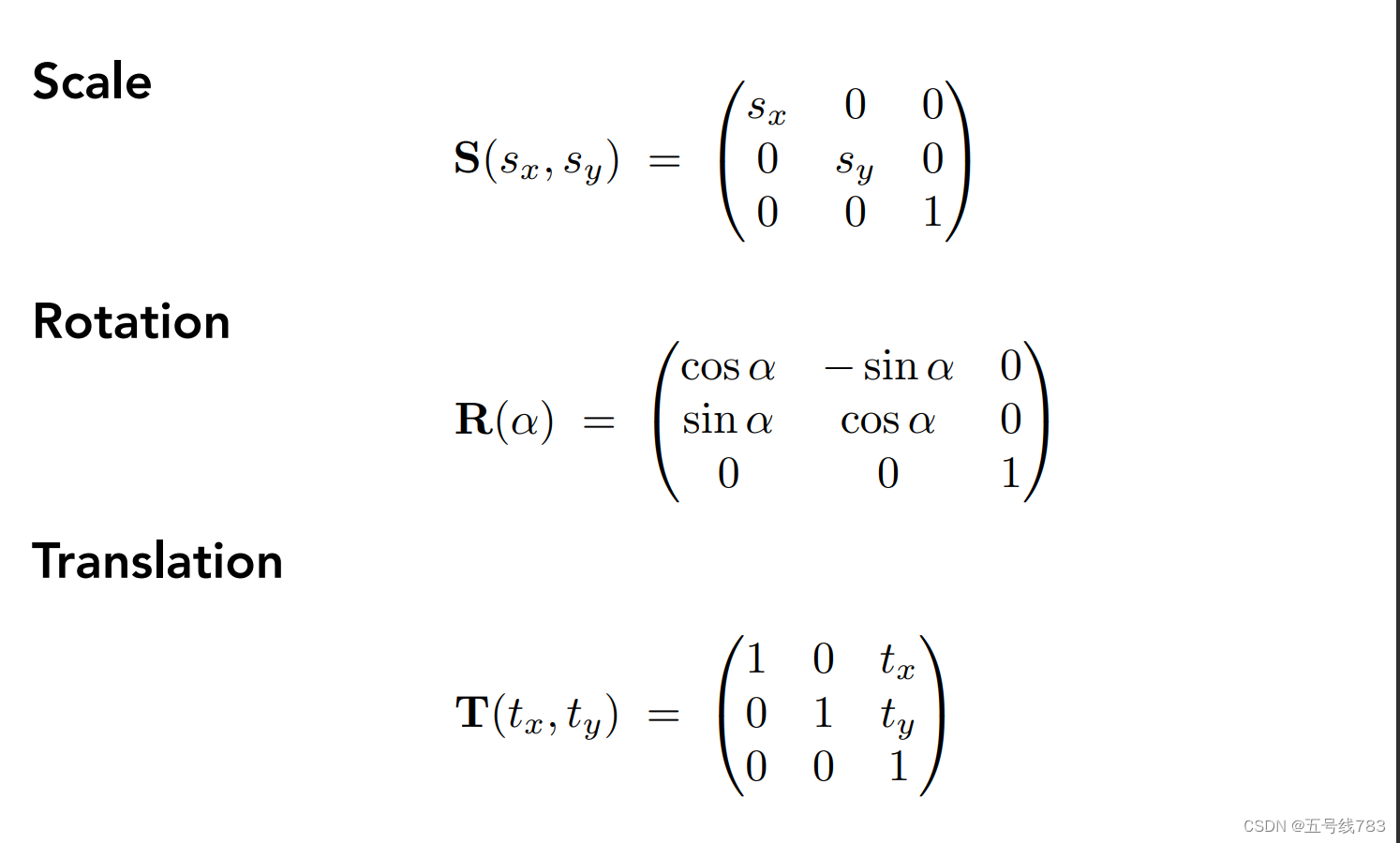
在三维的变换中，也是同样的道理

之后我们通过一个4X4的矩阵就可以表达三维世界中物体的变换了，先应用线性变换再加上位移

三维世界中的旋转比较复杂，我们先按照简单的来，根据轴的旋转，其实更具轴的旋转我们就可以简单的看为轴上的值不变，其它两轴为旋转向量，其中Y轴方向的旋转向量为何不同，这是因为Y轴是由Z轴叉乘X轴得来的，反过来了

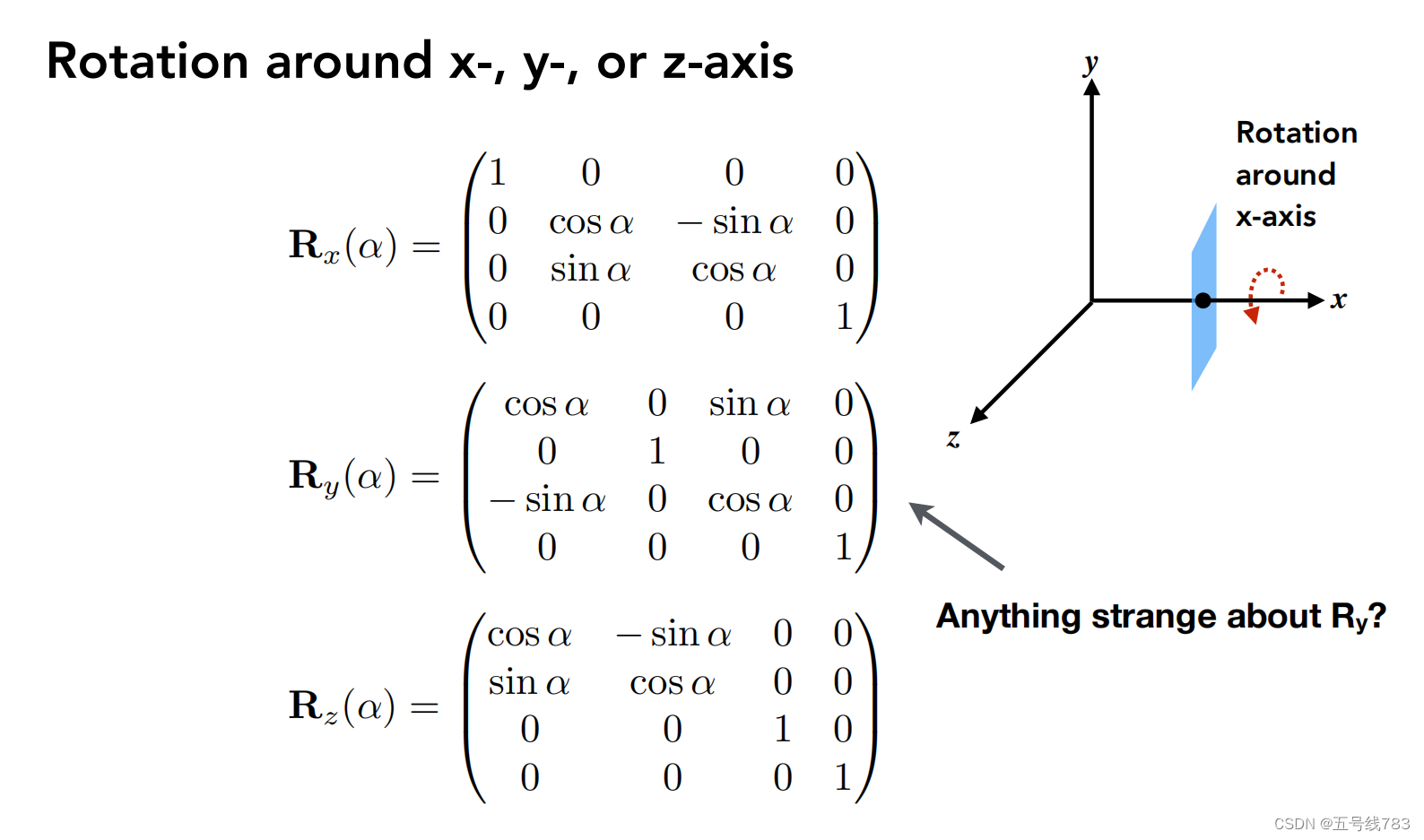那么将这个旋转扩展到整个三维空间中应该怎么做呢，简单来说就是绕任何轴的旋转都可以分解成三个轴的旋转，但是要怎么分解是一个难题，首先我们需要证明任意一个方向的旋转和以被三个轴旋转的方向所表示，实际上这是可行的，例如一个飞机的旋转，用欧拉角可以用来表示

最后在数学上，人们得到了一个公式用来表示任意一个旋转，这个旋转公式叫做罗得里格斯公式，这个公式由角度和旋转轴构成，这个旋转轴我们默认其过了原点 ，这样的话我们就可以在旋转之前先将旋转轴和物体移动到原点，然后再旋转然后再移回去，这里的N矩阵就是叉乘的矩阵表示

四元数这里不细说，我们只需要知道四元数是用来做插值的，因为例如旋转15度和旋转25度有两个矩阵表示，我将其加起来平均肯定不代表这个旋转矩阵表示旋转20度，因此引入了四元数的概念

视图变换

我们的目的是为了将三维的物体变成二维的图片，首先我们需要规定场景，那就是模型和场景的放置（model transformation），摄像机的位置方向（view transformation），最后是投影灯到相机上（projection transform），合起来成为MVP变换

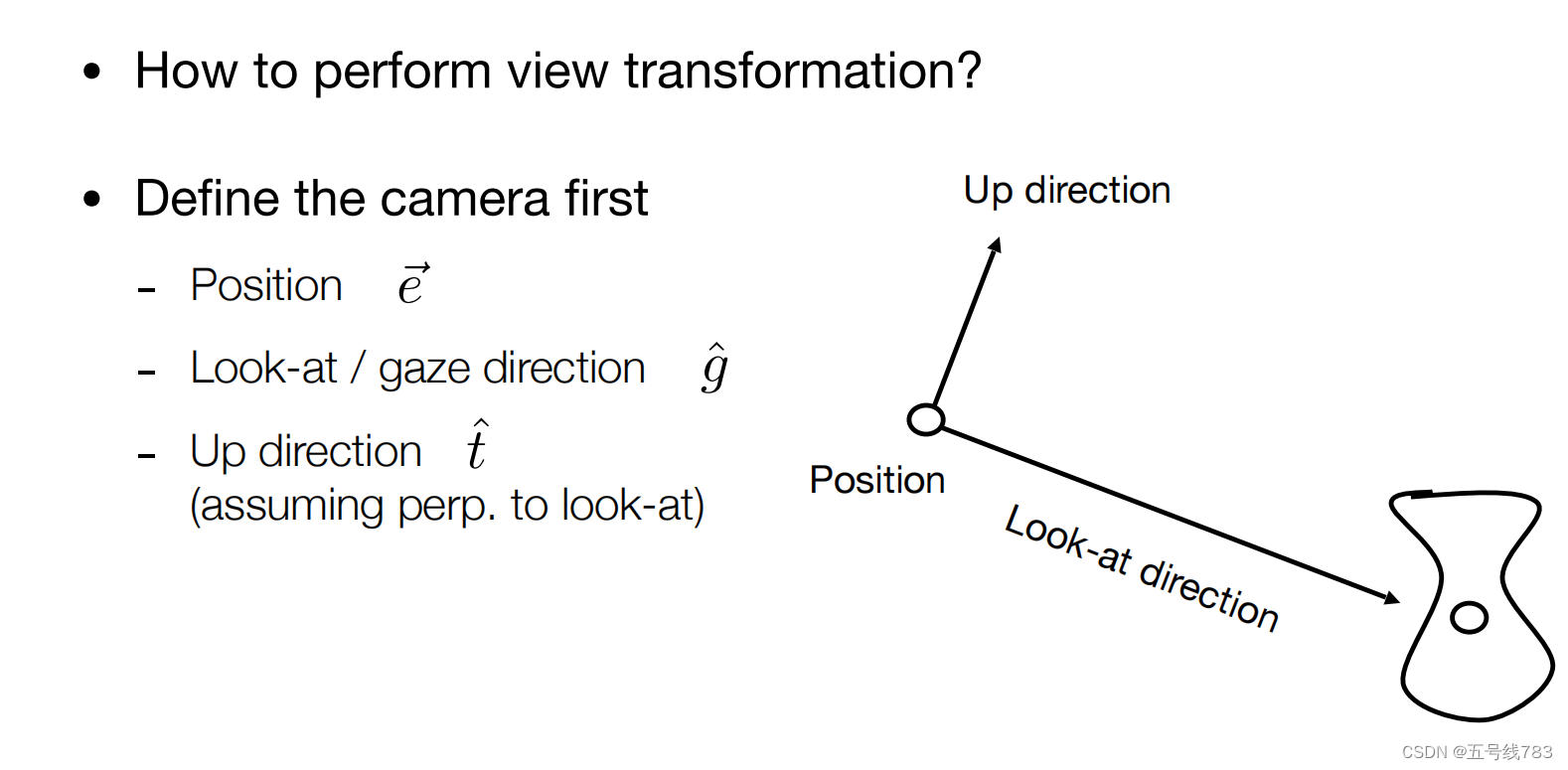
怎么做视图变换，也就是怎么摆放摄像机，包括摆放位置（position），朝向（look—at direction），以及一个向上的方向（Up direction）

我们知道，物体之间的运动表示为相对运动，那么我们为了简化计算，我们可以规定，相机永远不动，都是其它物体相对于相机运动，相机永远处在原点位置，朝向Z轴的负方向，向上的方向为Y轴

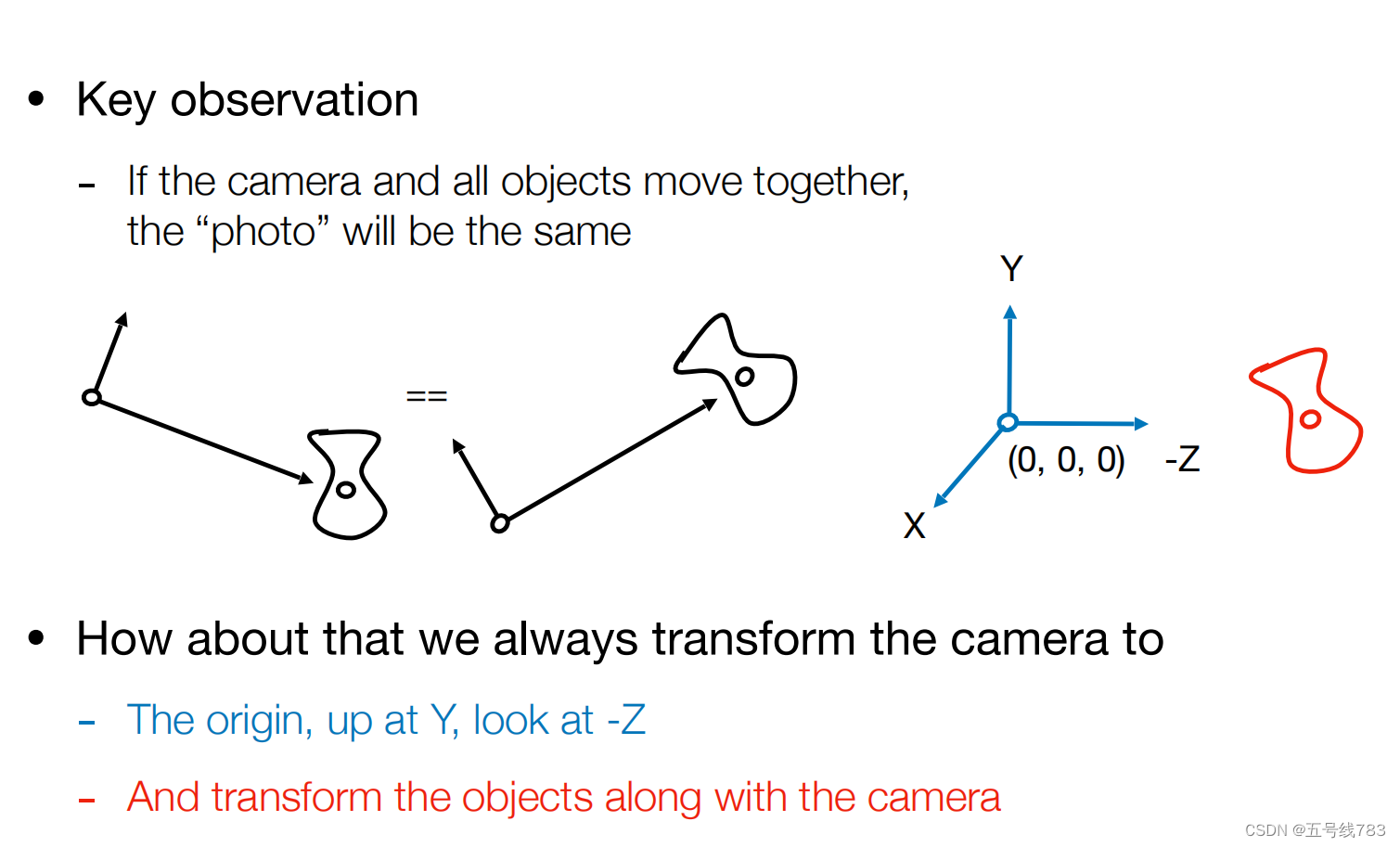
为了达成这个目标，我们需要一一对应摆放好摄像机

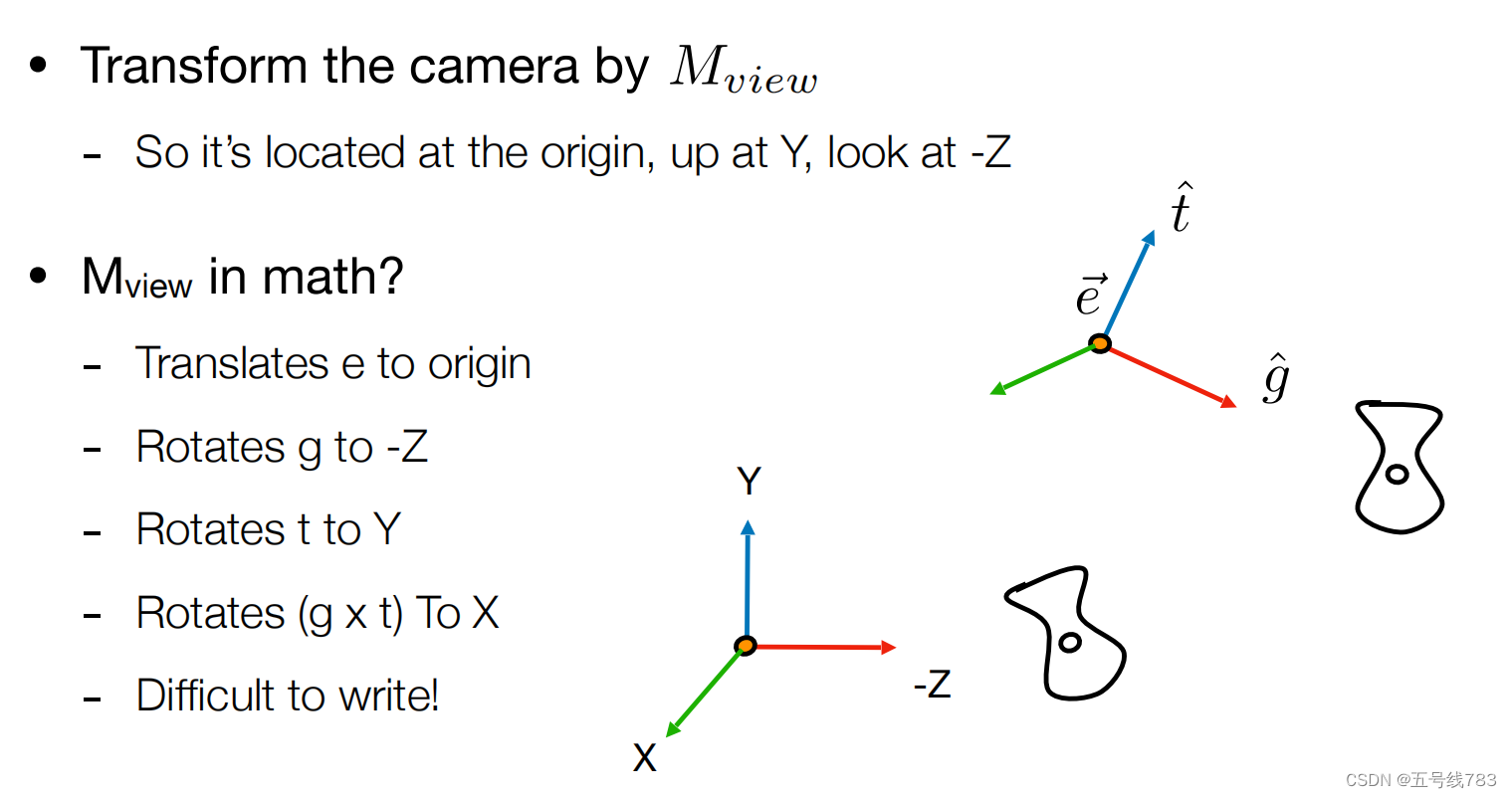
这样一系列的操作，通过几个矩阵表示，位移好写，但是旋转不好写，但同时反过来更好写，那么写出来逆矩阵再求逆矩阵就好了

同时旋转矩阵式是正交矩阵，那么直接写一个转置矩阵就好了，视图矩阵和模型矩阵本质上做的东西都是差不多的

投影变换

投影有两种不同的方法，分别是正交投影和透视投影，我们的视觉是透视投影，是否有近大远小的性质就是这两者的最大区别

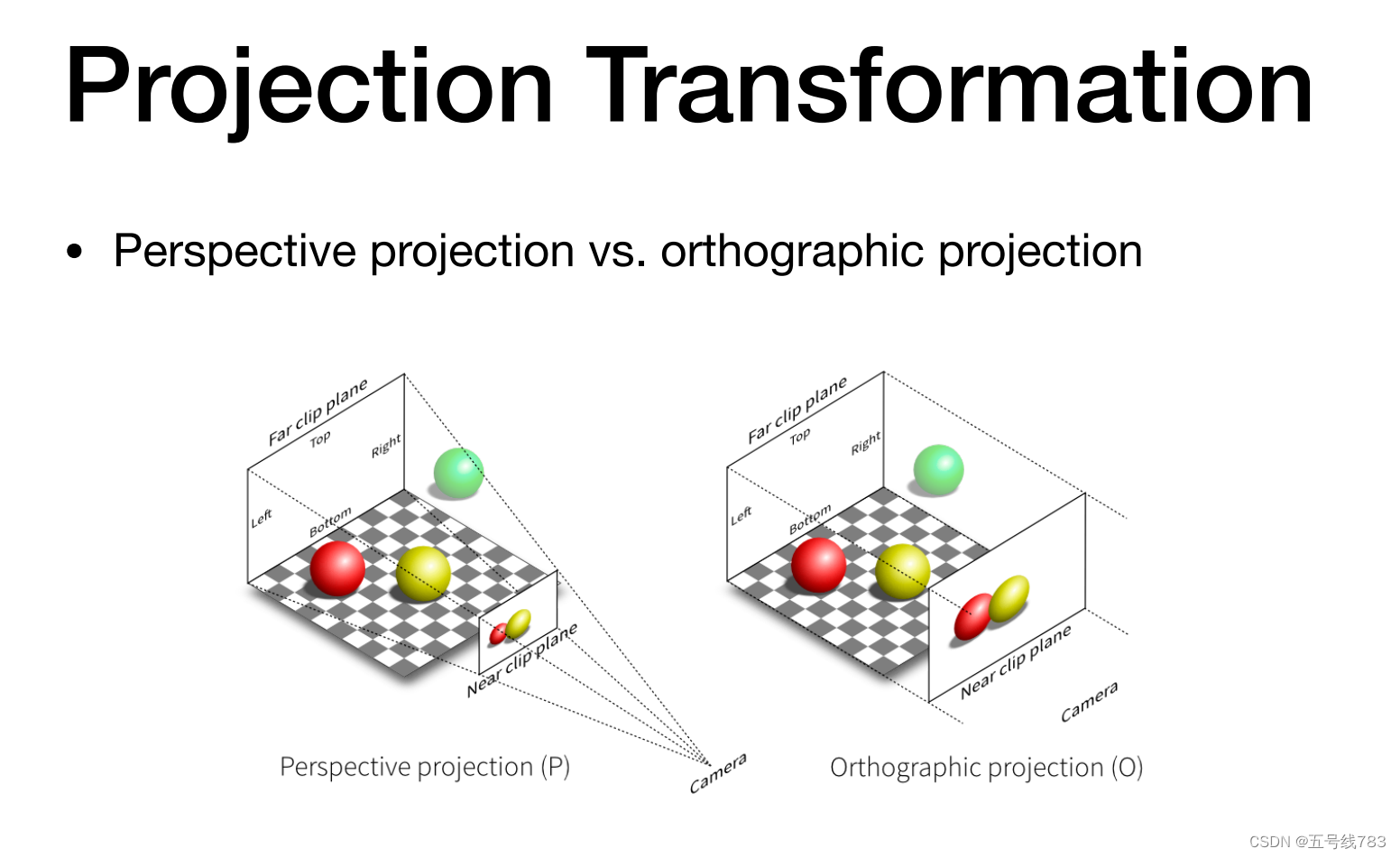
正交投影

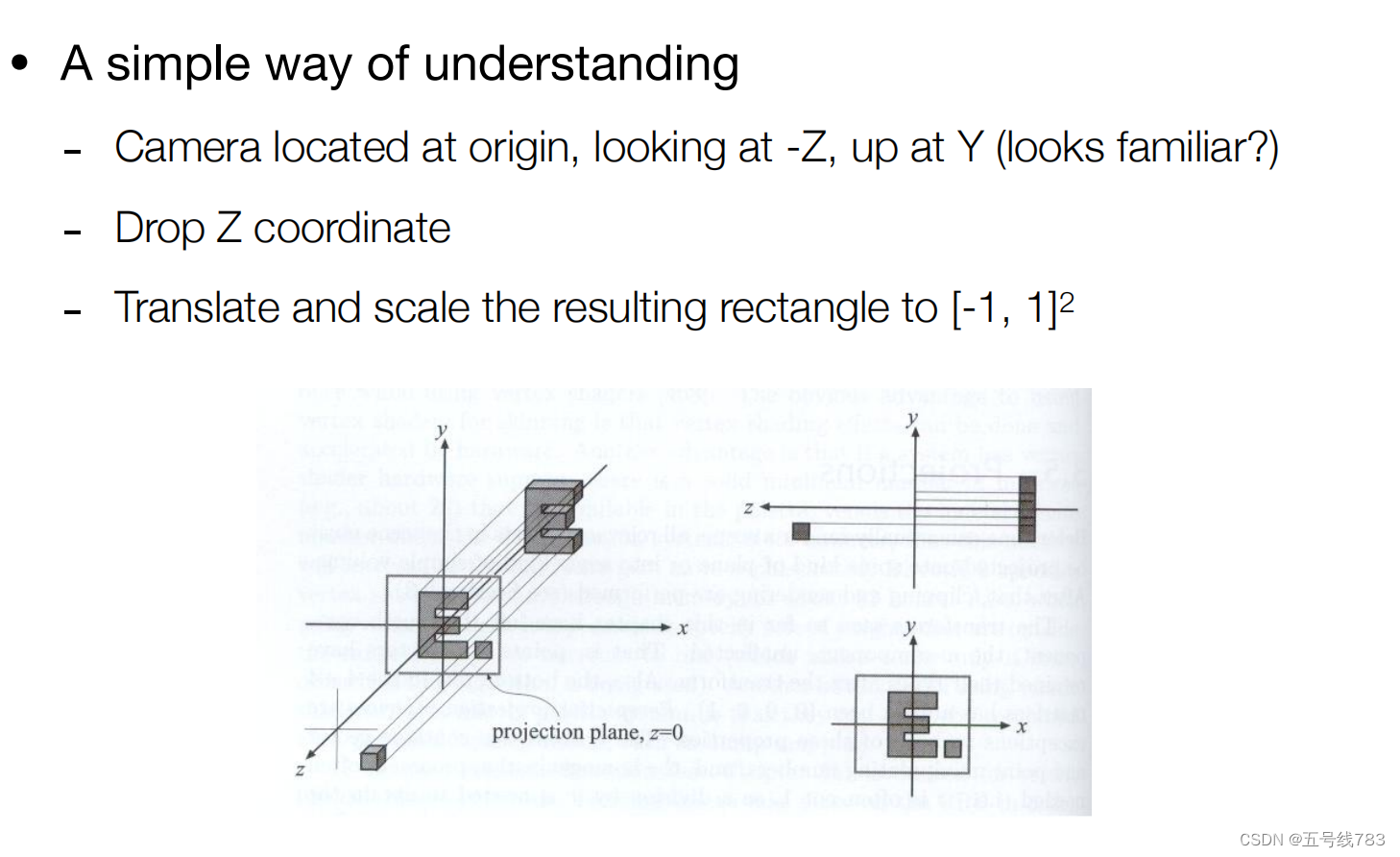
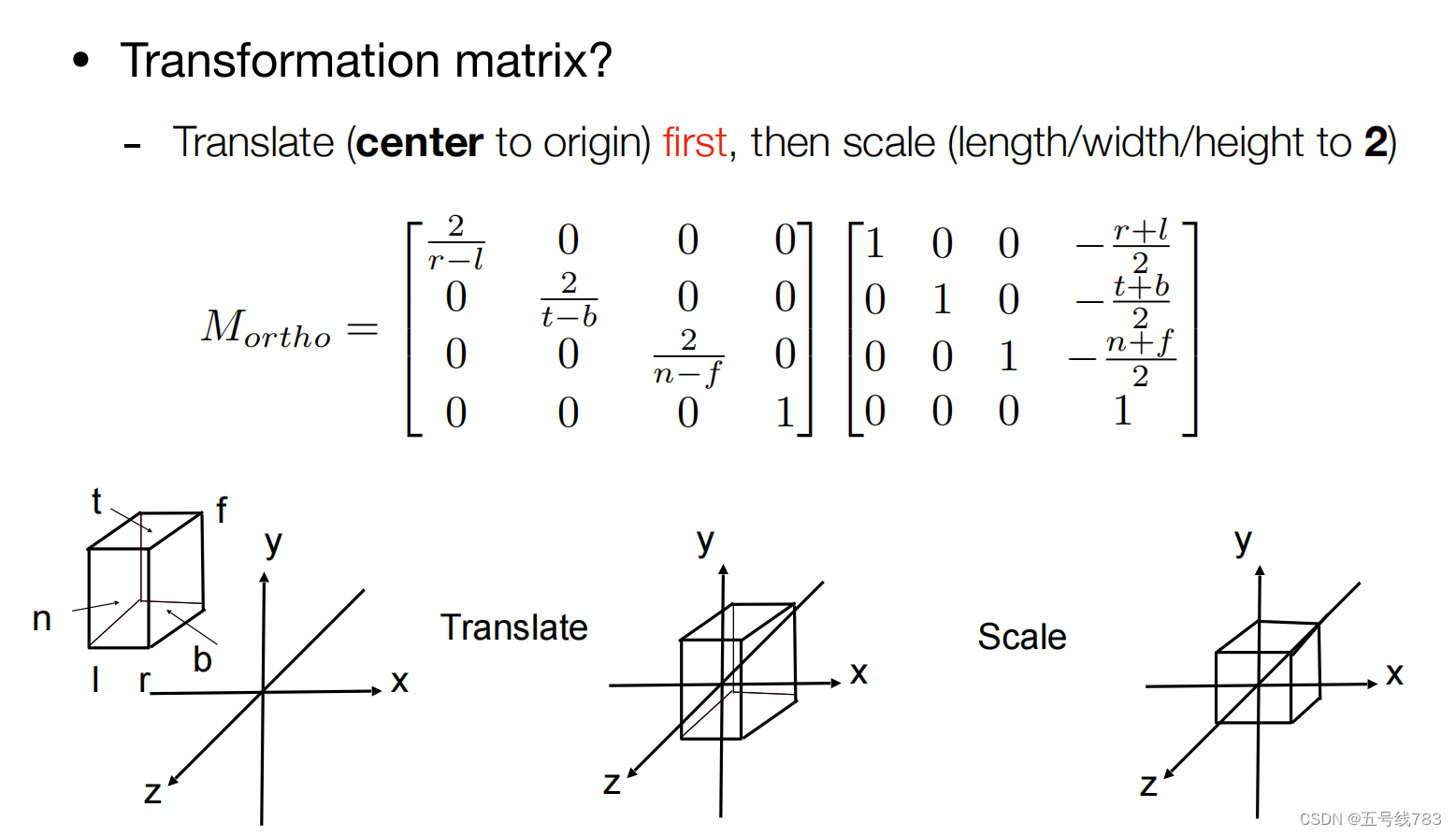
这个投影很简单，简单理解就是我们定好摄像机的位置后，抛弃掉Z轴，将所有的图形放在XY平面上，并将其缩放到-1,1的这样一个矩形上就可以了

在图形学中的做法是，我们将一个三维世界中的物体用一个长方体包起来，分别定义其X轴上的左和右，Y轴方向上的下和上，以及Z轴上的远和近，然后将整个立方体移动到以原点为中心的地方，再将其缩放成一个标准的【-1，1】^3的立方体就可以了

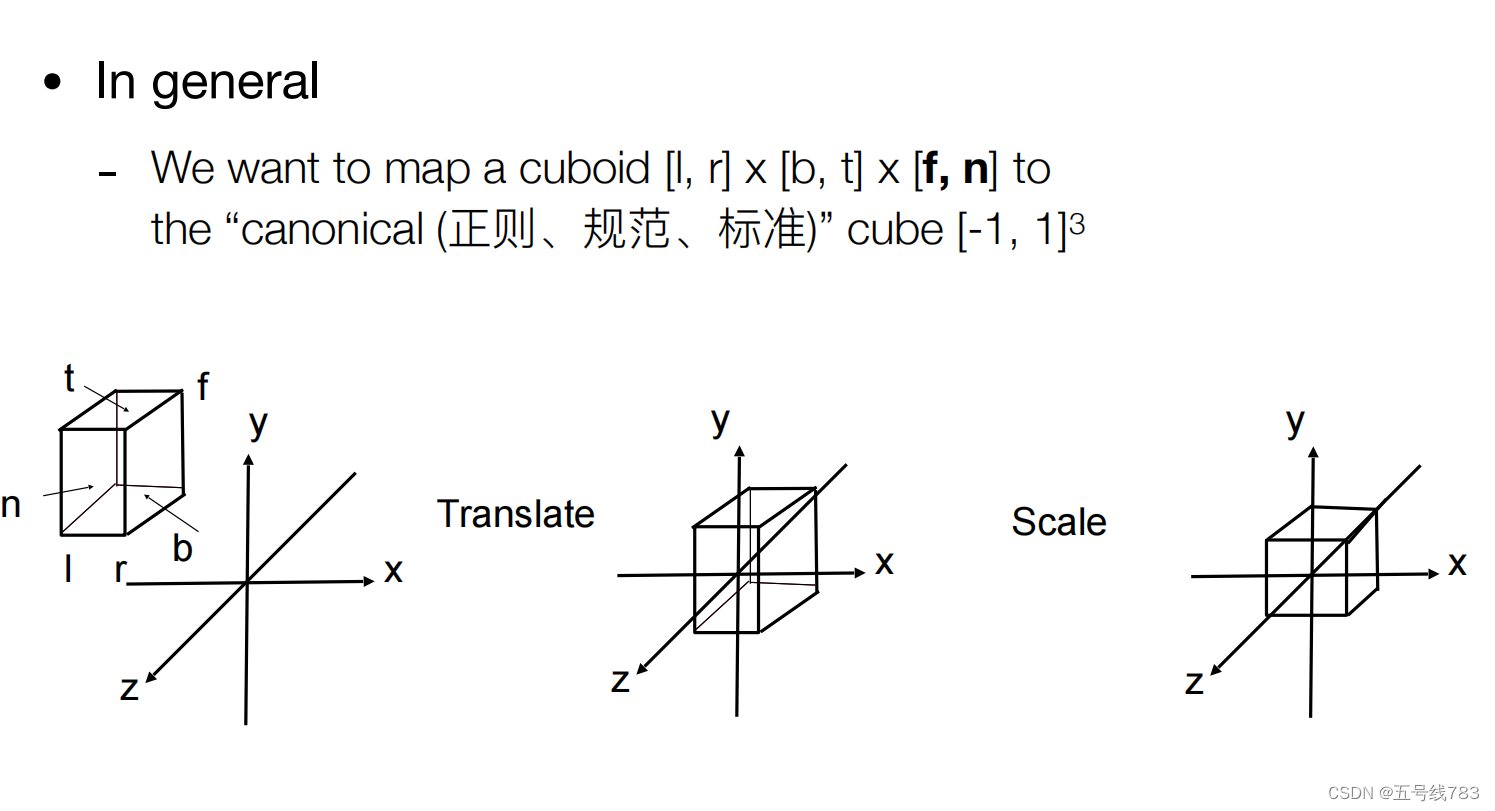
怎么写成数学上的形式呢，非常直观，一个平移一个缩放

透视投影

这个透视投影使用的更加普遍，在透视投影中，两条平行的线是会相交的

在学习透视投影前，我们需要复习一个概念，就是只要在齐次坐标中，最后一个维度的数字不为0，那么这个永远都是代表空间中的一个点

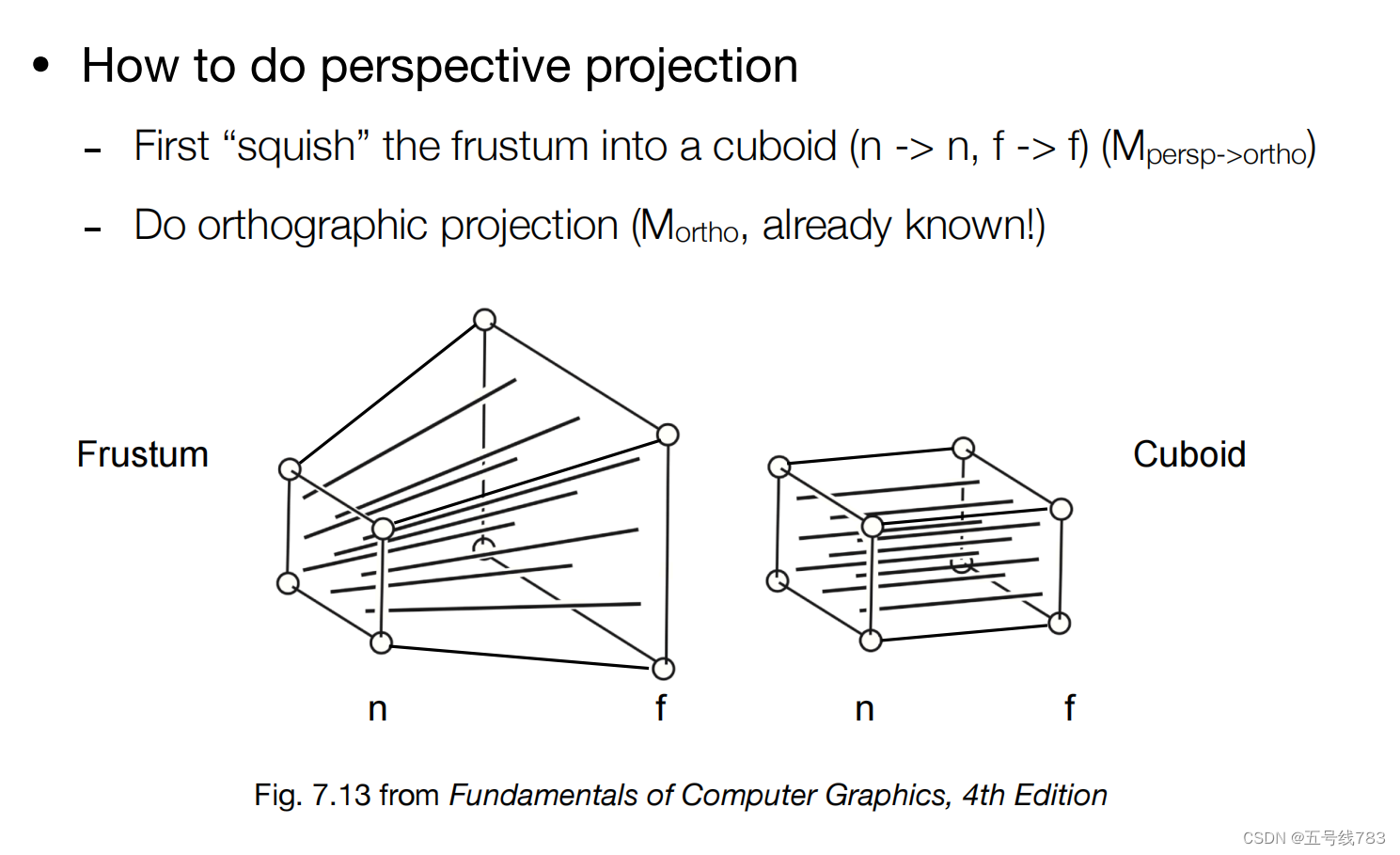
我们做透视投影的时候，可以先将透视投影中的那个原平面的平面先缩放成一个和近平面一样的大小的矩形，那这样我们就得到了一个长方体，之后拿这个长方体做一次正交投影就可以了，那么相较于正交投影，我们需要做到的就是一步从投影到正交，挤压的一个过程，这个过程也是一个变化矩阵

我们为了得到唯一的一个挤压结果，需要定义一下，首先是近平面永远不变，远平面的z值不变，远平面的中心点在挤压前后不变

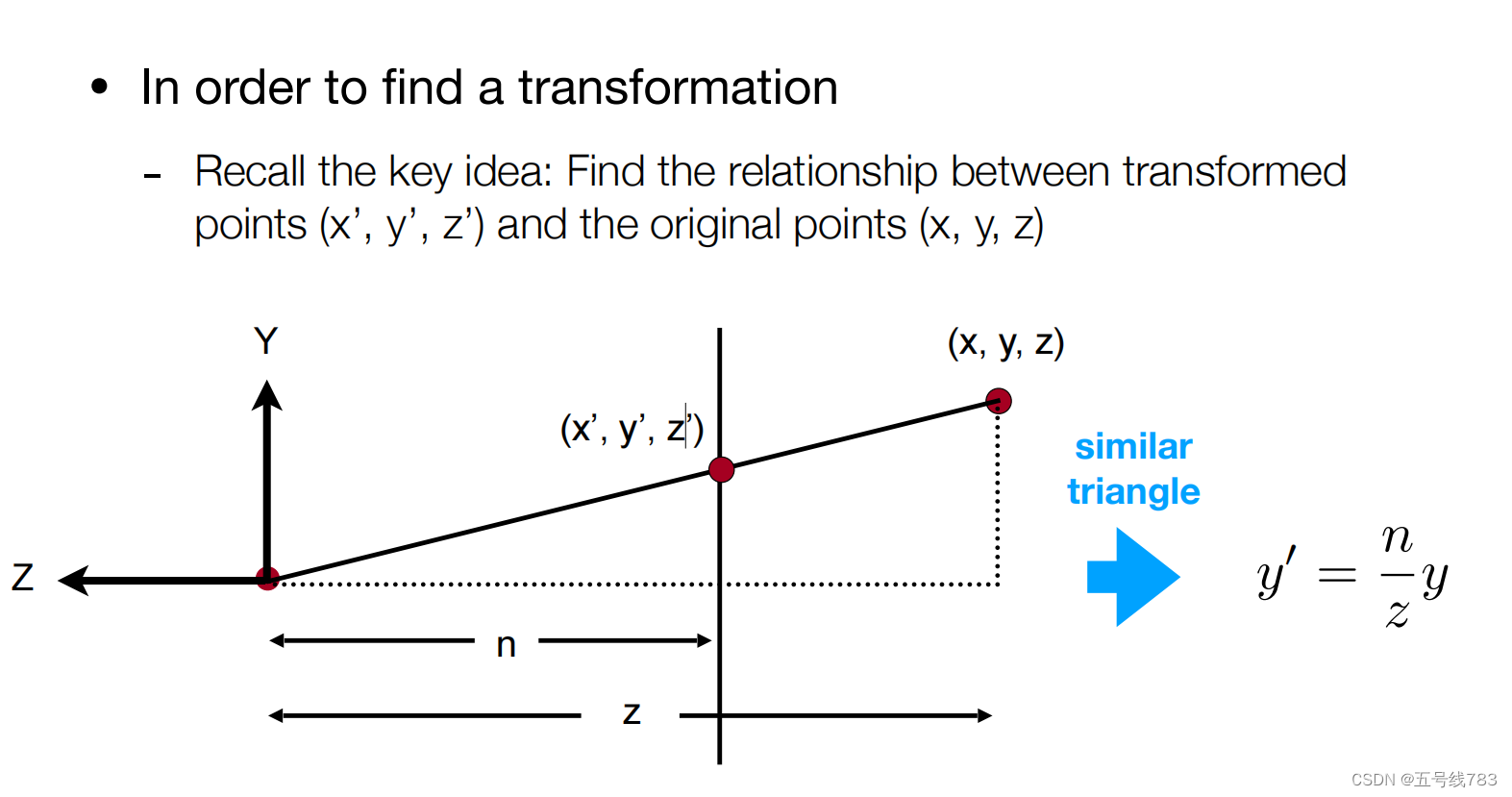
我们通过从侧面看，通过相似三角形可以得到y之间的关系

y之间的关系清楚之后，同样的我们也可以获得x之间的关系，无非就是将侧视图换成俯视图，那么在得到两个点y和x的关系之后，我们可以知道这个挤压变换矩阵乘以任意一个点可以得到的新的坐标中，x和y已经确定了

那么根据已知的信息，我们已经可以获得这个变化矩阵大部分的值了

我们就只需要再求出第三行，这时候需要利用到两个条件，第一个条件，在近平面上变换后所有的点不变，在远平面上所有的点变换后z不变

代入两个条件，第一个条件近处平面，那么我们可以知道第三行前两个数为0，因为结果的第三行一列的数字为n，和xy没有关系

带入第二个条件，远平面的定义，我们取远平面的中心点（0,0，f，1）那么结合刚刚的等式，我们可以得到两个等式

根据这两个等式我们就可以得出A和B

最后我们要明白中间的Z在经过挤压变化的时候是会变化的，应该是边近了，因为投影的线会变短