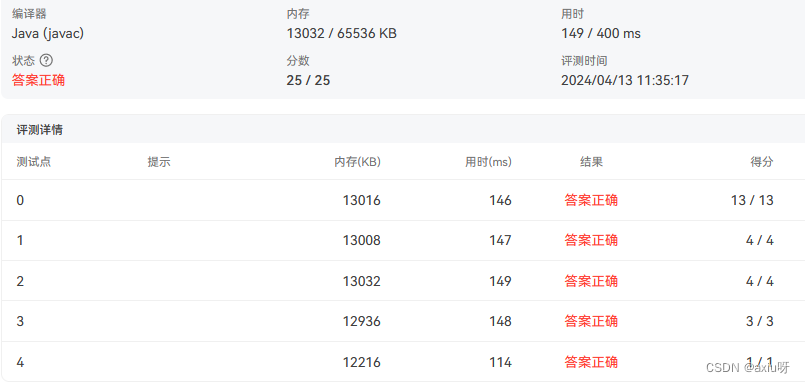
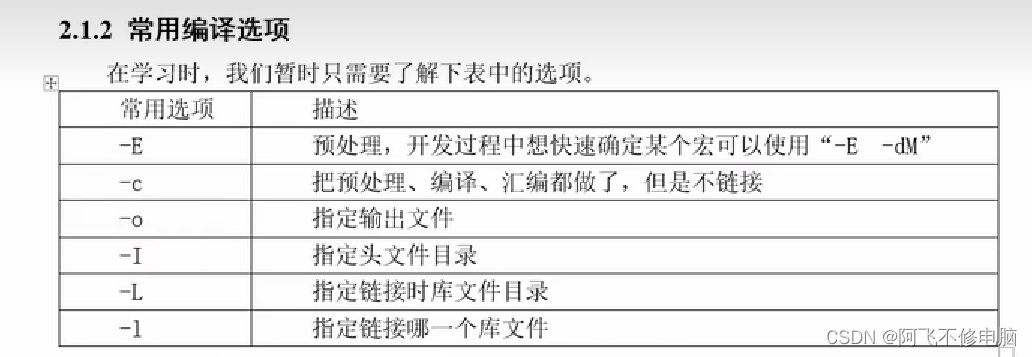
01-数据结构—判断题
02-数据结构—选择题
03 数据结构—多选+填空+程序填空
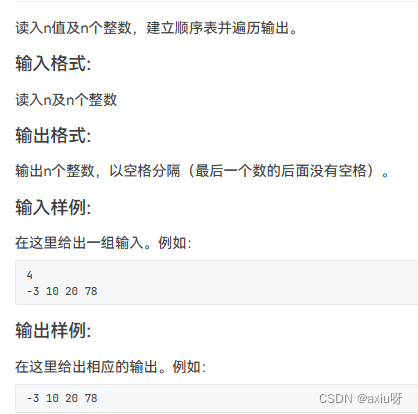
01-顺序表的建立及遍历
import java.util.Iterator;
import java.util.LinkedList;
import java.util.ListIterator;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
// 输出n个整数，以空格分隔（最后一个数的后面没有空格）
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
int[] arr = new int[num];
// 创建一个空的链表
LinkedList<Integer> numbers = new LinkedList<>();
for (int i = 0; i < num; i++) {
numbers.add(sc.nextInt());
}
ListIterator<Integer> iterator = numbers.listIterator();
boolean isFirst = true;
while (iterator.hasNext()) {
//不是第一个元素就打印空格
if (!isFirst) {
System.out.print(" ");
} else {
isFirst = false;
}
System.out.print(iterator.next());
}
}
}
02-递增有序顺序表的插入
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
// 第1行输入顺序表长度，第2行输入递增有序的顺序表，第3行输入要插入的数据元素X。
// 对每一组输入，在一行中输出插入X后的递增的顺序表。
Scanner sc = new Scanner(System.in);
int length = sc.nextInt();
int arr[] = new int[length+1];
for (int i = 0; i < length; i++) {
arr[i] = sc.nextInt();
}
int num = sc.nextInt();
arr[length] = num;
int j = 0;
for (int i = length; i > 0; i--) {
if (arr[i]<arr[i-1]) {
j=arr[i];
arr[i] = arr[i-1];
arr[i-1]=j;
}
}
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i]+",");
}
}
}
03-顺序表的插入
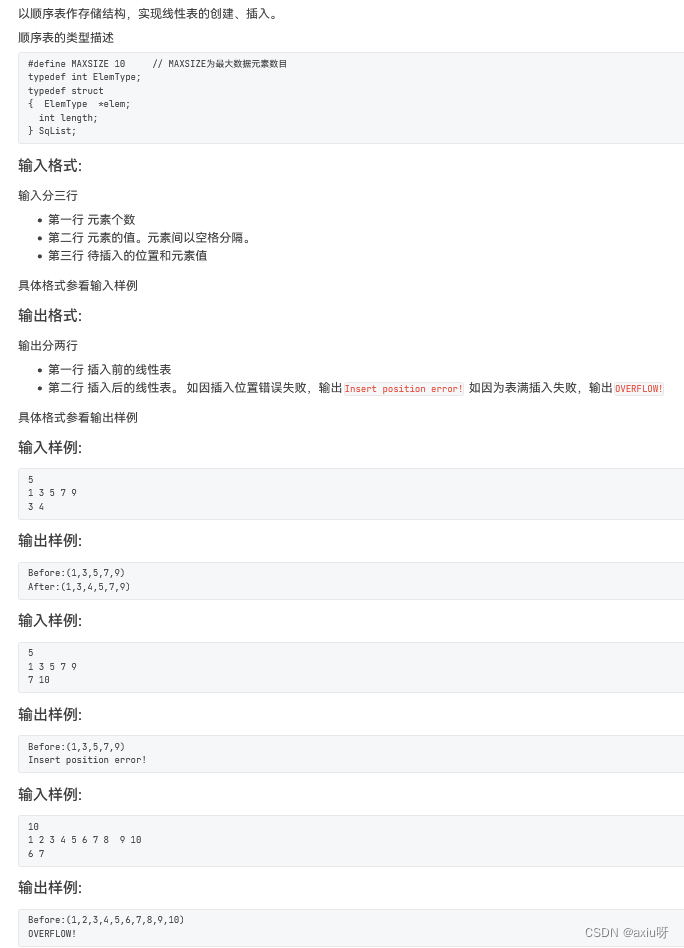
import java.util.Scanner;
public class Main {
// MAXSIZE为最大数据元素数目
private static final int MAXSIZE = 10;
// 定义顺序表结构
static class SqList {
ElemType[] elem;
int length;
// 构造函数初始化
@SuppressWarnings("unchecked")
public SqList(int size) {
elem = new ElemType[size];
length = 0;
}
}
// 定义元素类型
static class ElemType {
int value;
public ElemType(int value) {
this.value = value;
}
}
// 创建顺序表
public static SqList createList(int n, int[] values) {
SqList list = new SqList(MAXSIZE);
for (int i = 0; i < n; i++) {
list.elem[i] = new ElemType(values[i]);
}
list.length = n;
return list;
}
// 插入元素
public static String insertElem(SqList list, int position, int value) {
if (list.length == MAXSIZE) {
return "OVERFLOW!";
}
if (position < 1 || position > list.length + 1) {
return "Insert position error!";
}
for (int i = list.length; i >= position; i--) {
list.elem[i] = list.elem[i - 1];
}
list.elem[position - 1] = new ElemType(value);
list.length++;
return null;
}
// 打印顺序表
public static String printList(SqList list) {
StringBuilder sb = new StringBuilder();
sb.append("(");
for (int i = 0; i < list.length; i++) {
sb.append(list.elem[i].value);
if (i < list.length - 1) {
sb.append(",");
}
}
sb.append(")");
return sb.toString();
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 读取输入
int n = scanner.nextInt();
int[] values = new int[n];
for (int i = 0; i < n; i++) {
values[i] = scanner.nextInt();
}
int position = scanner.nextInt();
int value = scanner.nextInt();
// 创建顺序表
SqList list = createList(n, values);
// 打印插入前的顺序表
System.out.println("Before:" + printList(list));
// 插入元素并打印插入后的顺序表或错误信息
String result = insertElem(list, position, value);
if (result == null) {
System.out.println("After:" + printList(list));
} else {
System.out.println(result);
}
}
}
04-数据结构实验一 顺序表的删除
import java.util.Scanner;
public class Main {
// MAXSIZE为最大数据元素数目
private static final int MAXSIZE = 10;
// 定义顺序表结构
static class SqList {
ElemType[] elem;
int length;
// 构造函数初始化
@SuppressWarnings("unchecked")
public SqList(int size) {
elem = new ElemType[size];
length = 0;
}
}
// 定义元素类型
static class ElemType {
int value;
public ElemType(int value) {
this.value = value;
}
}
// 创建顺序表
public static SqList createList(int n, int[] values) {
SqList list = new SqList(MAXSIZE);
for (int i = 0; i < n; i++) {
list.elem[i] = new ElemType(values[i]);
}
list.length = n;
return list;
}
// 删除元素
public static String deleteElem(SqList list, int position) {
if (position < 1 || position > list.length) {
return "Delete position error!";
}
for (int i = position - 1; i < list.length - 1; i++) {
list.elem[i] = list.elem[i + 1];
}
list.elem[list.length - 1] = null; // 清除最后一个元素
list.length--;
return null;
}
// 打印顺序表
public static String printList(SqList list) {
StringBuilder sb = new StringBuilder();
sb.append("(");
for (int i = 0; i < list.length; i++) {
sb.append(list.elem[i].value);
if (i < list.length - 1) {
sb.append(",");
}
}
sb.append(")");
return sb.toString();
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 读取输入
int n = scanner.nextInt();
int[] values = new int[n];
for (int i = 0; i < n; i++) {
values[i] = scanner.nextInt();
}
int position = scanner.nextInt();
// 创建顺序表
SqList list = createList(n, values);
// 打印删除前的顺序表
System.out.println("Before:" + printList(list));
// 删除元素并打印删除后的顺序表或错误信息
String result = deleteElem(list, position);
if (result == null) {
System.out.println("After:" + printList(list));
} else {
System.out.println(result);
}
}
}
05-哈夫曼树
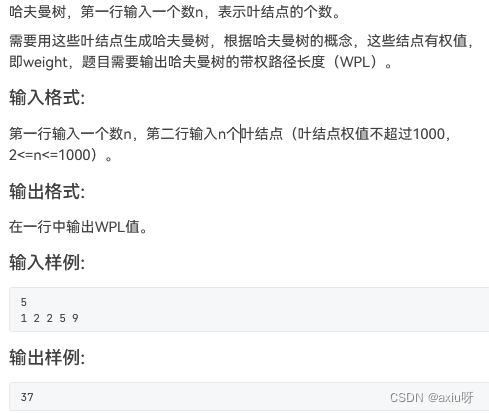
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
// 读取叶子结点的个数
int n = sc.nextInt();
// 读取每个叶子结点的权值
int[] weights = new int[n];
for (int i = 0; i < n; i++) {
weights[i] = sc.nextInt();
}
sc.close();
//构造哈夫曼树
HuffmanTree tree = buildHuffmanTree(weights);
//获取哈夫曼树的带权路径长度
int wpl = tree.getWPL();
//输出带权路径长度
System.out.println(wpl);
}
//构建哈夫曼树
private static HuffmanTree buildHuffmanTree(int[] weights) {
//使用优先队列存储节点，按照权值从小到大排序
PriorityQueue<HuffmanTree.Node> priorityQueue = new PriorityQueue<>(Comparator.comparingInt(node -> node.weight));
//将每个叶子结点添加到优先队列中
for (int weight : weights) {
priorityQueue.offer(new HuffmanTree.Node(weight));
}
//不断地从优先队列中取出权值最小的两个结点，合并成一个新的父节点，直到只剩一个节点为止
while (priorityQueue.size() > 1) {
HuffmanTree.Node left = priorityQueue.poll();
HuffmanTree.Node right = priorityQueue.poll();
HuffmanTree.Node parent = new HuffmanTree.Node(left.weight + right.weight);
parent.left = left;
parent.right = right;
priorityQueue.offer(parent);
}
return new HuffmanTree(priorityQueue.poll());
}
static class HuffmanTree{
private Node root;
//构造函数，根据根节点创建哈夫曼树
public HuffmanTree(Node root) {
this.root = root;
}
//获取哈夫曼树的带权路径长度
public int getWPL() {
return calculateWPL(root,0);
}
//递归计算哈夫曼树的带权路径长度
private int calculateWPL(Node node, int depth) {
if (node == null) {
return 0;
}
//如果是叶子节点，返回权值乘以深度
if (node.left == null && node.right == null) {
return node.weight * depth;
}
//非叶子结点，继续递归计算左右子树的带权路径长度
return calculateWPL(node.left, depth+1)+calculateWPL(node.right, depth+1);
}
//结点类
static class Node{
int weight; //权值
Node left; // 左孩子
Node right; //右孩子
//构造函数，创建具有指定权值的叶子结点
public Node(int weight) {
this.weight = weight;
}
}
}
}
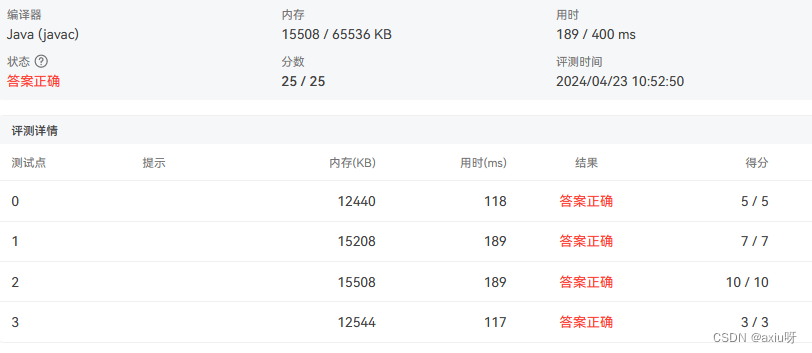
06-还原二叉树
import java.util.Scanner;
public class Main {
// 定义二叉树节点
static class TreeNode {
char val;
TreeNode left;
TreeNode right;
TreeNode(char x) {
val = x;
}
}
// 根据前序和中序遍历序列构建二叉树
public static TreeNode buildTree(char[] preorder, char[] inorder) {
return buildTreeHelper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
}
private static TreeNode buildTreeHelper(char[] preorder, int preStart, int preEnd,
char[] inorder, int inStart, int inEnd) {
if (preStart > preEnd || inStart > inEnd) {
return null;
}
char rootVal = preorder[preStart];
TreeNode root = new TreeNode(rootVal);
int rootIndex = 0;
for (int i = inStart; i <= inEnd; i++) {
if (inorder[i] == rootVal) {
rootIndex = i;
break;
}
}
int leftTreeSize = rootIndex - inStart;
root.left = buildTreeHelper(preorder, preStart + 1, preStart + leftTreeSize,
inorder, inStart, rootIndex - 1);
root.right = buildTreeHelper(preorder, preStart + leftTreeSize + 1, preEnd,
inorder, rootIndex + 1, inEnd);
return root;
}
// 计算二叉树的高度
public static int treeHeight(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = treeHeight(root.left);
int rightHeight = treeHeight(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 读取输入
int n = scanner.nextInt();
String preorderStr = scanner.next();
String inorderStr = scanner.next();
char[] preorder = preorderStr.toCharArray();
char[] inorder = inorderStr.toCharArray();
// 构建二叉树
TreeNode root = buildTree(preorder, inorder);
// 计算二叉树的高度
int height = treeHeight(root);
// 输出结果
System.out.println(height);
}
}
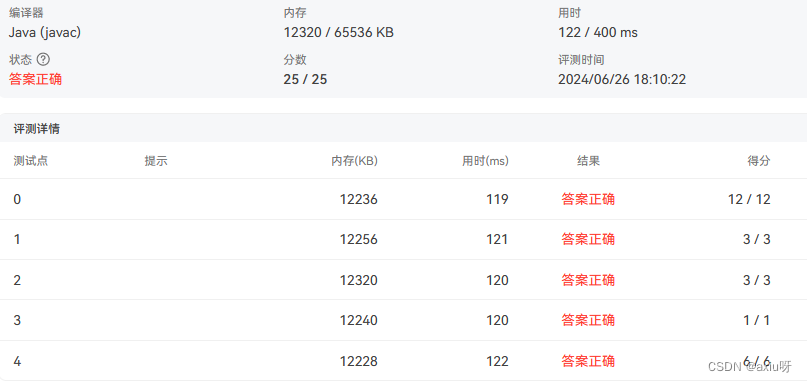07-玩转二叉树
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Main {
static int n;
static int[]id;
static int[]pr;
static Queue<node>q=new LinkedList<node>();
public static node build(int prl,int prr,int il,int ir) {
if(il>ir) return null;
node root=new node();
int v=pr[prl];
root.v=v;
int i;
for(i=il;i<=ir;i++)if(id[i]==v)break;
int num=i-il;
//镜面反转，是指将所有非叶结点的左右孩子对换
//把比根节点大的建在根节点的左边，比根节点小的建在根节点的右边
root.le=build(prl+num+1,prr,i+1,ir);
root.ri=build(prl+1,prl+num,il,i-1);
return root;
}
public static void print() {
int t=1;
while(!q.isEmpty()) {
node r=q.poll();
if(t==n)System.out.println(r.v);
else {
System.out.print(r.v+" ");
t++;
}
if(r.le!=null)q.add(r.le);
if(r.ri!=null)q.add(r.ri);
}
}
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
n=in.nextInt();
id=new int[n+1];
pr=new int[n+1];
for(int i=1;i<=n;i++)id[i]=in.nextInt();
for(int i=1;i<=n;i++)pr[i]=in.nextInt();
node root=build(1,n,1,n);
q.add(root);
print();
}
}
class node{
int v;
node le;
node ri;
}
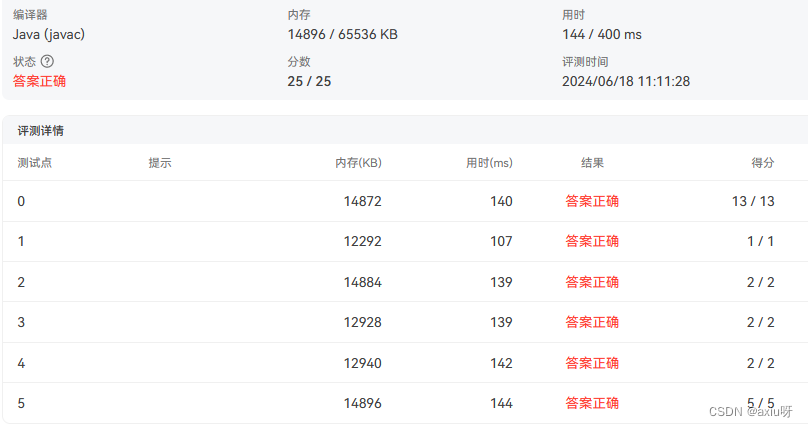
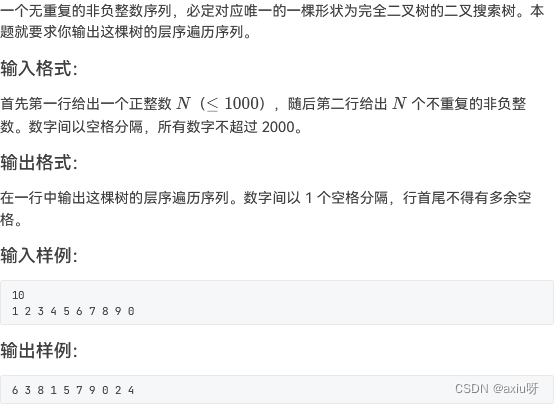
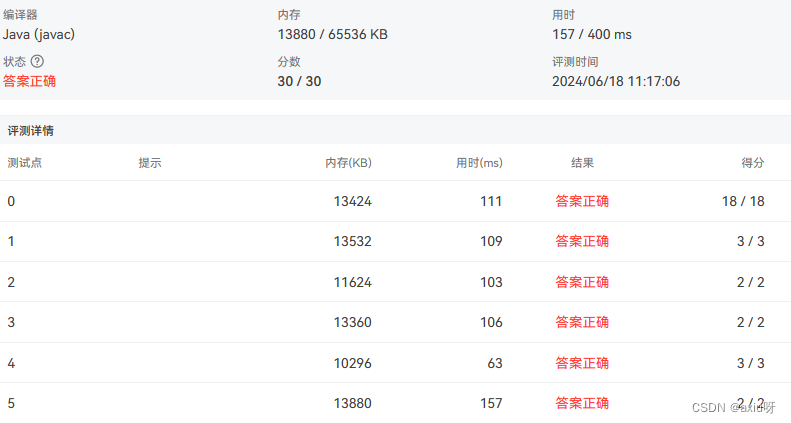
08-完全二叉搜索树
import java.io.*;
import java.util.Arrays;
public class Main {
static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
public static int ini() throws IOException {
st.nextToken();
return (int)st.nval;
}
static int n, idx;
static int []tree;
static int []arr;
public static void main(String[] args) throws NumberFormatException, IOException {
n = ini();
arr = new int[n];
tree = new int[n + 1];
for(int i = 0; i < n; i++) arr[i] = ini();
Arrays.sort(arr);
build(1);
System.out.print(tree[1]);
for(int i = 2; i <= n; i++) System.out.print(" " + tree[i]);
}
public static void build(int root) {
if(root * 2 <= n) build(root * 2);
tree[root] = arr[idx++];
if(root *2 + 1 <= n) build(root * 2 + 1);
}
} 
09-是否完全二叉搜索树
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
Reader.init(System.in);
N = Reader.nextInt();
int[] tree = new int[4194303];
/*
* fa = (child - 1) / 2 left_child = (fa + 1) * 2 - 1 right_child = (fa + 1) * 2
*/
for (int i = 0; i < N; i++) {
int node = Reader.nextInt();
insert(tree, node);
}
show(tree);
if(isOK) {
System.out.println("YES");
}else {
System.out.println("NO");
}
}
static int N;
static boolean isOK = true;
static void insert(int[] tree, int node) {
int current = 0;
while (tree[current] != 0) {
if (node < tree[current]) {
current = (current + 1) * 2;
} else {
current = (current + 1) * 2 - 1;
}
}
if (current >= N) {
isOK = false;
}
tree[current] = node;
}
static void show(int[] tree) {
int count = 0;
for (int i = 0; i < tree.length; i++) {
if(tree[i] != 0) {
count++;
if(count == N) {
System.out.println(tree[i]);
break;
}
System.out.print(tree[i] + " ");
}
}
}
}
// Class for buffered reading int and double values *//*
class Reader {
static BufferedReader reader;
static StringTokenizer tokenizer;
// ** call this method to initialize reader for InputStream *//*
static void init(InputStream input) {
reader = new BufferedReader(new InputStreamReader(input));
tokenizer = new StringTokenizer("");
}
// ** get next word *//*
static String next() throws IOException {
while (!tokenizer.hasMoreTokens()) {
// TODO add check for eof if necessary
tokenizer = new StringTokenizer(reader.readLine());
}
return tokenizer.nextToken();
}
static String nextLine() throws IOException {
return reader.readLine();
}
static int nextInt() throws IOException {
return Integer.parseInt(next());
}
static char nextChar() throws IOException {
return next().toCharArray()[0];
}
static float nextFloat() throws IOException {
return Float.parseFloat(next());
}
}
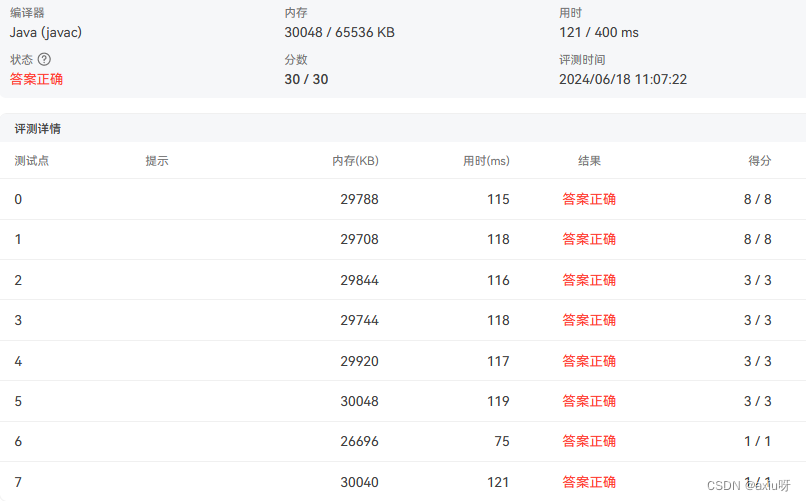
10-树的遍历
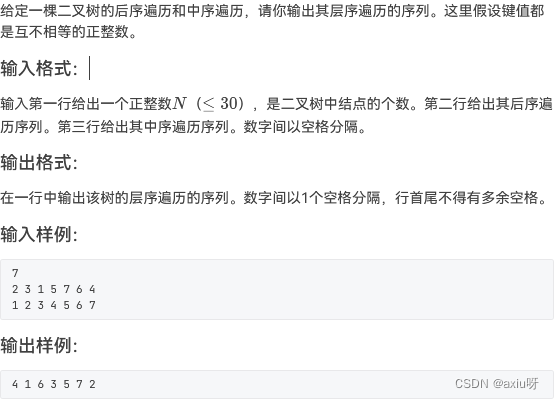
import java.util.*;
public class Main {
static int[] post = new int[35];
static int[] in = new int[35];
static int[] level = new int[10000];
// 后序中的最后一个结点是根结点 root，在中序中从 start 到 end 移动 i 找到这个根结点的位置，
// i 以左是左子树，以右是右子树
static void pre(int start, int end, int root, int index) {
if (start > end)
return; // 当一个结点就是一个树时，start==end；将这个最底层的叶子结点存入 level 后就应该结束递归了。
int i = start;
while (i < end && in[i] != post[root])
i++;
level[index] = post[root];
pre(start, i - 1, root - (end - i) - 1, index * 2 + 1);
pre(i + 1, end, root - 1, index * 2 + 2);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
for (int i = 0; i < n; i++) {
post[i] = scanner.nextInt();
}
for (int i = 0; i < n; i++) {
in[i] = scanner.nextInt();
}
pre(0, n - 1, n - 1, 0);
int cnt = 0;
for (int i = 0; i < 10000; i++) {
if (level[i] != 0 && cnt < n - 1) {
System.out.print(level[i] + " ");
cnt++;
} else if (level[i] != 0) {
System.out.print(level[i]);
break;
}
}
scanner.close();
}
}
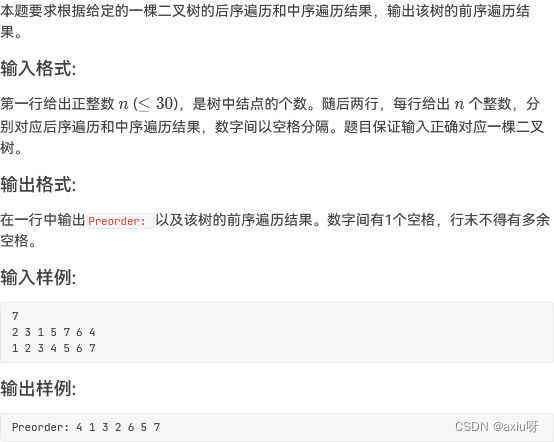
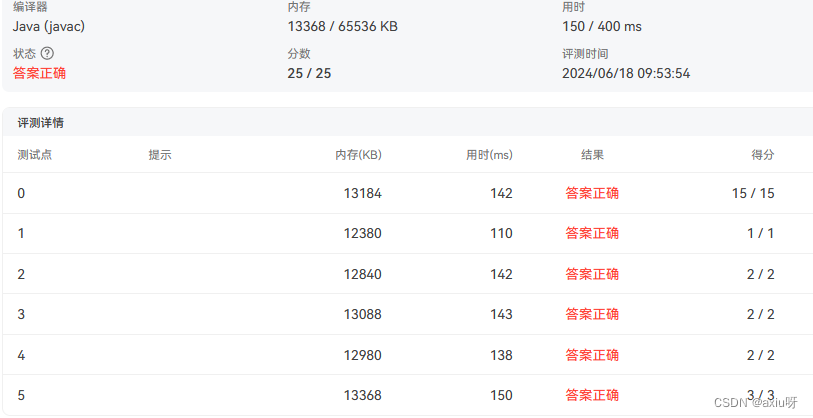11-根据后序和中序遍历输出前序遍历
import java.util.*;
class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode(int x){
val = x;
}
}
public class Main {
//根据后序和中序遍历结果构造二叉树
public static TreeNode builTree(int[] inorder,int[] postorder,int inStart,int inEnd,int postStart,int postEnd,
Map<Integer, Integer> inorderMap) {
// 边界条件：如果子区间的下标越界，说明已经到达叶子节点或者不存在合法的子树，返回null
if (inStart>inEnd || postStart>postEnd) {
return null;
}
// 后序遍历最后一个元素是当前子树的根节点
int rootval = postorder[postEnd];
TreeNode root = new TreeNode(rootval);
// 在中序遍历数组中找到当前子树根节点的位置
int rootIndex = inorderMap.get(rootval);
// 递归构建左右子树
root.left = builTree(inorder, postorder, inStart, rootIndex-1, postStart,
postStart+rootIndex-inStart-1, inorderMap);
root.right = builTree(inorder, postorder, rootIndex+1, inEnd,
postStart+rootIndex-inStart, postEnd-1, inorderMap);
return root;
}
//前序遍历二叉树
public static void preorder(TreeNode root,StringBuilder sbu) {
if (root == null) {
return;
}
sbu.append(root.val).append(" ");
preorder(root.left, sbu);
preorder(root.right, sbu);
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
int[] postorder = new int[num];
int[] inorder = new int[num];
// 后序遍历
for (int i = 0; i < num; ++i) {
postorder[i] = sc.nextInt();
}
// 中序遍历
for (int i = 0; i < num; ++i) {
inorder[i] = sc.nextInt();
}
Map<Integer, Integer> inorderMap = new HashMap<>();
for (int i = 0; i < num; i++) {
inorderMap.put(inorder[i],i);
}
TreeNode root = builTree(inorder, postorder, 0, num-1, 0, num-1, inorderMap);
StringBuilder sbu = new StringBuilder();
preorder(root, sbu);
System.out.println("Preorder: "+sbu.toString().trim());
}
}
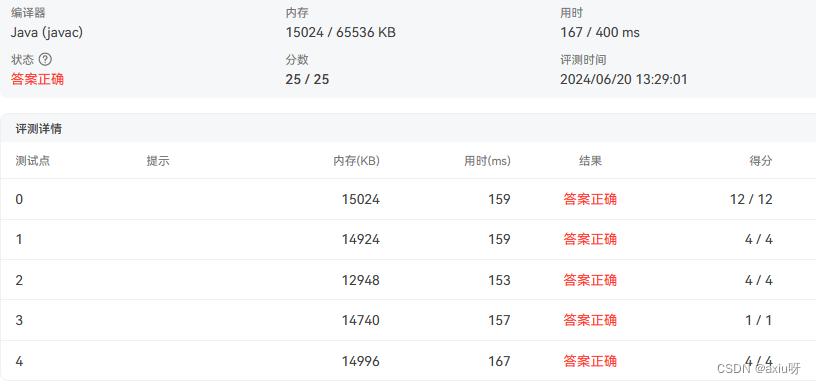
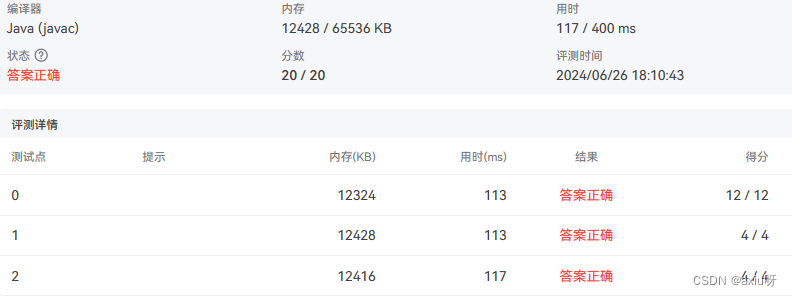
12-栈操作的合法性
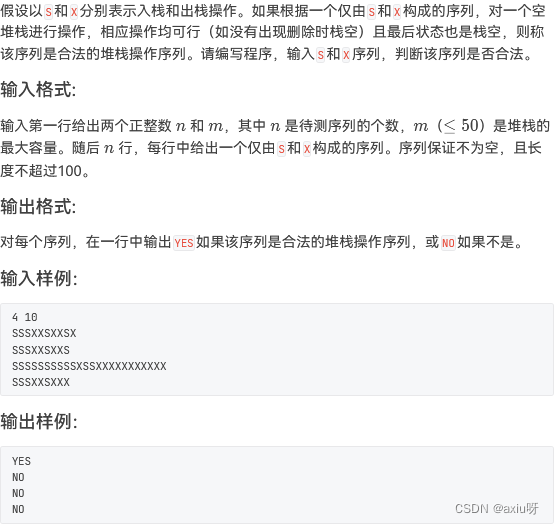
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
scanner.nextLine(); // 读取换行符
for (int i = 0; i < n; i++) {
String sequence = scanner.nextLine();
if (isValidSequence(sequence, m)) {
System.out.println("YES");
} else {
System.out.println("NO");
}
}
}
private static boolean isValidSequence(String sequence, int maxCapacity) {
int stackSize = 0;
for (char operation : sequence.toCharArray()) {
if (operation == 'S') {
stackSize++;
if (stackSize > maxCapacity) {
return false;
}
} else if (operation == 'X') {
stackSize--;
if (stackSize < 0) {
return false;
}
}
}
return stackSize == 0;
}
}
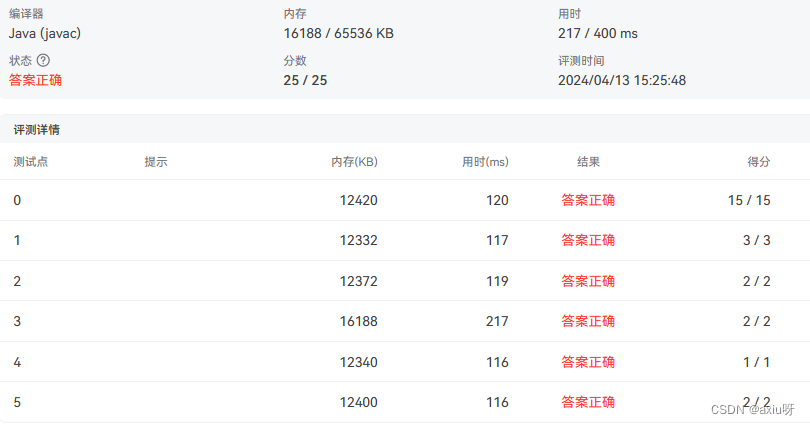
13-出栈序列的合法性
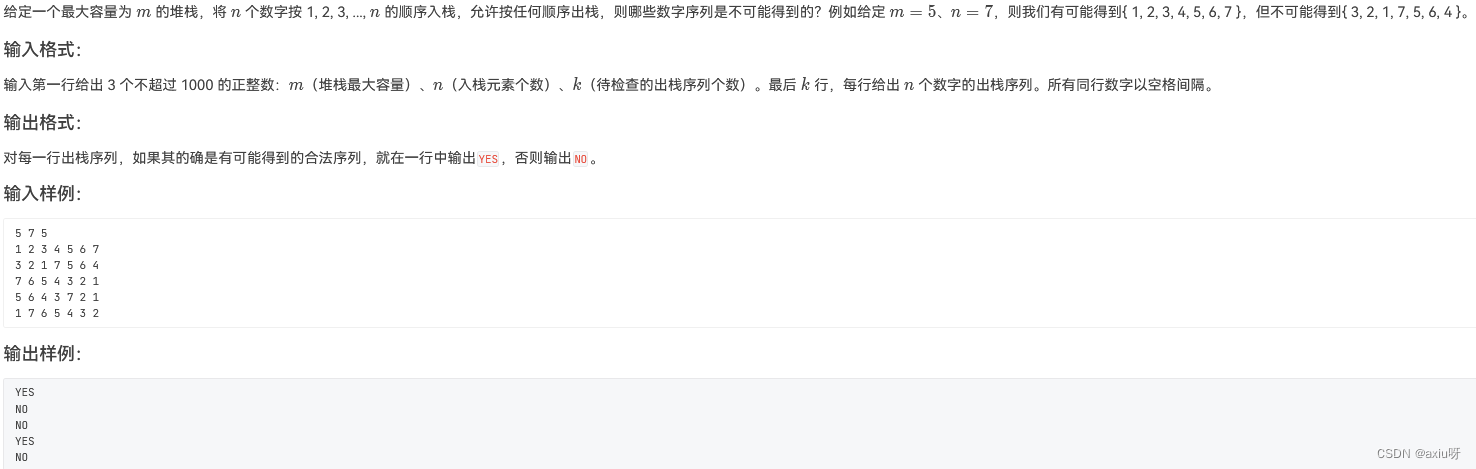
import java.util.Scanner;
import java.util.Stack;
public class Main {
private static boolean isValidSequence(int[] sequence, int m, int n) {
Stack<Integer> stack = new Stack<>();
int nextToPush = 1;
for (int i = 0; i < sequence.length; i++) {
int num = sequence[i];
// 确保所有小于等于当前num的自然数都已经入栈
while (nextToPush <= num) {
if (stack.size() == m) return false; // 检查是否栈溢出
stack.push(nextToPush++);
}
if (stack.peek() != num) return false; // 检查是否提前出栈
stack.pop();
}
return true;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int m = sc.nextInt(); // 栈容量
int n = sc.nextInt(); // 元素个数
int k = sc.nextInt(); // 测试序列数
String[] results = new String[k]; // 存储每个出栈序列的有效性结果
for (int i = 0; i < k; i++) {
int[] sequence = new int[n];
for (int j = 0; j < n; j++) {
sequence[j] = sc.nextInt(); // 读取每一个出栈序列
}
// 判断当前出栈序列是否有效，并将结果存入results数组
if (isValidSequence(sequence, m, n)) {
results[i] = "YES";
} else {
results[i] = "NO";
}
}
for (int i = 0; i < results.length; i++) {
String result = results[i];
System.out.println(result);
}
}
} 
14-完全二叉树的层序遍历
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
/*给定一棵完全二叉树的后序遍历，给出这棵树的层序遍历结果。
输入在第一行中给出正整数 N（≤30），即树中结点个数。
第二行给出后序遍历序列，为 N 个不超过 100 的正整数。同一行中所有数字都以空格分隔。*/
public class Main {
// 定义全局变量
static int num; //树的节点数量
// 定义一个静态数组 tree 存储完全二叉树的节点值，数组大小为 31 以适应最多 30 个节点的需求
static int[] BinaryTree = new int[31];
// 定义一个静态数组 arr，用于存放输入的节点值
static int[] data = new int[31];
// 定义一个静态队列 queue，存储树节点对应的下标，初始时添加所有可能的节点下标
static Queue<Integer> queue = new LinkedList<Integer>();
// 创建完全二叉树的递归
private static void createComplete(int i) {
// 节点下标大于总节点数时，结束递归
if (i > num) {
return;
}
createComplete(2*i); // 如果有左孩子，则编号为2i，
createComplete(2*i+1); // 如果有右孩子，编号为2i+1，
//然后按照后序遍历的方式（左右根），进行输入，最后顺序输出即可。
BinaryTree[i] = data[queue.remove()];
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
num = sc.nextInt();
// 初始化 queue，向其中添加从 1 到 30 的整数作为节点下标
for (int i = 1; i < 31; i++) {
queue.add(i);
}
for (int i = 0; i < num; i++) {
data[i+1] = sc.nextInt();
}
// 照层序遍历的方式生成完全二叉树
createComplete(1);
// 输出完全二叉树层序遍历的结果
for (int i = 1; i <= num; i++) {
// 输出第一个节点时不加空格，其余节点前面加上空格
if (i == 1) {
System.out.print(BinaryTree[i]);
} else {
System.out.print(" "+BinaryTree[i]);
}
}
}
}
