汉诺塔

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。 

---

n = 1

---

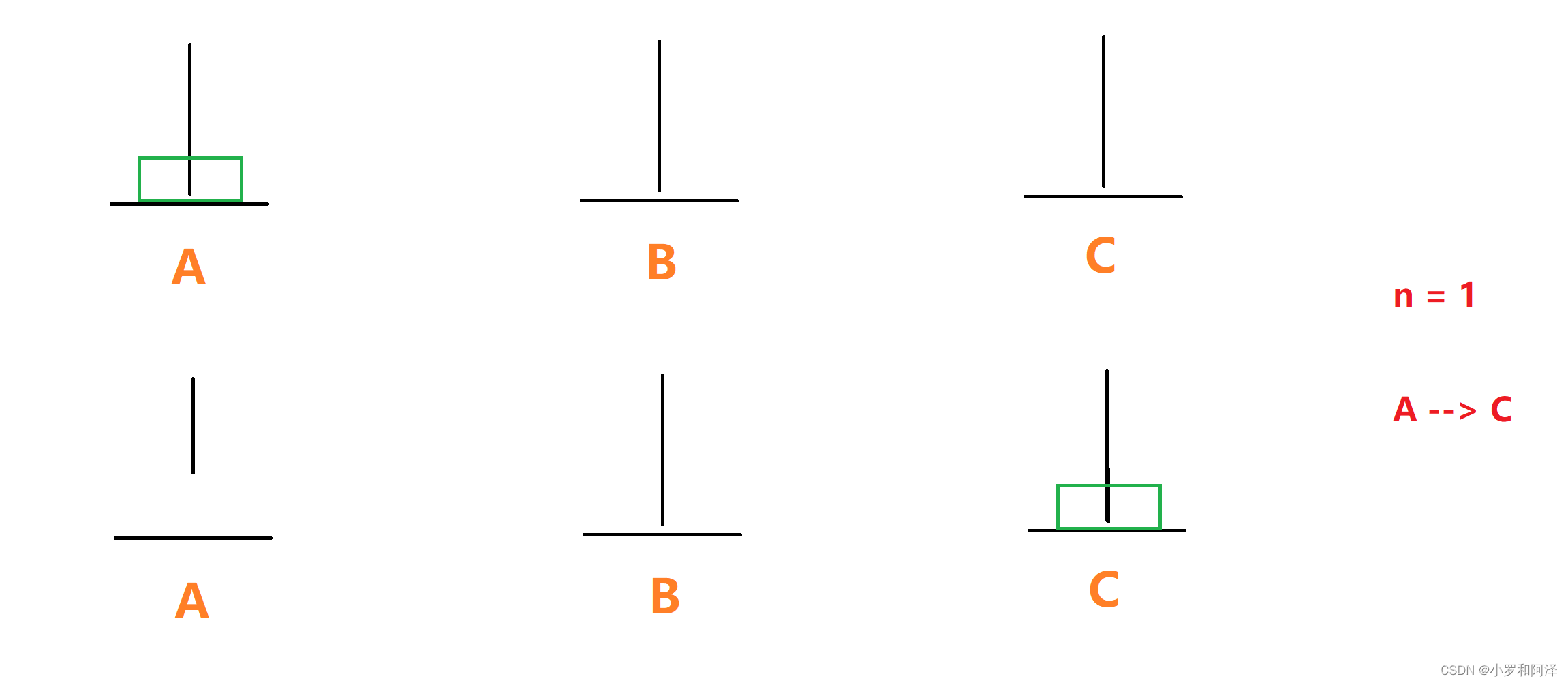
 n = 2

---

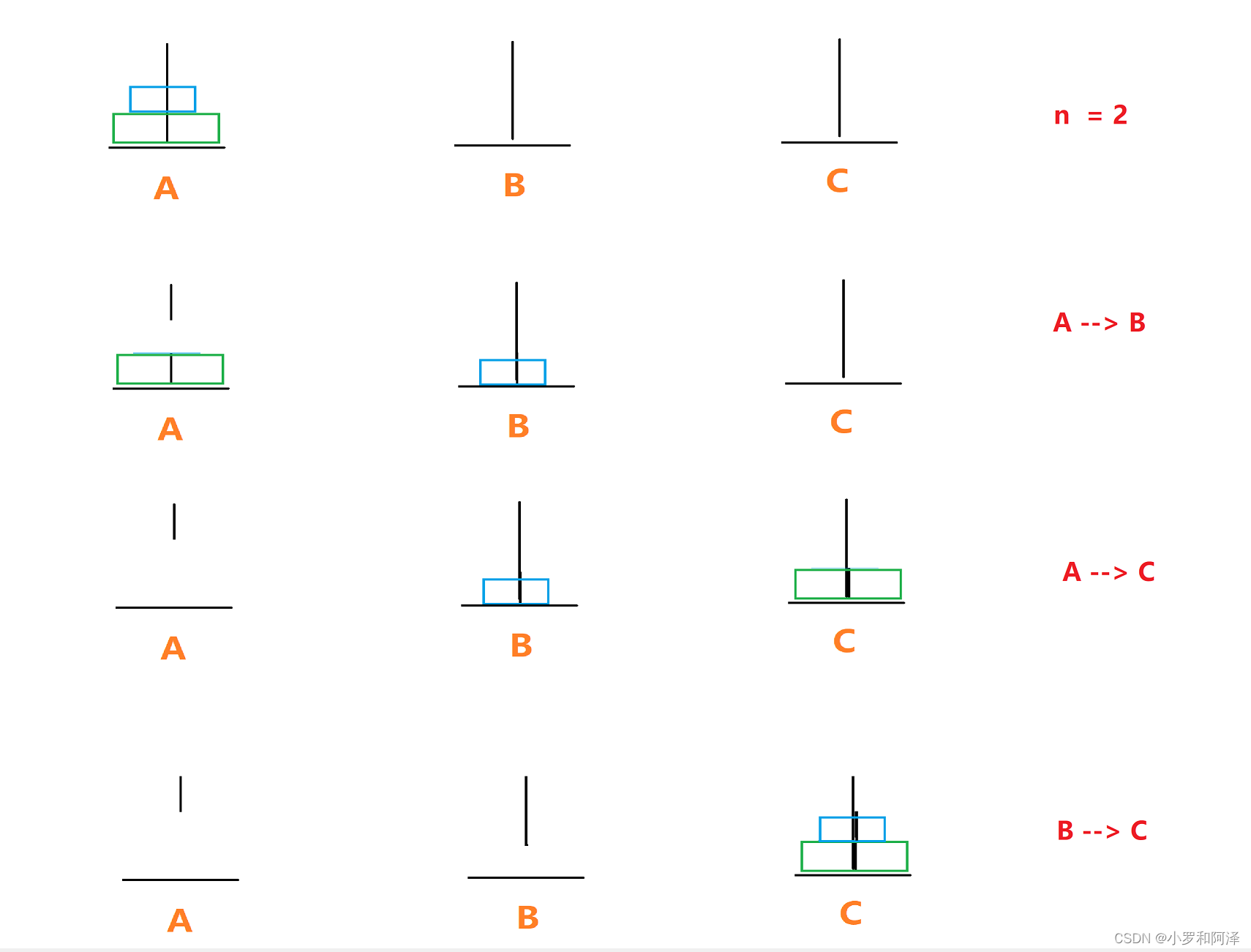
n = 3 

正常移动汉诺塔的步骤：

---

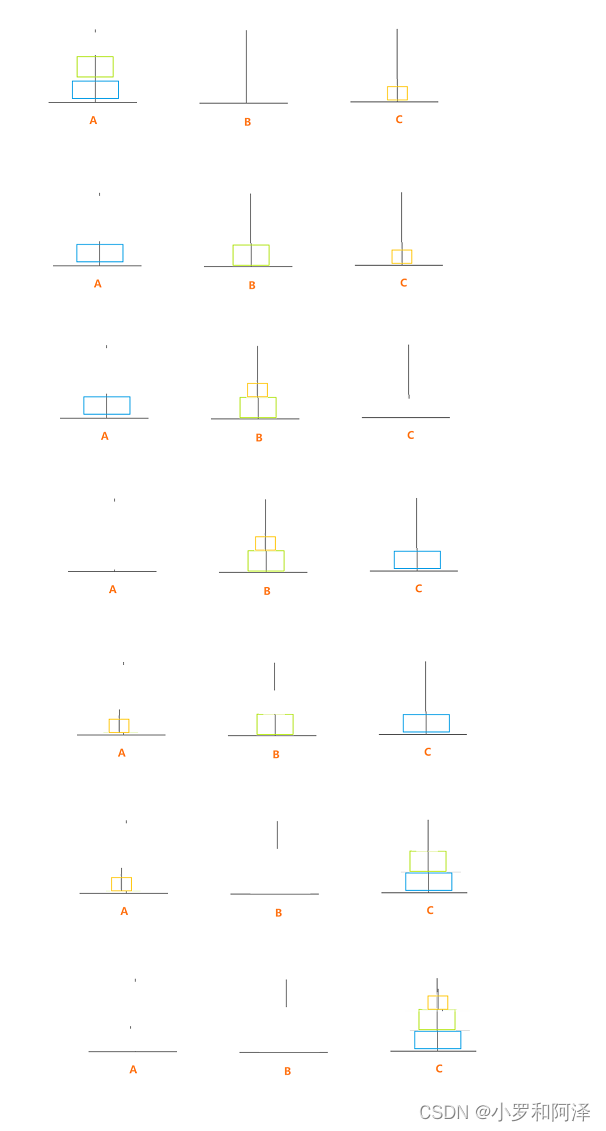
前面n = 1 和 n = 2 的时候 还比较简单，我们可以直接挪动。

下面我们用递归的思想再移动一下：

递归 就是 将复杂的问题简单化，详细的说就是 一个复杂的大问题 可以 化解成 多个相同的小问题，而这些小问题 可以 利用递归的思想逐一的解决。 

提前声明：

A ： 起始位置

B ： 中转位置

C ： 目标位置  

注意：此处的 起始位置 中转位置 目标位置 并不是固定的，具体的需要看我们怎么传参 

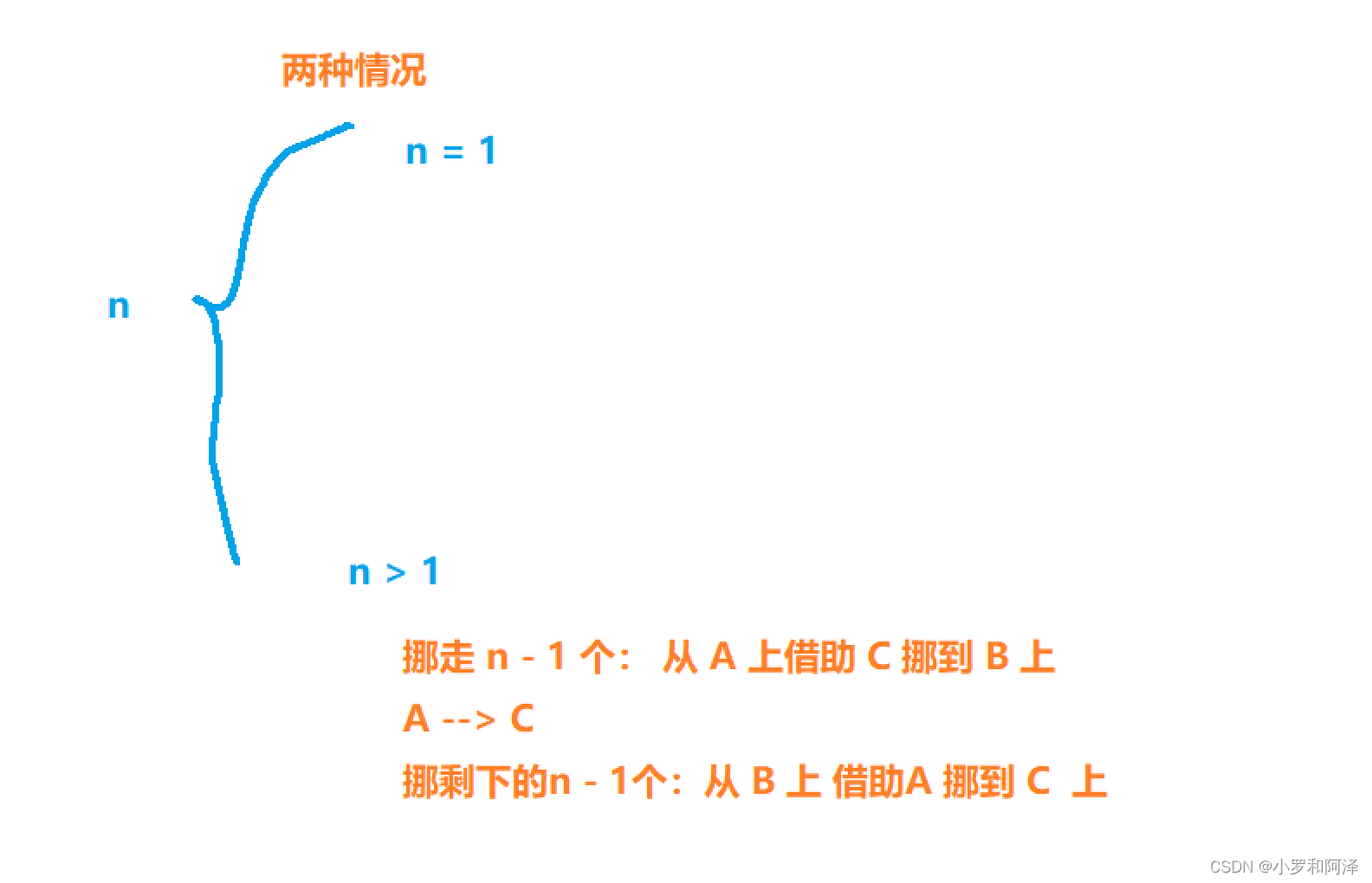
需要借助中转位置 去 帮助我们实现 将最下面 一层圆盘 移动到 目标位置 上 

     

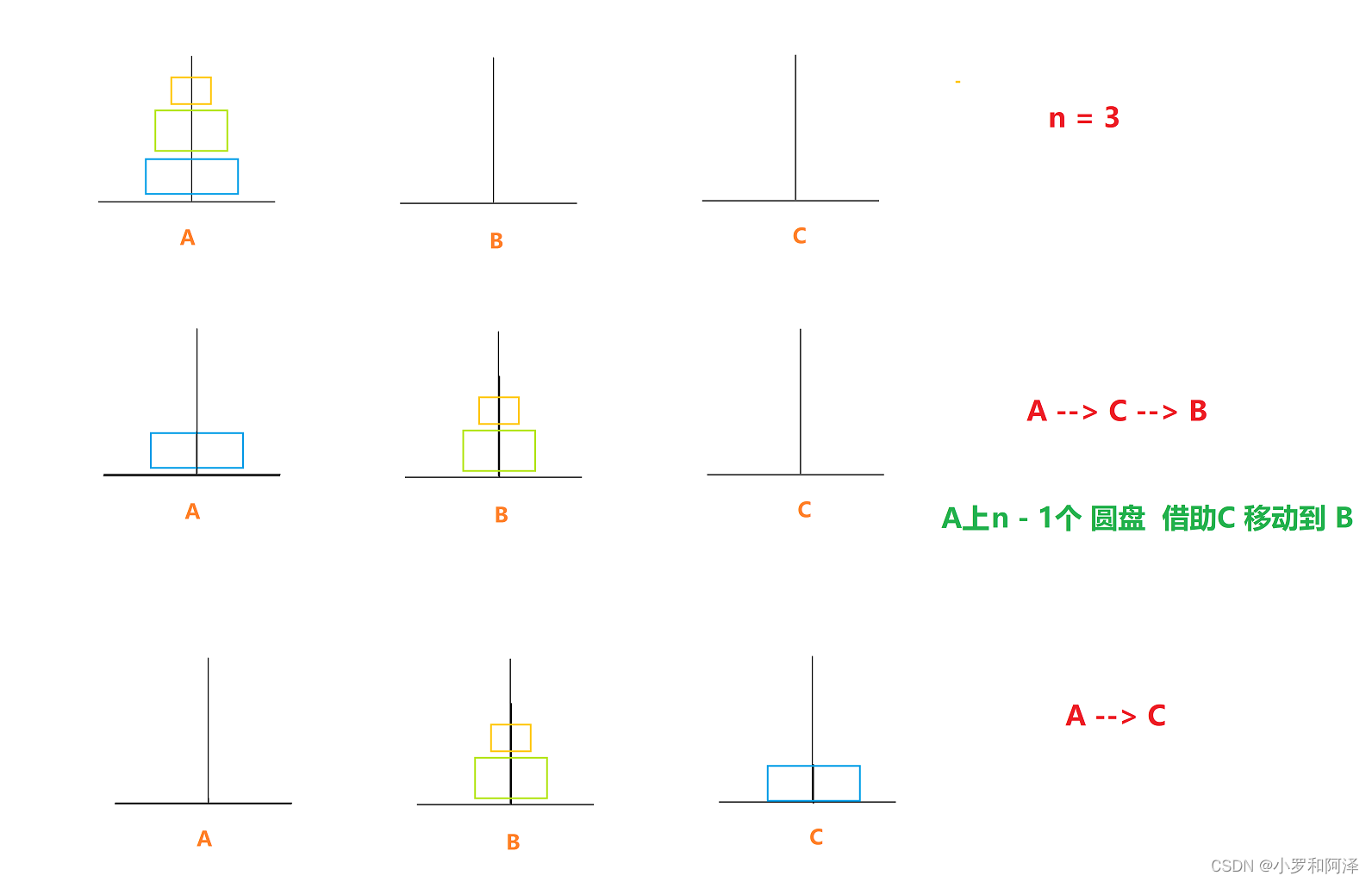
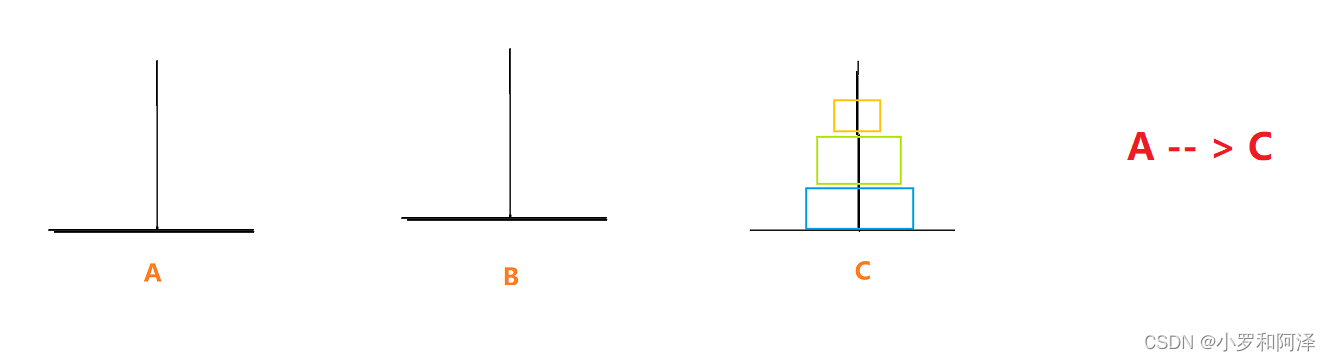
A 上 n - 1 个 圆盘 借助 C 移动到 B

解释： 此处 将n - 1 个 圆盘 移动到  中转位置 就需要递归的思想

我们 需要 把 n - 1 个圆盘 看作一个整体 直接 放到 B 上 （当然其中具体步骤还是比较麻烦的，但这些具体麻烦的步骤在递归中就已经实现了）

这时就体现我们递归的优点了，我们只需要关注 关键问题 其中比较繁琐的步骤 我们可以直接忽略 （文章结尾的代码 可以 清楚的看到） 

---

public static void move (char start, char end){
    System.out.print(start + " --> " + end + " ");
}

/**
 *
 * @param n 圆盘个数
 * @param pos1 起始位置
 * @param pos2 中转位置
 * @param pos3 目标位置
 */
public static void hanio (int n, char pos1 ,char pos2,char pos3){
    //结束递过程的条件
    if(n == 1){
        move(pos1,pos3);
    }else {
        hanio(n-1,pos1,pos3,pos2); //将 n-1 个圆盘 看成一个整体 借助 pos3 位置 移动到 pos2
        move(pos1,pos3);  //将最大最底层的 圆盘 放到 目标位置
        hanio(n-1,pos2,pos1,pos3); // 再将剩下的 n - 1 个 圆盘 从 pos2 借助 pos1 移动到 pos3
    }

}


public static void main(String[] args) {
    hanio(1,'A','B','C');
    System.out.println();
    hanio(2,'A','B','C');
    System.out.println();
    hanio(3,'A','B','C');
    System.out.println();
    hanio(4,'A','B','C');
}