Python面试宝典第4题：环形链表

news2024/10/6 4:06:11

题目

给你一个链表的头节点 head ，判断链表中是否有环。如果存在环，则返回 true 。否则，返回 false 。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

示例：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。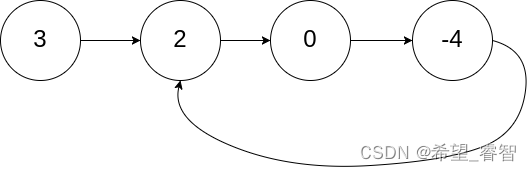

快慢指针法

快慢指针法，也叫Floyd判圈法，是解决链表中环检测问题的经典算法。其核心思想是使用两个指针，一个快指针每次移动两个节点，一个慢指针每次移动一个节点。如果链表中存在环，快慢指针最终会在环中的某一点相遇。若不存在环，快指针会先到达链表尾部。使用快慢指针法求解本题的主要步骤如下。

1、初始化指针。开始时，定义两个指针，一个快指针（fast）和一个慢指针（slow），均指向链表的头节点。

2、移动指针。每次迭代时，慢指针（slow）向前移动一步，快指针（fast）向前移动两步。如果链表中存在环，由于快指针移动速度是慢指针的两倍，最终快指针会追上慢指针。

3、终止条件。如果链表中没有环，快指针会首先到达链表的尾部（None），这时可以确定链表无环。相反，如果快慢指针相遇，则表明链表中存在环。

根据上面的算法步骤，我们可以得出下面的示例代码。

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

def create_linked_list(length, pos = -1):
    if length < 1 or (pos != -1 and (pos < 0 or pos >= length)):
        return None
    
    head = ListNode(0)
    current = head
    cycle_node = None
    
    for i in range(1, length + 1):
        new_node = ListNode(i)
        current.next = new_node
        current = new_node
        if i == pos + 1:
            cycle_node = new_node
    
    # 只有当pos有效且不为-1时，才创建环
    if cycle_node:
        current.next = cycle_node
    
    # 返回真正的头节点，忽略初始的0节点
    return head.next

def has_cycle_fast_slow_pointer(head):
    if head is None or head.next is None:
        return False
    
    slow = head
    fast = head.next
    
    while fast is not None and fast.next is not None:
        if slow == fast:
            return True
        slow = slow.next
        fast = fast.next.next
    
    return False

# 创建有环链表
head_with_cycle = create_linked_list(4, 1)
# 输出: True
print(has_cycle_fast_slow_pointer(head_with_cycle))

# 创建无环链表
head_no_cycle = create_linked_list(4, -1)
# 输出: False
print(has_cycle_fast_slow_pointer(head_no_cycle))

哈希表法

哈希表法利用数据结构中的哈希表来记录每个访问过的节点。由于哈希表的查找效率非常高，平均时间复杂度为O(1)，故我们可以在遍历链表的同时，将每个访问过的节点添加到哈希表中。当发现某个节点已经被访问过，即该节点存在于哈希表中时，则可断定链表中存在环。使用哈希表法求解本题的主要步骤如下。

1、初始化。创建一个空的哈希表，在Python中，通常是集合set。

2、遍历链表。从链表头开始遍历，对于每一个访问到的节点，执行以下操作。

（1）检查当前节点是否已经在哈希表中。

（2）如果不在，将当前节点添加到哈希表中，并继续遍历下一个节点。

（3）如果在哈希表中发现了当前节点，说明存在环，直接返回True。

3、遍历结束。如果遍历完整个链表都没有发现重复的节点，则说明链表中没有环，返回False。

根据上面的算法步骤，我们可以得出下面的示例代码。

def has_cycle_hashset(head):
    visited_nodes = set()
    while head is not None:
        # 如果节点已经在集合中，说明有环
        if head in visited_nodes:
            return True
        visited_nodes.add(head)
        head = head.next
    
    # 遍历结束，没有发现环
    return False

# 创建有环链表
head_with_cycle = create_linked_list(4, 1)
# 输出: True
print(has_cycle_hashset(head_with_cycle))

# 创建无环链表
head_no_cycle = create_linked_list(4, -1)
# 输出: False
print(has_cycle_hashset(head_no_cycle))