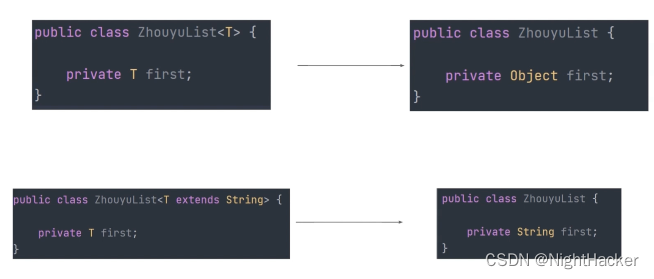
数据结构基本内容:1.时间复杂度 空间复杂度2.顺序表链表3.栈 队列4.二叉树5.排序
数据结构是存储,组织数据的方式.指相互之间存在一种或多种特定关系的数据元素的集合
算法是定义良好的计算过程.取一个或一组值为输入并产生一个或一组值为输出.
需要知道虽然选择题有20-30个代码题3-4个但是来开分差的都是代码题.
先理解再多加练习,数据结构差不多了去看看剑指学学思路.刷完这些内容之后坚持刷刷leetcode.
算法效率分为两种:一种是时间效率一种是空间效率.现在不怎么需要担心空间性,主要需要注意时间效率.
时间复杂度
时间复杂度:算法中基本操作的执行次数称为算法的事件复杂度.并不关系具体一个指令多少秒.

在这里 ++count 就是基本操作;两层循环嵌套,外层执行N次,内层也执行N次,所以基本操作有N ^ 2
所以认为它的时间复杂度是N ^ 2;
void Func1(int N){
int count = 0;
for (int i = 0; i < N; ++i){
for (int j = 0; j < N; ++j){
++count;
}
}
for (int k = 0; k < 2 * N; ++k){
++count;
}
int M = 10;
while (M--){
++count;
}
printf("%d\n",count);
}
Func1执行的基本操作次数:
F(N) = N^2 + 2*N + 10
N = 10 F(N) = 130
N = 100 F(N) = 10210
N = 1000 F(N) = 1002010
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而是只需要大概执行次数,那么我们使用大O的渐进表示法.
大O符号:适用于描述函数渐进行为的数学符号.
推导大O阶方法:
1.用常数1取代运行时间中的所有加法常数.
2.在修改后的运行次数函数中,只保留最高阶项
3.如果最高阶项存在且不是1,则去除与这个项目相乘的常数.得到的就是大O阶.
使用大O阶渐进表示法后,Func1的时间复杂度为:
O(N^2)
计算冒泡排序BubbleSort的时间复杂度
void BubbleSort(int* a, int n){
assert(a);
for (size_t end = n; end > 0;--end){
int exchange = 0;
for (size_t i = 1; i < end; ++i){
if (a[i - 1] > a[i]){
Swap(&a[i - 1],&a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
n - 1,n - 2,n - 3...0
最坏:F(n):n(n+1)/2 = 1/2 * n ^ 2 +1/2 * n
所以时间复杂度O(n ^ 2)
二分查找的时间复杂度O(lgn)
//计算阶乘递归Factorial时间复杂度
<表达式1>?<表达式2>:<表达式3> 在运算中,首第一个表达式进行检验,如果为真,则返回表达式2的值;如果为假,则返回表达式3的值。
long long Factorial(size_t N){
return N < 2 ? N : Factorial(N - 1) * N;
}
F(N)-->F(N-1)-->F(N-2)-->...-->1.需要N个递归调用,所以它的时间复杂度O(N).
//计算斐波那契递归Fibonacci的时间复杂度
long long Fibonacci(size_t N){
return N < 2 ? N : Fibonacci(N - 1) + Fibonacci(N - 2);
}
F(N)
F(N-1)F(N-2)
F(N-2)F(N-3)F(N-3)F(N-4)
......
F(1)
时间复杂度时O(2 ^ N).
空间复杂度
空间复杂度是一个算法在运行过程中临时占用存储空间大小的度量.空间复杂度不是程序占用了多少字节的空间,它计算的是变量的个数,基本和时间复杂度类似,也是用大O渐进法表示.
计算冒泡排序BubbleSort的时间复杂度
void BubbleSort(int* a, int n){
assert(a);
for (size_t end = n; end > 0;--end){
int exchange = 0;
for (size_t i = 1; i < end; ++i){
if (a[i - 1] > a[i]){
Swap(&a[i - 1],&a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
变量的个数5个是常数个所以空间复杂度是O(1).
//计算斐波那契递归Fibonacci的空间复杂度
long long* Fibonacci(size_t n){
if (n == 0)
return NULL;
long long* fibArray =
(long long*)malloc((n + 1)*sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i){
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}
变量n + 常数.所以空间复杂度是O(n).
//计算阶乘递归Factorial空间复杂度
long long Factorial(size_t N){
return N < 2 ? N : Factorial(N - 1) * N;
}
因为局部变量都是放在函数栈里,每调用一次函数会有一个函数栈,里面有一个变量N所以空间复杂度是O(n).
顺序表和链表
1.线性表2.顺序表3.链表4.顺序表和链表的区别和联系
线性表是n个具有相同特征的数据元素的有限序列.常见的线性表:顺序表 链表 栈 队列 数组...
线性表在逻辑上是线性的,也就是连续的一条直线,但它在物理结构上不一定是连续的,如果物理结构上连续是顺序表,如果物理上不连续就是链表.
顺序表是一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存储.在数组上完成数据的增删改查.
1.静态顺序表:使用定长数组存储
2.动态顺序表:使用动态开辟的数组存储
//顺序表的静态存储
#define N 10
typedef int SLDataType;
typedef struct SeqList{
SLDataType array[N]; //定长数组
size_t size; //有效数据的个数
}SeqList;
//顺序表的动态存储
typedef int SLDataType;
typedef struct seqList{
SLDataType*_data;//需要动态开辟的数组
size_t _size;//有效元素的个数
size_t _capacity;//当前可以存放的最大元素个数
}seqList;
静态数据表是开在栈上的,如果开太大会导致栈溢出
而动态数据表的大小只是一个指针加两个整数.
sizeof(静态):包含数组大小;sizeof(动态):不包含数组大小