时频分析思想萌芽于匈牙利物理学家 Gabor 在 1946 年所提出的 Gabor 展开理论,随后以此为基础发展出著名的线性时频变换方法—短时傅里叶变换。短时傅里叶变换假设分析信号在有限时长内具有平稳特性,它首先将时间与频率均为有限支撑的窗函数与分析信号进行内积,然后在固定窗长内计算傅里叶变换,并通过窗函数在时间方向上的不断平移,最终得到短时傅里叶变换的时频表示结果。值得注意的是,短时傅里叶变换的窗函数长度是固定不变的,窗函数的初始长度一旦确定,整个计算过程中的时频分辨率也就固定下来,因此合理选择窗函数的初始长度就显得尤为重要。此外,对于瞬时频率变化剧烈的强时变信号来说,由于窗函数长度与信号瞬时频率的变化情况无关,在窗函数移动过程中,被窗函数所截断的信号并不一定满足平稳信号的假设条件,因此短时傅里叶变换难以用于强时变信号的处理分析之中。为了解决窗函数长度固定不变所带来的弊端,
Morlet于1984 年引入小波概念,由此开启了信号的多分辨率分析时代。此外,Mallet在 1989 年搭建起小波的多分辨率理论框架,并实现了小波变换的快速算法。相对于短时傅里叶变换来说,小波变换较为明显的改进是其采用了可变尺度的窗函数。具体而言,由于信号低频分量变化缓慢、单个频率成分波动周期较长,因此小波变换利用较宽的窗函数分析信号的低频成分;与之相反,由于信号高频分量变化剧烈、单个频率成分波动周期较短,小波变换则采用较窄的窗函数对信号的高频成分进行处理。总之,小波变换将窗函数的长度与信号本身的频带分布直接关联起来,所以它能较好的处理分析信号各个频带下的时频特征。
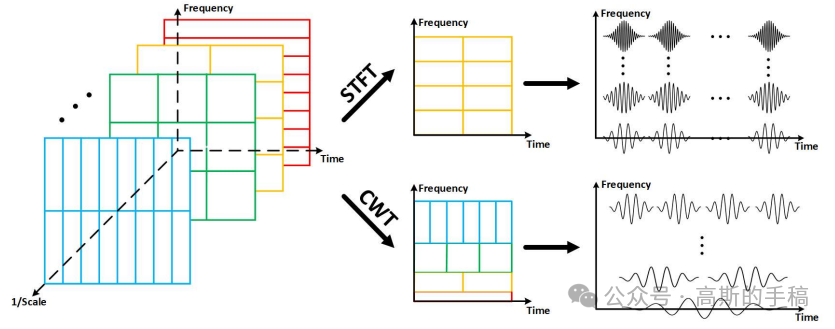
基函数在时频分析中的作用好比一把“刻度尺”,其中心频率数值类似于尺子上的刻度,信号与基函数的内积操作可看作信号在基函数上的投影度量过程,因此不论是短时傅里叶变换还是连续小波变换,时频表示结果均是由分布于整个时频平面上的基函数对分析信号进行度量得到的。考虑到基函数尺度的重要性,两种线性时频分析方法的基函数将在时间-频率-尺度三维空间中进行比较,其中尺度大小与基函数在时频平面上的表现密切相关。根据海森堡-加博尔不定原理的描述,对于选定函数形式的基函数来说,其时间宽度与频带宽度的乘积为一个常数,具体表现为基函数在时频平面上所占据的面积一定,所以较小尺度的基函数具有较小的时间宽度和较大的频带宽度,这意味着在度量分析信号时具有较高的时间分辨率和较差的频率分辨率,对于大尺度基函数而言,情况正好相反。
短时傅里叶变换的策略是根据经验选定一个较为合适的初始尺度,所有的基函数均分布于三维空间中的同一个尺度截面下,通过改变基函数的中心频率实现对分析信号的频率定位;小波变换的策略则是首先选择一个母小波基函数,然后通过拉伸或压缩操作实现母小波基函数尺度上的改变,因此小波变换的基函数分布于三维空间中不同的尺度截面,而基函数尺度的变化实现了对分析信号的频率定位。
由于没有考虑信号本身瞬时频率变化率的影响,小波变换事先在时频平面上为不同频段划定不同尺度基函数的做法不一定是合理的。
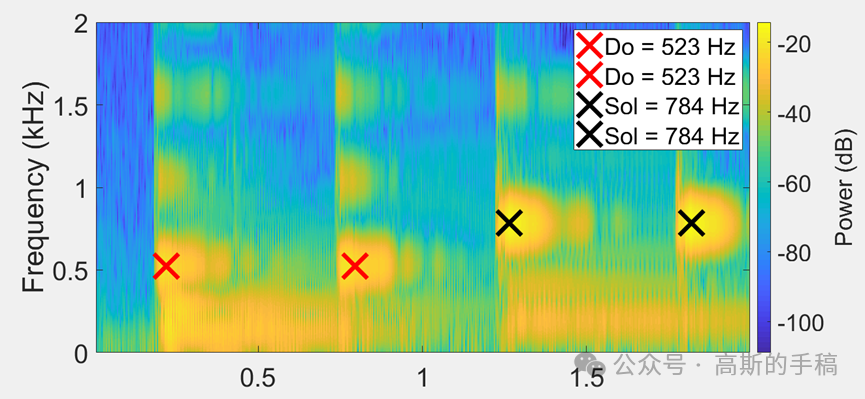
上图展示了一种构造信号的时频表示结果,其瞬时频率不断地增大而瞬时频率变化率却不断地减小,因此该构造信号低频成分需要较小尺度的基函数来分析,其高频成分则需要较大尺度的基函数来分析。对于小波变换来说,不论母小波基函数的尺度如何选择,均不能满足上述要求。为此,有学者提出一种衡量时频能量集中程度的指标,通过调整基函数尺度和 Chirprate 两个参数使得该指标在每个时频点处均达到最优,进而发展出最初的自适应线性时频变换方法,但其计算成本较大,不适合用于工程实践之中。
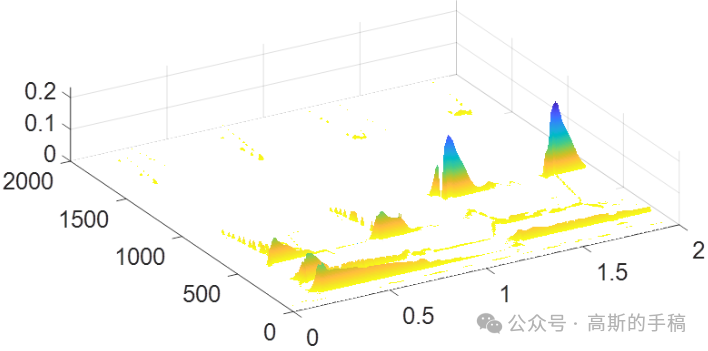
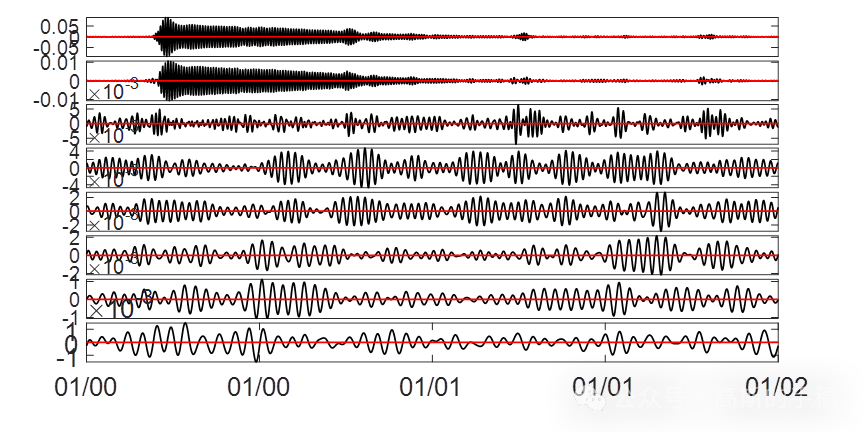
鉴于此,采用基于本征模态函数的方法对非平稳信号进行时频表示,运行环境为MATLAB 2018。
clear
close all
clc
[y,fs] = audioread('Little_star_by_Alice.mp4');
figure
plot(y(fs*21:fs*23))
sound(y(fs*21:fs*23),fs)
y=y(fs*21:fs*23);
%% Spectrogram
figure
tic
pspectrum(y,fs,'spectrogram','FrequencyLimits',[0,2000])
time_Spectrogram=toc;
title('')
hold on
plot3(0.7959,0.523,1,'xr','markersize',40,'linewidth',5)
plot3(0.22,0.523,1,'xr','markersize',40,'linewidth',5)
plot3(1.265,0.784,1,'xk','markersize',40,'linewidth',5)
plot3(1.82,0.784,1,'xk','markersize',40,'linewidth',5)
legend('Do = 523 Hz','Do = 523 Hz','Sol = 784 Hz','Sol = 784 Hz')
axis tight
set(gcf,'Units', 'Normalized', 'OuterPosition', [0 0 1 1]);
set(gca,'fontsize', 30);
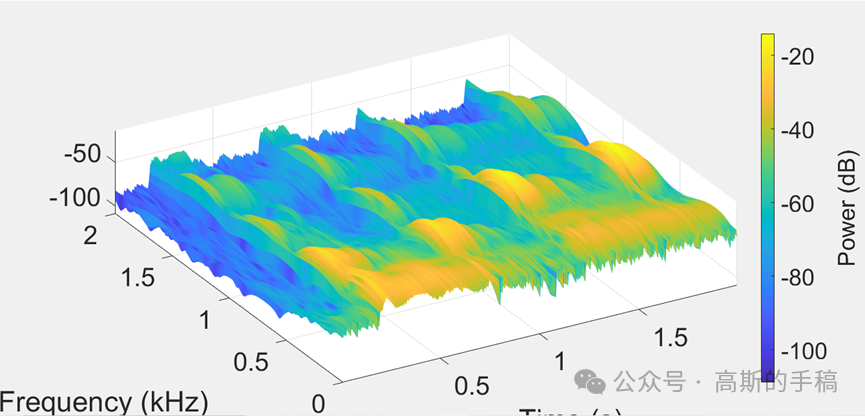
%% Spectrogram in 3D
figure
pspectrum(y,fs,'spectrogram','FrequencyLimits',[0,2000])
title('')
axis tight
view(330,67)
set(gcf,'Units', 'Normalized', 'OuterPosition', [0 0 1 1]);
set(gca,'fontsize', 30);
知乎学术咨询:
https://www.zhihu.com/consult/people/792359672131756032?isMe=1
工学博士,担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。


![【代码随想录】【算法训练营】【第56天】 [卡码98]所有可达路径](https://img-blog.csdnimg.cn/direct/a399aea782924ae4b00b0ce937c7afa4.png)