更多资料获取
📚 个人网站:ipengtao.com
大家好,今天为大家分享一个神奇的 Python 库 - iminuit。
Github地址:https://github.com/scikit-hep/iminuit
在科学计算和数据分析领域,参数估计和最优化是非常重要的任务。Python的iminuit库是一个基于MINUIT的Python封装,专门用于函数最小化和参数估计。MINUIT最初由CERN开发,广泛应用于高能物理实验中。iminuit库提供了高效、稳定的优化算法,适用于各种复杂的最优化问题。本文将详细介绍iminuit库,包括其安装方法、主要特性、基本和高级功能,以及实际应用场景,帮助全面了解并掌握该库的使用。
安装
要使用iminuit库,首先需要安装它。可以通过pip工具方便地进行安装。
以下是安装步骤:
pip install iminuit
安装完成后,可以通过导入iminuit库来验证是否安装成功:
import iminuit
print("iminuit库安装成功!")
特性
- 高效的最优化算法:基于MINUIT的高效算法,适用于复杂的参数估计问题。
- 简单易用的API:提供直观的API接口,方便用户快速上手。
- 自动微分:支持自动计算函数的梯度,简化了优化过程。
- 参数约束:支持对参数设置边界和固定值,灵活性强。
- 不确定性估计:提供参数的不确定性估计和误差传播功能。
基本功能
最小化简单函数
使用iminuit库,可以方便地最小化简单函数。
以下是一个示例:
import iminuit
# 定义待最小化的目标函数
def fcn(x, y):
return (x - 2)**2 + (y - 3)**2
# 创建Minuit对象并进行最小化
m = iminuit.Minuit(fcn, x=0, y=0)
m.migrad() # 运行最小化
# 输出结果
print(m.values) # 最优参数值
print(m.errors) # 参数误差
参数约束和固定
iminuit库支持对参数设置边界和固定值。
以下是一个示例:
import iminuit
# 定义待最小化的目标函数
def fcn(x, y):
return (x - 2)**2 + (y - 3)**2
# 创建Minuit对象,设置x参数的边界,并固定y参数
m = iminuit.Minuit(fcn, x=0, y=0)
m.limits["x"] = (1, 3) # 设置x参数的边界
m.fixed["y"] = True # 固定y参数
# 运行最小化
m.migrad()
# 输出结果
print(m.values)
print(m.errors)
不确定性估计
iminuit库提供了参数的不确定性估计功能。
以下是一个示例:
import iminuit
# 定义待最小化的目标函数
def fcn(x, y):
return (x - 2)**2 + (y - 3)**2
# 创建Minuit对象并进行最小化
m = iminuit.Minuit(fcn, x=0, y=0)
m.migrad()
# 计算参数的不确定性
m.hesse()
# 输出结果
print(m.values)
print(m.errors)
高级功能
自动微分
iminuit库支持自动计算目标函数的梯度,从而简化了优化过程。
以下是一个示例:
import iminuit
import numpy as np
# 定义待最小化的目标函数
def fcn(x, y):
return (x - 2)**2 + (y - 3)**2
# 使用NumPy的梯度计算功能
def grad(x, y):
df_dx = 2 * (x - 2)
df_dy = 2 * (y - 3)
return np.array([df_dx, df_dy])
# 创建Minuit对象,并传入梯度函数
m = iminuit.Minuit(fcn, x=0, y=0, grad=grad)
m.migrad()
# 输出结果
print(m.values)
print(m.errors)
参数扫描
iminuit库支持参数扫描,帮助用户分析目标函数在不同参数值下的行为。
以下是一个示例:
import iminuit
# 定义待最小化的目标函数
def fcn(x, y):
return (x - 2)**2 + (y - 3)**2
# 创建Minuit对象并进行最小化
m = iminuit.Minuit(fcn, x=0, y=0)
m.migrad()
# 扫描x参数的值,并记录目标函数值
scan = m.scan(n=10, x=(0, 4))
# 输出扫描结果
print(scan)
误差椭圆
iminuit库支持绘制参数的误差椭圆,帮助用户直观地理解参数之间的相关性。
以下是一个示例:
import iminuit
import matplotlib.pyplot as plt
# 定义待最小化的目标函数
def fcn(x, y):
return (x - 2)**2 + (y - 3)**2
# 创建Minuit对象并进行最小化
m = iminuit.Minuit(fcn, x=0, y=0)
m.migrad()
m.hesse()
# 绘制误差椭圆
fig, ax = plt.subplots()
m.draw_mncontour('x', 'y', numpoints=100, ax=ax)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Error Ellipse')
plt.show()
实际应用场景
实验数据拟合
在物理实验中,需要对实验数据进行拟合,以估计物理参数。
import numpy as np
import iminuit
import matplotlib.pyplot as plt
# 生成示例数据
x = np.linspace(0, 10, 100)
y = 3 * np.exp(-0.5 * x) + 0.1 * np.random.randn(100)
# 定义待拟合的模型函数
def model(x, a, b):
return a * np.exp(-b * x)
# 定义目标函数(最小化残差平方和)
def chi2(a, b):
return np.sum((y - model(x, a, b))**2)
# 创建Minuit对象并进行最小化
m = iminuit.Minuit(chi2, a=1, b=0.1)
m.migrad()
# 输出拟合结果
print(m.values)
print(m.errors)
# 绘制拟合结果
plt.scatter(x, y, label='Data')
plt.plot(x, model(x, *m.values), label='Fit', color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
参数估计与置信区间
在统计分析中,需要对参数进行估计,并计算其置信区间。
import numpy as np
import iminuit
# 生成示例数据
np.random.seed(42)
data = np.random.normal(loc=5, scale=2, size=100)
# 定义目标函数(负对数似然函数)
def neg_log_likelihood(mu, sigma):
return -np.sum(np.log(1/(sigma * np.sqrt(2 * np.pi)) * np.exp(-0.5 * ((data - mu) / sigma)**2)))
# 创建Minuit对象并进行最小化
m = iminuit.Minuit(neg_log_likelihood, mu=5, sigma=2)
m.migrad()
m.hesse()
# 输出参数估计结果
print(m.values)
print(m.errors)
# 计算参数的置信区间
ci_mu = m.mnprofile('mu', bound=(3, 7))
ci_sigma = m.mnprofile('sigma', bound=(1, 3))
print("mu的置信区间:", ci_mu)
print("sigma的置信区间:", ci_sigma)
优化问题求解
在工程优化问题中,需要最小化目标函数,以找到最佳设计参数。
import iminuit
# 定
义待最小化的目标函数
def objective(x, y):
return (x - 1)**2 + (y - 2)**2 + x*y
# 创建Minuit对象并进行最小化
m = iminuit.Minuit(objective, x=0, y=0)
m.migrad()
# 输出最优参数值
print(m.values)
print(m.errors)
# 扫描参数空间
scan = m.scan(n=10, x=(-1, 2), y=(0, 4))
print(scan)
总结
iminuit库是一个功能强大且易于使用的优化工具,能够帮助开发者高效地进行参数估计和最优化。通过支持高效的最优化算法、简单易用的API、自动微分、参数约束和不确定性估计,iminuit库能够满足各种复杂的最优化需求。本文详细介绍了iminuit库的安装方法、主要特性、基本和高级功能,以及实际应用场景。希望本文能帮助大家全面掌握iminuit库的使用,并在实际项目中发挥其优势。
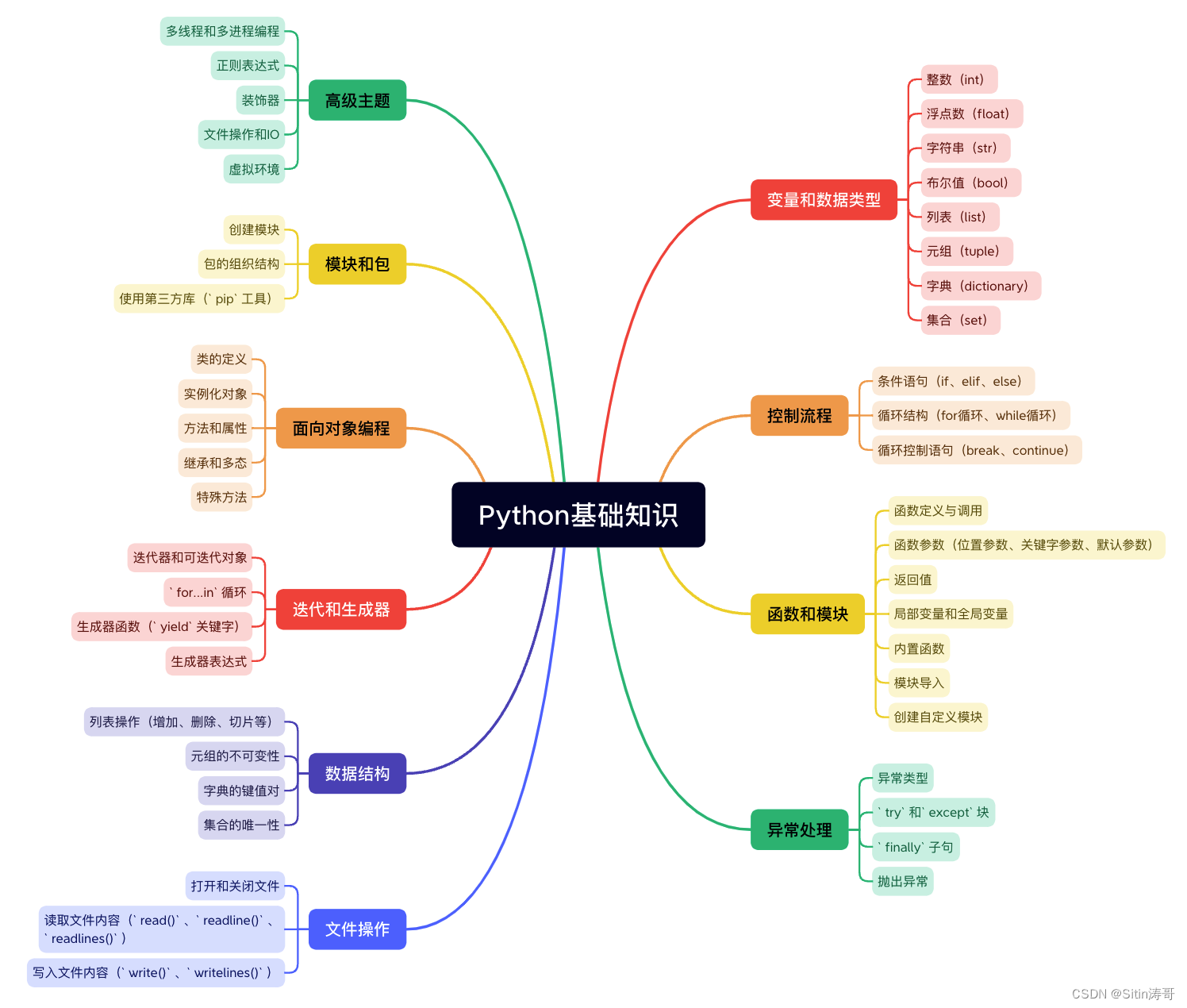
Python学习路线
更多资料获取
📚 个人网站:ipengtao.com
如果还想要领取更多更丰富的资料,可以点击文章下方名片,回复【优质资料】,即可获取 全方位学习资料包。

点击文章下方链接卡片,回复【优质资料】,可直接领取资料大礼包。

![[Information Sciences 2023]用于假新闻检测的相似性感知多模态提示学习](https://img-blog.csdnimg.cn/direct/0149dc1e13d84f81b8943b0fdd492d9c.png)