核心思想:因为队列都是一端进入另一端出(先进先出,后进后出),因此一个队列肯定是不能实现栈的功能的,这里就创建两个队列来模拟栈的先进后出,后进先出。 比如说如果是push操作我们肯定是要弹出栈顶元素(最后一个进栈的元素),而在队列中最后一个进队列的元素是在队尾,不可能实现第一个出(双端队列除外,这里我们不用双端队列)。因此我们应该有另外一个队列,我们把最后一个元素之前的所有元素都出队列,剩下那个元素就是模拟要出栈的那个元素。
1.Push操作
1.模拟进栈操作(实际上是队列)的时候看一下栈是否是空的,如果是空的那就把元素随便放进任意一个队列中,这里我们创建 qu1 和 qu2.我们就假设把元素放到qu1中,第一次进栈,随便进一个就好了。
2.如果qu1不为空,那么把元素加入到qu1中
3.如果qu2不为空,那么把元素加入到qu2中
上述操作就是入栈的效果,两个队列一个不断的进元素,另一个是辅助队列进行后续操作。
public void push(int x) {
if (empty()) {
qu1.offer(x);
return;
}
if (!qu1.isEmpty()) {
qu1.offer(x);
} else {
qu2.offer(x);
}
}2.Pop操作
1.如果栈是空的,不用弹出,只要返回-1就行了。
2.如果qu1不是空的,那么除了最后一个元素,就让qu1中的元素不断的出队列,直到只剩下一个元素。
3.与此同时,qu1中弹出去的元素不断的进入到qu2中。
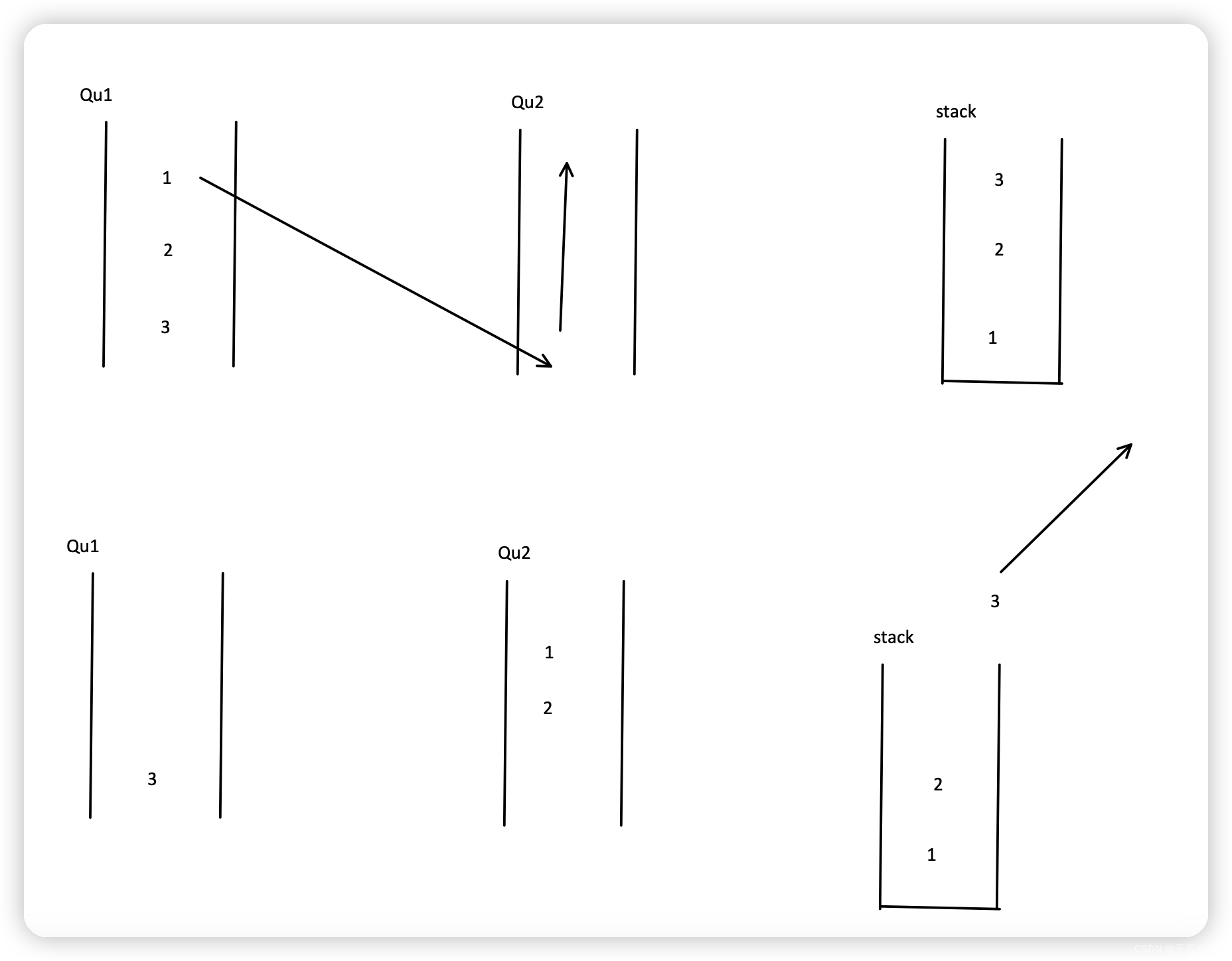
4.最后我们返回qu1中剩下的最后一个元素就行了。弹栈也就是弹最后一个入栈的元素。因此qu1中剩下的最后一个元素也就是我们想要的栈顶元素。
下面的图模拟了出栈的过程
public int pop() {
if (empty()) {
return -1;
}
// 找到不为空的队列 出size-1个元素
if (!qu1.isEmpty()) {
int size = qu1.size();
for (int i = 0; i < size - 1; i++) {
qu2.offer(qu1.poll());
}
return qu1.poll();
} else {
int size = qu2.size();
for (int i = 0; i < size - 1; i++) {
qu1.offer(qu2.poll());
}
return qu2.poll();
}
}3.Top操作:
这里top操作和pop操作多少有些类似,但是也不完全一样,我们用一个辅助的变量来返回栈顶元素。
1.还是栈为空就返回-1。
2.如果栈不为空,就让所有的元素都出队列,我们还是把qu1中的元素放到qu2中,当然也可以把qu2中的元素放到qu1中。
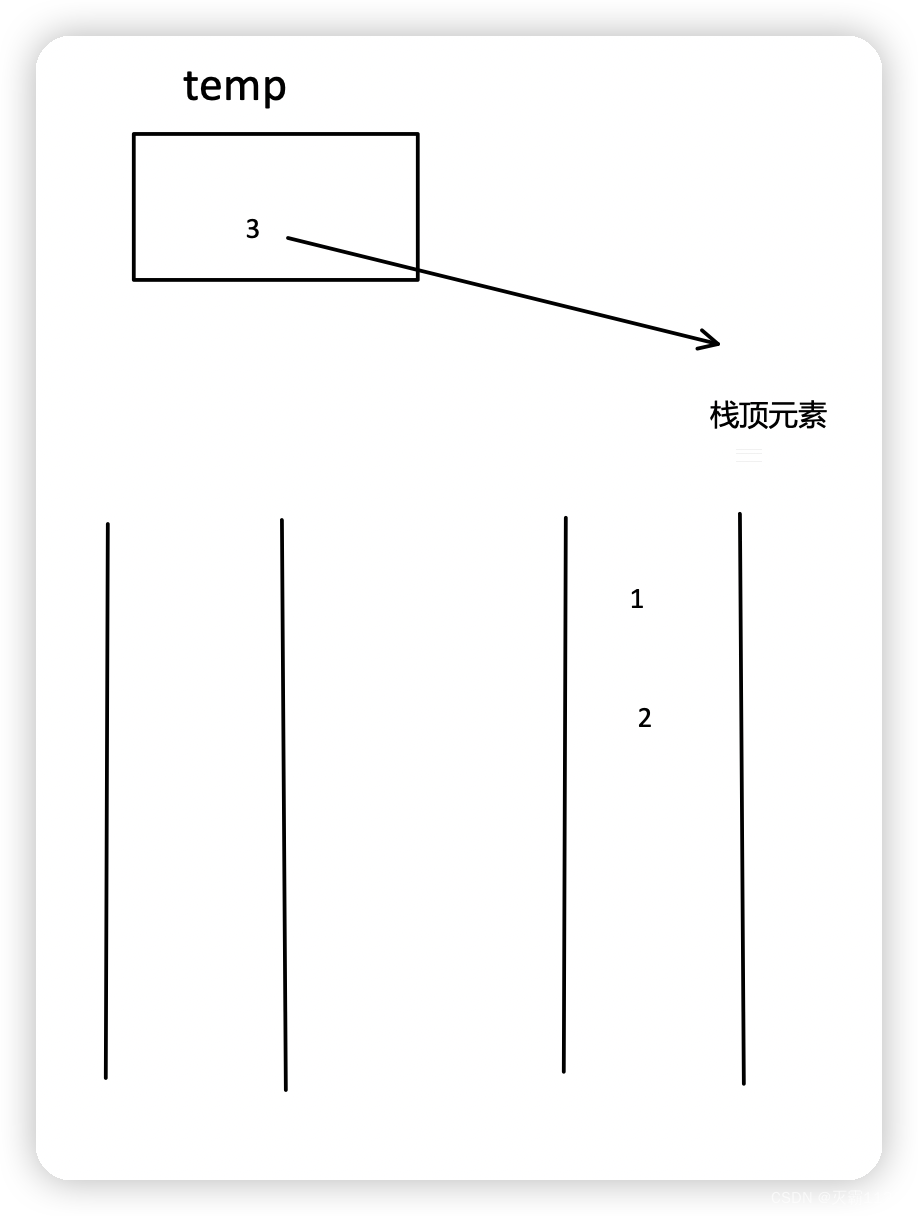
3.这回,所有的元素都要出队列,最后一个元素会保留在tmp中,因此我们只需要返回tmp即可。
下面三张图帮助理解这个过程


public int top() {
if (empty()) {
return -1;
}
if (!qu1.isEmpty()) {
int size = qu1.size();
int tmp = -1;
for (int i = 0; i < size; i++) {
tmp = qu1.poll();
qu2.offer(tmp);
}
return tmp;
} else {
int tmp = -1;
int size = qu2.size();
for (int i = 0; i < size; i++) {
tmp = qu2.poll();
qu1.offer(tmp);
}
return tmp;
}
}4.栈为空 empty操作
队列1和队列2 都为空,就是栈为空。
public boolean empty() {
return qu1.isEmpty() && qu2.isEmpty();
}5.全部的代码(Java)
class MyStack {
private Queue<Integer> qu1;
private Queue<Integer> qu2;
public MyStack() {
// 初始化两个队列
qu1 = new LinkedList<>();
qu2 = new LinkedList<>();
}
public void push(int x) {
// 如果栈为空,将元素添加到qu1中
if (empty()) {
qu1.offer(x);
return;
}
// 如果qu1不为空,将元素添加到qu1中
if (!qu1.isEmpty()) {
qu1.offer(x);
}
// 如果qu1为空,将元素添加到qu2中
else {
qu2.offer(x);
}
}
public int pop() {
// 如果栈为空,返回-1
if (empty()) {
return -1;
}
// 如果qu1不为空,将qu1中size-1个元素转移到qu2中,然后返回qu1中最后一个元素
if (!qu1.isEmpty()) {
int size = qu1.size();
for (int i = 0; i < size - 1; i++) {
qu2.offer(qu1.poll());
}
return qu1.poll();
}
// 如果qu1为空,将qu2中size-1个元素转移到qu1中,然后返回qu2中最后一个元素
else {
int size = qu2.size();
for (int i = 0; i < size - 1; i++) {
qu1.offer(qu2.poll());
}
return qu2.poll();
}
}
public int top() {
// 如果栈为空,返回-1
if (empty()) {
return -1;
}
// 如果qu1不为空,将qu1中的所有元素转移到qu2中,然后返回最后一个元素
if (!qu1.isEmpty()) {
int size = qu1.size();
int tmp = -1;
for (int i = 0; i < size; i++) {
tmp = qu1.poll();
qu2.offer(tmp);
}
return tmp;
}
// 如果qu1为空,将qu2中的所有元素转移到qu1中,然后返回最后一个元素
else {
int tmp = -1;
int size = qu2.size();
for (int i = 0; i < size; i++) {
tmp = qu2.poll();
qu1.offer(tmp);
}
return tmp;
}
}
public boolean empty() {
// 如果qu1和qu2都为空,返回true,表示栈为空
return qu1.isEmpty() && qu2.isEmpty();
}
}