快排的实现

news2024/10/5 19:13:57

引言

作为c语言库函数的一种，快排在排序中的地位毋庸置疑.

而更加具体的实现如图：

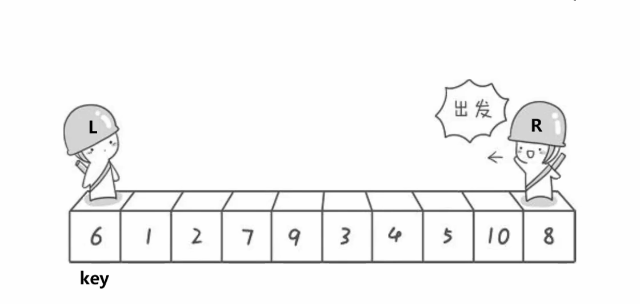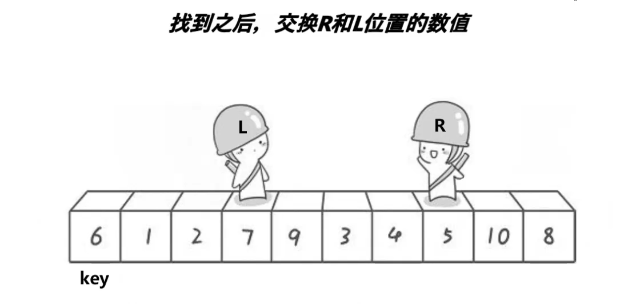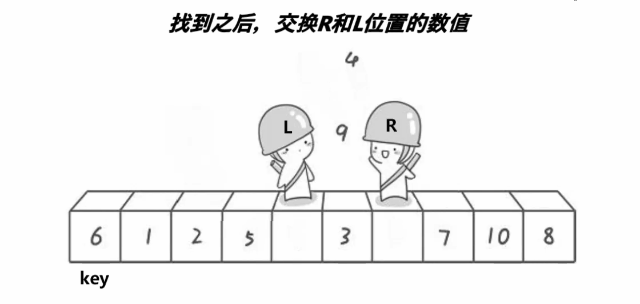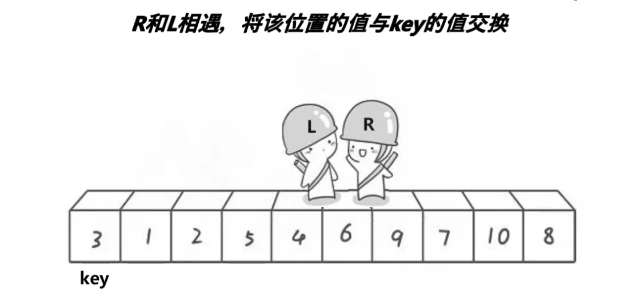
快排的实现（递归实现）

原理

单趟:先假定第一个数设为key,如果左边指针的值比key大，且右边指针的值比key小，则将其交换.当左右指针相遇，则左边都比key小，右边都比key大，则以中间为标识，中间位置一定比key小（后续证明）再对其左右进行排序（递归实现）

单趟排

代码实现如下：

void QuickSort(int* a, int left, int right)
{

	if (left >= right)
		return;

	int keyi = a[left];
	int begin = left, end = right;
	while (begin < end)
	{
		//右边找小
		while (begin < end && a[end] >= keyi)
		{
			--end;
		}
		//左边找大
		while (begin < end && a[end] <= keyi)
		{
			++begin;
		}
		Swap(&a[begin], &a[end]);
	}

	Swap(&keyi, &a[begin]);
	
}

多趟排

要想左右数组都有序，则通过递归实现将数组分割的效果，对分割再分割的数组进行排序，递归实现,代码如下：

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = a[left];
	int begin = left, end = right;
	while (begin < end)
	{
		//右边找小
		while (begin < end && a[end] >= keyi)
		{
			--end;
		}
		//左边找大
		while (begin < end && a[end] <= keyi)
		{
			++begin;
		}
		Swap(&a[begin], &a[end]);
	}

	Swap(&keyi, &a[begin]);
	keyi = begin;

	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi - 1, right);
}

但是这样的结构对于有序数组的排序有个致命的问题：栈溢出，这是由于keyi的取值固定为一边，keyi会被一直调整，所以我们期望取得一个中间值作为key.

避免有序情况下效率退化（key的取值）

一.三数取中

int GetMidi(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	// left midi right
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else // a[left] > a[midi]
	{
		if (a[midi] > a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

二.小区间优化

为了减少递归的次数，对于最后排到较小区间时，不再递归，而使用其他的排序结构，这里我们选择插入排序，因为它没有建二叉树，没有建堆，且排序速度较快.最后总代码如下：

int GetMidi(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	// left midi right
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else // a[left] > a[midi]
	{
		if (a[midi] > a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	// 小区间优化，不再递归分割排序，减少递归的次数
	if ((right - left + 1) < 10)
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		// 三数取中
		int midi = GetMidi(a, left, right);
		Swap(&a[left], &a[midi]);

		int keyi = left;
		int begin = left, end = right;
		while (begin < end)
		{
			// 右边找小
			while (begin < end && a[end] >= a[keyi])
			{
				--end;
			}

			// 左边找大
			while (begin < end && a[begin] <= a[keyi])
			{
				++begin;
			}

			Swap(&a[begin], &a[end]);
		}

		Swap(&a[keyi], &a[begin]);
		keyi = begin;
		// [left, keyi-1] keyi [keyi+1, right]
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
}