💓 博客主页：倔强的石头的CSDN主页 

           📝Gitee主页：倔强的石头的gitee主页

            ⏩ 文章专栏：《数据结构与算法》

                                  期待您的关注

 

​

 

目录

一、引言

堆排序的简介

堆排序的特点

二、堆的概念

三、堆排序算法的原理

四、堆排序的步骤

🍃构建堆 

🍃交换与调整

🍃重复过程

五、堆排序的性能分析

🍃时间复杂度：

🍃空间复杂度：

六、示例代码

七、总结

---

 

一、引言

堆排序的简介

堆排序（Heap Sort）是一种基于堆数据结构实现的排序算法。利用堆这种数据结构的高效性，通过构建和调整堆来实现排序，是一种性能优秀的排序算法。

堆排序的特点

1. 时间复杂度：堆排序的最坏、最好、平均时间复杂度均为O(nlogn)，其中n是待排序元素的数量。
2. 稳定性：堆排序在排序过程中相等的元素不会交换位置，因此它是稳定的排序算法。
3. 选择排序：堆排序是一种选择排序，它总是选择当前未排序部分的最大（或最小）元素进行排序。

 

二、堆的概念

关于堆的详细介绍，参考前置文章

【数据结构与算法】探索数组在堆数据结构中的妙用：从原理到实现-CSDN博客

 

三、堆排序算法的原理

• 堆排序的基本思想是将待排序的序列构建成一个堆，然后依次将堆顶元素与堆尾元素交换，并将堆的大小减小1，再对剩余的堆进行调整，使其满足堆的性质。
• 重复这个过程，直到堆的大小为1，此时排序完成。 

四、堆排序的步骤

🍃构建堆 

借助建堆算法，降序建小堆，升序建大堆，可以选择向上或者向下调整算法

向上调整建堆的原理：
模仿堆的插入操作来构建堆，从第一个子结点开始，将它看做是新插入的元素，向上调整至满足堆的性质，然后依次往后走，直到最后一个叶子节点完成上述调整

向下调整建堆的原理：
从最后一个父结点开始，先保证它和左右子树成为堆，然后依次往前走，保证每个父结点与左右子树成堆，直到最后根结点与左右子树成堆

 

关于建堆的向上调整算法和向下调整算法有时间复杂度推导

限于篇幅，这里就不展开推导了，直接给出结论

• 向下调整建堆的时间复杂度为O（N）
• 向上调整算法的时间复杂度为O（n*logN）

向下调整算法优于向上调整，所以应该选择向下调整算法

 这里分别给出向下调整建小堆和向下调整建大堆的算法

（如果关于向上调整算法和向下调整算法有疑惑，建议了解完堆的这篇文章之后再来看

【数据结构与算法】探索数组在堆数据结构中的妙用：从原理到实现-CSDN博客）

void Adjustdownsmall(DataType* a, int parent, int size)//向下调整建小堆算法
{
	
	int child = parent * 2 + 1;//先假定左孩子小
	while (child < size)//循环条件是未调整至叶子节点
	{
		if (child + 1 < size && a[child + 1] < a[child])//如果右孩子存在且更小，改变为右孩子
			child++;
		if (a[child] < a[parent])//如果子节点小于父节点，交换位置
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}
void Adjustdownbig(DataType* a, int parent, int size)//向下调整建大堆算法
{
	
	int child = parent * 2 + 1;//先假定左孩子大
	while (child < size)//循环条件是未调整至叶子节点
	{
		if (child + 1 < size && a[child + 1] > a[child])//如果右孩子存在且更大，改变为右孩子
			child++;
		if (a[child] > a[parent])//如果子节点大于父节点，交换位置
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}

 

🍃交换与调整

建堆之后，就是排序
以降序为例，每次将堆顶与堆尾数据交换（相当于将当前的最小值挪到最后），然后堆尾数据伪删除（有效数据个数--，不是真删除）进行一轮向下调整，恢复堆的结构

 

Swap(&a[0], &a[end]);//交换堆顶和堆尾数据
end--;
Adjustdownsmall(a, 0, end);//向下调整恢复堆的结构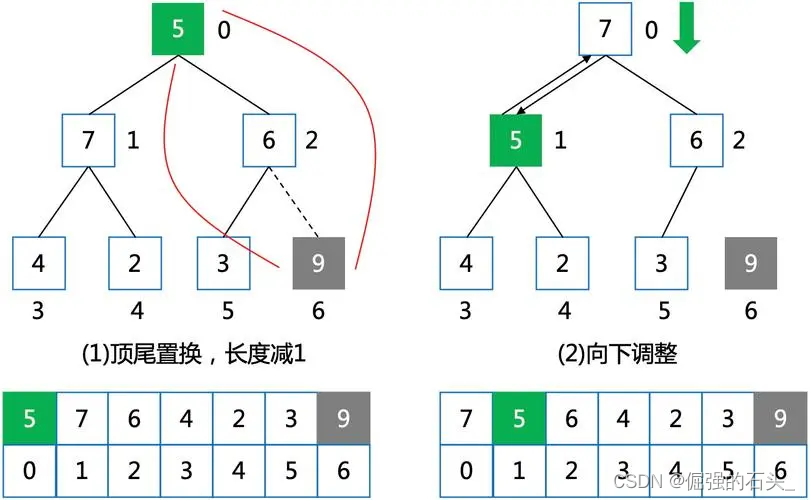

 

 

🍃重复过程

 重复上述交换与调整的过程，直到堆的大小为1，此时排序完成。

 

五、堆排序的性能分析

🍃时间复杂度：

1. 建堆：对于长度为n的数组，建堆的时间复杂度为O(n)。这是因为建堆的过程中，元素需要逐个从数组尾部加入到堆中，并重新调整堆的结构以维持其性质。每个元素加入堆中最多会触发从该元素到根节点的路径上元素的重新调整，因此，平均而言，每个元素会触发O(log n)次调整。所以，建堆的总时间复杂度为O(n *log n)。但是，由于建堆的过程是线性的（从最后一个非叶子节点开始，逐个向上调整），所以实际的时间复杂度为O(n)。
2. 排序：在排序阶段，每次从堆顶取出最大（或最小）元素，并重新调整堆结构的时间复杂度为O(log n)。因为需要排序n个元素，所以排序阶段的时间复杂度为O(n *log n)。

综上，堆排序的总时间复杂度为O(n) + O(n *log n) = O(n *log n)。

 

🍃空间复杂度：

堆排序的空间复杂度为O(1)。这是因为堆排序是原地排序算法，它只需要常数个额外的空间来存储临时变量，而不需要额外的存储空间来存储待排序的数组。所有的操作都是直接在原数组上进行的。所以，堆排序的空间复杂度非常低。

六、示例代码

（分别给出了完整的降序排序算法和升序排序算法）

#include<stdio.h>
#include<stdlib.h>

#if 1
//堆排序
typedef int DataType;
void Swap(DataType* a, DataType* b)
{
	DataType tmp = *a;
	*a = *b;
	*b = tmp;
}
void Adjustdownsmall(DataType* a, int parent, int size)//向下调整建小堆算法
{
	
	int child = parent * 2 + 1;//先假定左孩子小
	while (child < size)//循环条件是未调整至叶子节点
	{
		if (child + 1 < size && a[child + 1] < a[child])//如果右孩子存在且更小，改变为右孩子
			child++;
		if (a[child] < a[parent])//如果子节点小于父节点，交换位置
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}
void Adjustdownbig(DataType* a, int parent, int size)//向下调整建大堆算法
{
	
	int child = parent * 2 + 1;//先假定左孩子大
	while (child < size)//循环条件是未调整至叶子节点
	{
		if (child + 1 < size && a[child + 1] > a[child])//如果右孩子存在且更大，改变为右孩子
			child++;
		if (a[child] > a[parent])//如果子节点大于父节点，交换位置
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}

void HeapSortDOrder(DataType* a,int size)//降序排序
{
	
	//向下调整建小堆
	for (int i = (size - 2) / 2; i >= 0; i--)//从最后一个父节点调整
	{
		Adjustdownsmall(a, i, size);
	}
	int end = size - 1;
	while (end>0)
	{
		Swap(&a[0], &a[end]);//交换堆顶和堆尾数据
		end--;
		Adjustdownsmall(a, 0, end);//向下调整恢复堆的结构
	}
}
void HeapSortAOrder(DataType* a, int size)//升序排序
{

	//向下调整建大堆
	for (int i = (size - 2) / 2; i >= 0; i--)//从最后一个父节点调整
	{
		Adjustdownbig(a, i, size);
	}
	int end = size - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);//交换堆顶和堆尾数据
		end--;
		Adjustdownbig(a, 0, end);//向下调整恢复堆的结构
	}
}
#endif

void print(DataType* a, int size)
{
	for (int i = 0; i < size; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}
int main()
{
	int arr[] = { 12,3,5,78,46,15,23,19,20,36,52 };
	int size = sizeof(arr) / sizeof(arr[0]);
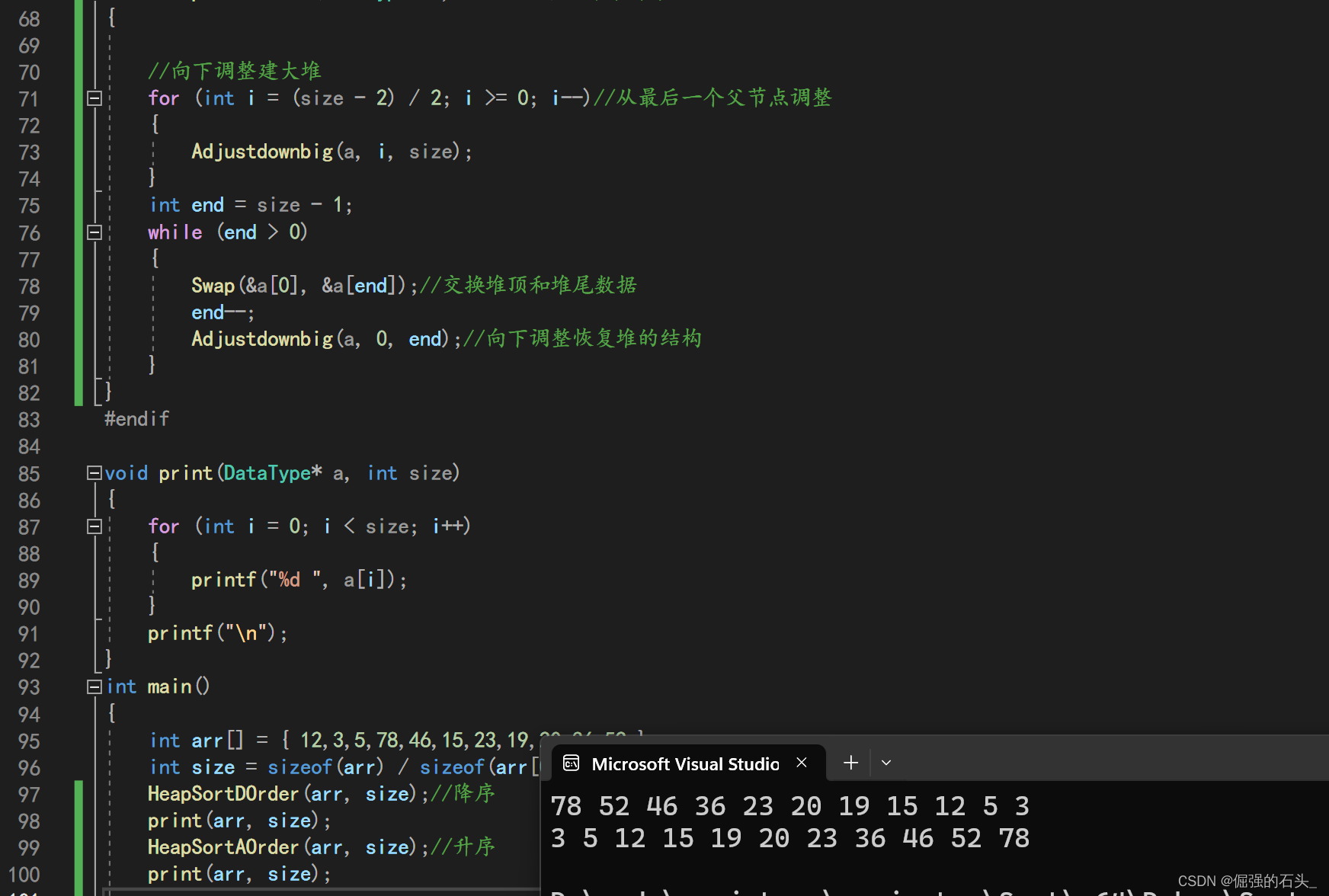
	HeapSortDOrder(arr, size);//降序
	print(arr, size);
	HeapSortAOrder(arr, size);//升序
	print(arr, size);

}

 

七、总结

堆排序算法是一种高效且实用的排序算法，它通过利用堆数据结构的特点和性质，实现了对数据的高效排序。在实际应用中，我们可以根据问题的特点选择使用堆排序算法，以提高程序的性能和效率。