【Python实战因果推断】13_线性回归的不合理效果3

news2024/11/17 13:26:10

Regression Theory

Single Variable Linear Regression

Multivariate Linear Regression

Frisch-Waugh-Lovell Theorem and Orthogonalization

Regression Theory

我不打算太深入地探讨线性回归是如何构建和估计的。不过，一点点理论知识将有助于解释线性回归在因果推理中的作用。首先，回归解决的是最佳线性预测问题。假设 β* 是一个参数向量：

$\beta^\star=argmin E\Big[(Y_i-X_i'\beta)^2\Big]$

线性回归可以找到最小化均方误差 (MSE) 的参数。如果将其微分并设为零，就会发现这个问题的线性解如下：

$\beta^\star=E[X'X]^{-1}E[X'Y]$

也可以用样本估计beta

$\hat{\beta}=(X'X)^{-1}X'Y$

但不要相信我的话。如果你是那种理解代码胜过理解公式的人，那就自己试试吧。在下面的代码中，我使用 OLS 的代数解来估计你刚才看到的模型的参数（我添加了截距作为最终变量，因此第一个参数估计值将是 β1）：

 X_cols = ["credit_limit", "wage", "credit_score1", "credit_score2"]
 X = risk_data[X_cols].assign(intercep=1)
 y = risk_data["default"]
 def regress(y, X):
 return np.linalg.inv(X.T.dot(X)).dot(X.T.dot(y))
 beta = regress(y, X)
 beta
 
 array([ 3.062e-06, -8.821e-05, -4.174e-05, -3.039e-04, 4.0364-01])

如果你回过头来看一下，就会发现这些数字与你之前用 statsmodels 中的 ols 函数估计模型时得到的数字完全相同。

Single Variable Linear Regression

上一节的 β 公式非常通用。不过，研究一下只有一个回归变量的情况还是有好处的。在因果推断中，您经常想要估计一个变量 T 对结果 y 的因果影响，因此，您使用这个单一变量的回归来估计这种影响。

在只有一个回归变量 T 的情况下，与之相关的参数为

$\hat{\tau}=\frac{Cov\big(Y_i,T_i\big)}{Var\big(T_i\big)}=\frac{E\big[\big(T_i-\overline{T}\big)\big(Y_i-\overline{Y}\big)\big]}{E\big[\big(T_i-\overline{T}\big)^2\big]}$

如果 T 是随机分配的，β1 就是 ATE。重要的是，通过这个简单的公式，您可以了解回归的作用。它是要找出干预和结果是如何共同作用的（用分子中的协方差表示），然后用干预的单位来表示，即除以干预的方差。

Multivariate Linear Regression

原来，除了你之前看到的一般公式之外，还有另一种方法来看待多元线性回归。这另一种方法让我们对回归的作用有了一些了解。

如果你有不止一个回归变量，你可以扩展单变量回归公式以适应这种情况。假设其他变量只是辅助变量，而您真正感兴趣的是估计与 T 相关的参数 τ：

$y_{i}=\beta_{0}+\tau T_{i}+\beta_{1}X_{1i}+ . . . +\beta_{k}X_{ki}+u_{i}$

$\tau$ 可以用以下公式来估计： $\hat{\tau}=\frac{Co\nu\left(Y_i,\widetilde{T_i}\right)}{Var\left(\widetilde{T_i}\right)}$ , 其中 $\widetilde{T}_i$ 是Ti对所有其他协变量 $X_{1i}+ . . . +X_{ki}$ 回归的残差。

现在，让我们来体会一下这有多酷。这意味着多元回归的系数是同一回归变量在考虑了模型中其他变量的影响后的二元系数。用因果推理的术语来说， $\tau$ 是使用所有其他变量预测 T 后的双变量系数。

这背后有一个很好的直觉。如果能用其他变量预测 T，就意味着它不是随机的。然而，一旦控制了所有干扰变量 X，你就可以让 T 看起来和随机的一样好。为此，你可以使用线性回归从混杂因子中预测它，然后取该回归 $\widetilde{T}$ 的残差。根据定义， $\widetilde{T}$ 不能被你已经用来预测T的其他变量X来预测。相当优雅地说， $\widetilde{T}$ 是与 X 中任何其他变量都不相关（不相关）的干预版本。

我知道这很拗口，但实在是太神奇了。事实上，这已经是我答应要教大家的 FWL 定理的工作原理了。所以，如果你还不太理解多元回归部分，也不用担心，因为接下来你将以一种更直观、更形象的方式来复习它。

Frisch-Waugh-Lovell Theorem and Orthogonalization

FWL 式正交化是您可以使用的第一种主要去杂技术。它是一种简单而强大的方法，可以让非实验数据看起来像是经过随机干预的。FWL 主要是关于线性回归的；FWL 式正交化已经扩展到了更广泛的环境中，你将在第三部分中看到。Frisch-Waugh-Lovell 定理指出，多元线性回归模型可以一次性或分三步进行估计。例如，您可以将违约与信贷限额、工资、信贷评分 1 和信贷评分 2 进行回归，就像您已经做的那样：

 formula = 'default ~ credit_limit + wage+credit_score1+credit_score2'
 model = smf.ols(formula, data=risk_data).fit()
 model.summary().tables[1]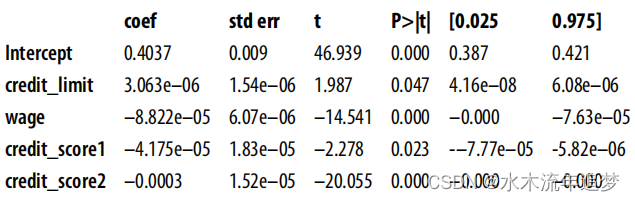

但是，根据 FWL，您还可以将这一估算细分为
1. 去偏步骤，将干预 T 与混杂因素 X 进行回归，得到干预残差 $\tilde{T}=T-\hat{T}$
2. 去噪步骤：将结果 Y 与混杂变量 X 进行回归，得到结果残差 Y。
3. 结果模型，将结果残差 Y 与干预残差 T 进行回归，得到结果残差 Y = Y - Y 3.
残差 T，得到 T 对 Y 的因果效应的估计值。