Pytorch实战（二）

文章目录

前言
一、LeNet5原理
- 1.1LeNet5网络结构
- 1.2LeNet网络参数
- 1.3LeNet5网络总结
二、AlexNext
- 2.1AlexNet网络结构
- 2.2AlexNet网络参数
- 2.3Dropout操作
- 2.4PCA图像增强
- 2.5LRN正则化
- 2.6AlexNet总结
三、LeNet实战
- 3.1LeNet5模型搭建
- 3.2可视化数据
- 3.3加载训练、验证数据集
- 3.4模型训练
- 3.5可视化训练结果
- 3.6模型测试
四、AlexNet实战

前言

参考原视频：哔哩哔哩。

一、LeNet5原理

1.1LeNet5网络结构

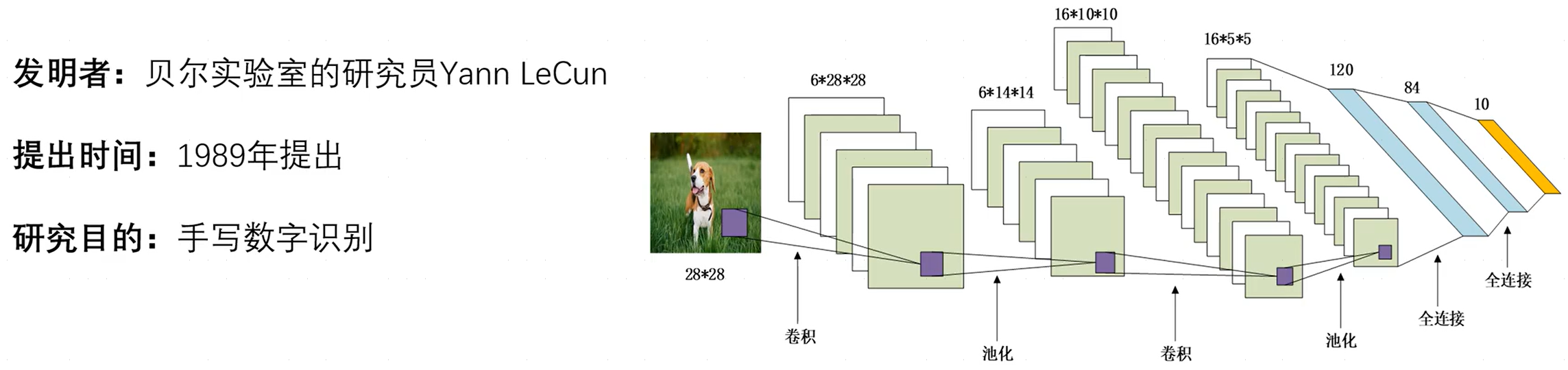
在这里插入图片描述
LeNet-5，其中， $5$ 表示神经网络中带有参数的网络层数量为 $5$ ，如卷积层带有参数 $(w, b)$ ，而池化层仅仅是一种操作，并不带有参数，而在LeNet-5中共含有两层卷积层、三层全连接层（有一层未标出）。
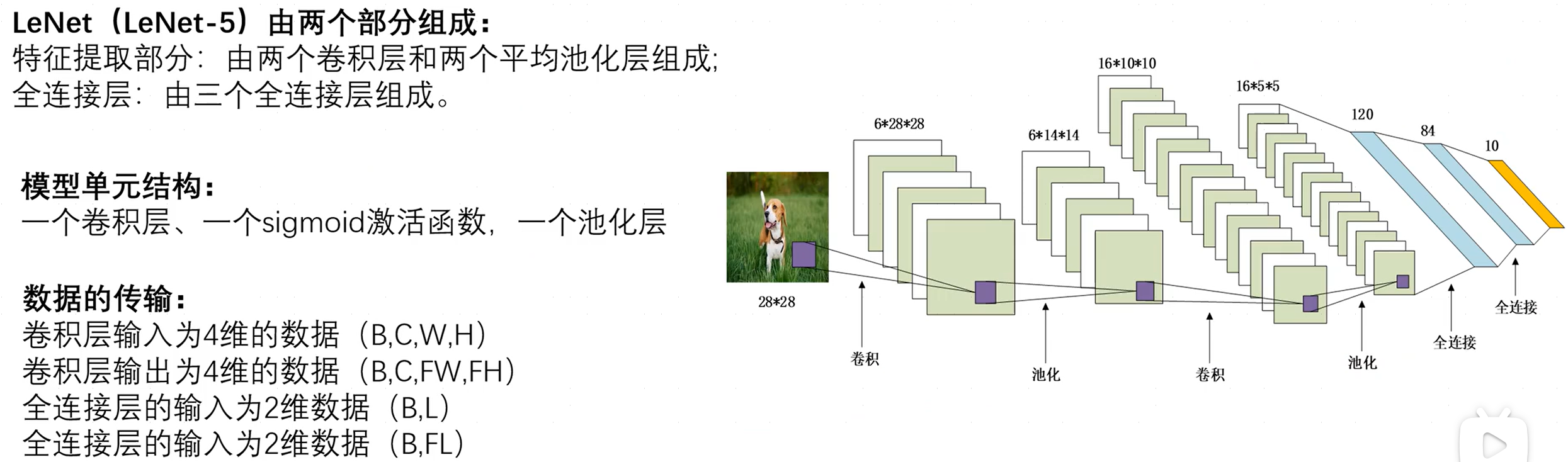
在这里插入图片描述

卷积层和池化层：用于提取特征。
全连接层：一般位于整个卷积神经网络的最后，负责将卷积输出的二维特征图转化成一维的一个向量（将特征空间映射到标记空间），由此实现了端到端的学习过程（即：输入一张图像或一段语音，输出一个向量或信息）。全连接层的每一个结点都与上一层的所有结点相连因而称之为全连接层。由于其全相连的特性，一般全连接层的参数也是最多的。

事实上，不同的卷积核提取的特征并不相同，比如猫、狗、鸟都有眼睛，而如果只用局部特征的话不足以确定具体类别，此时就需要使用全连接层组合这些特征来最终确定是哪一个分类，即起到组合特征和分类器功能。

1.2LeNet网络参数

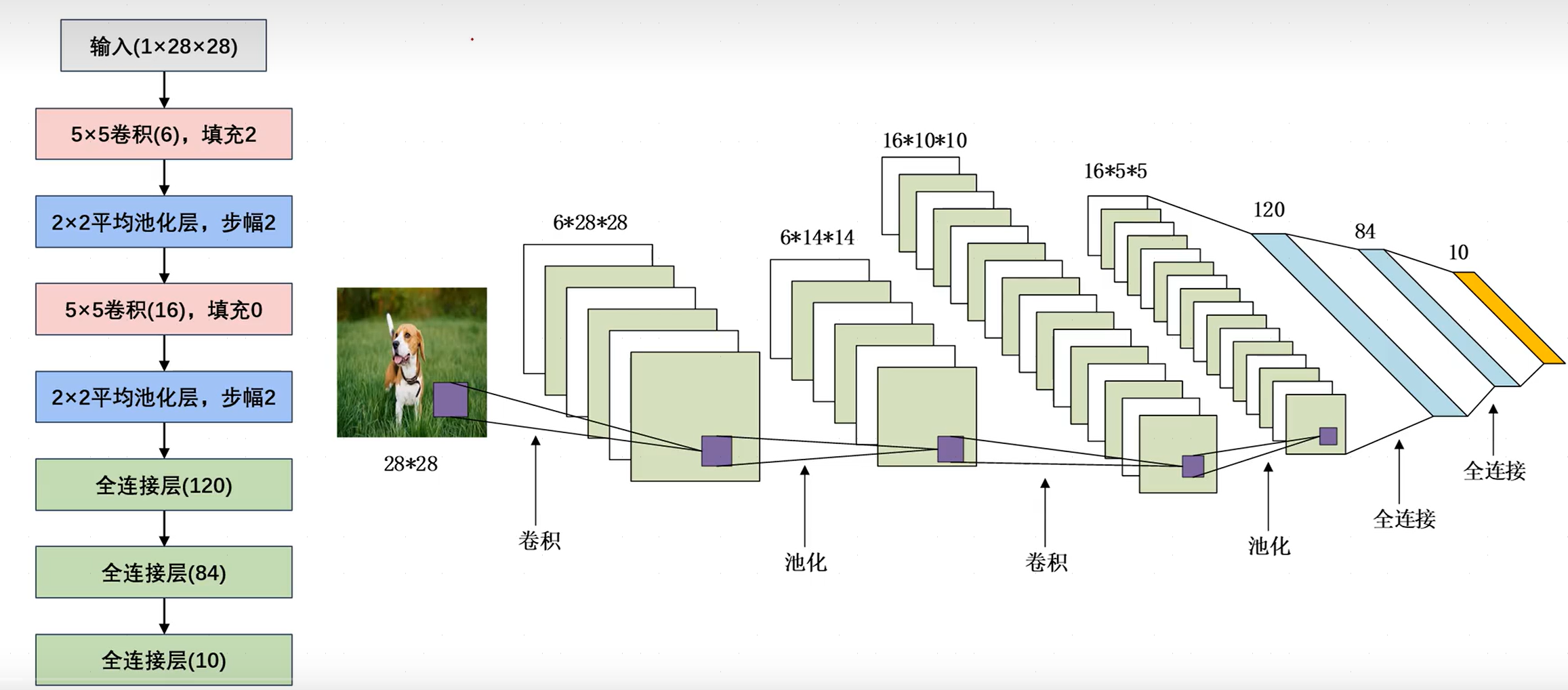
在这里插入图片描述

输入层：输入大小为（28，28）、通道数为1的灰度图像。
卷积层：卷积核尺寸为（6，5，5），即六个5x5大小的卷积核，填充为2，故输出特征图尺寸为（6，28，28）。
池化层：使用平均池化，步幅为2，故输出特征图尺寸为（6，14，14）。
卷积层：卷积核尺寸为（16，6，5，5），即16个6x5x5大小的卷积核，故输出特征图为（16，10，10）.
池化层：使用平均池化，步幅为2，输出特征图为（16，5，5）。
全连接层：将所有特征图均展平为一维向量并进行拼接（通过调用nn.Flatten完成，输出为二维矩阵，每一行向量都是一张图片的展平形式），对应120个神经元。
全连接层：将上一全连接层120个神经元映射为84个神经元。
全连接层：将上一全连接层84个神经元映射为10个神经元。

可知，卷积层往往会使通道数变大，而池化层往往会使特征图尺寸变小。

1.3LeNet5网络总结

在这里插入图片描述

二、AlexNext

在这里插入图片描述

2.1AlexNet网络结构

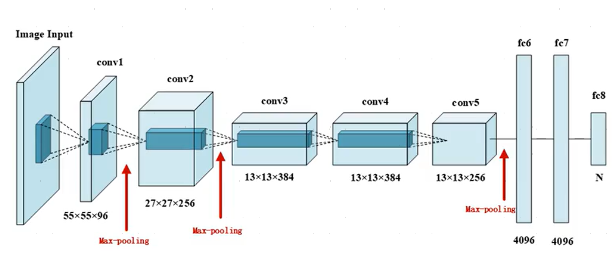
在这里插入图片描述

AlexNet与LeNet设计理念相似，但有如下差异：

AlexNet比LeNet要深很多。
AlexNet由八层组成，包括五个卷积层，两个全连接隐藏层和一个全连接输出层。
AlexNet使用ReLUctant而非sigmoid作为激活函数。

2.2AlexNet网络参数

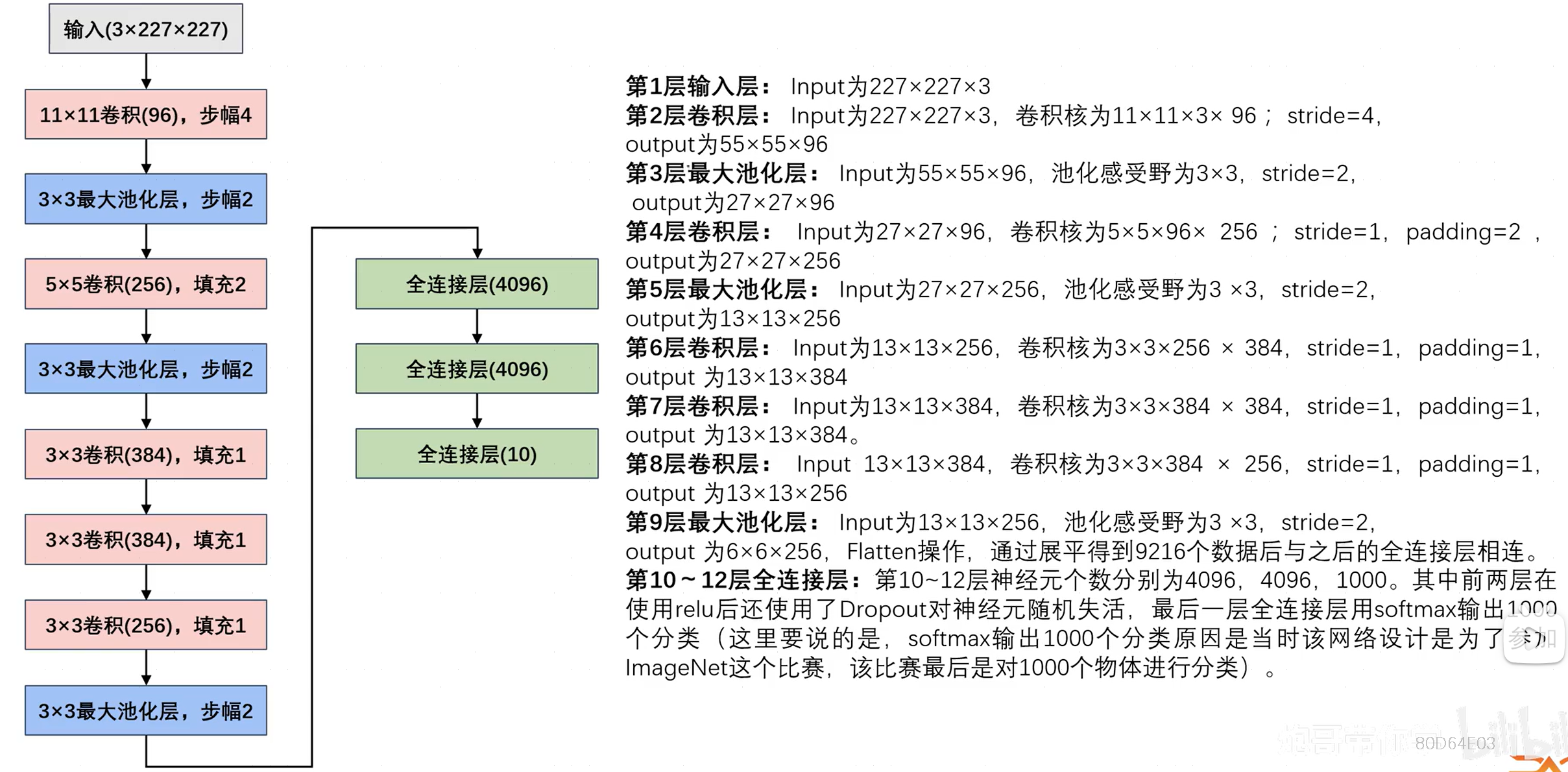
在这里插入图片描述
注意：

图中的数据格式为（H，W，C，N），且最后全连接层的10是因为之后的案例输出为10个分类。
网络参数过多时容易出现过拟合的情况（全连接层存在大量参数 $w 、 b$ ），使用Dropout随机失活神经元。

2.3Dropout操作

Dropout用于缓解卷积神经网络CNN过拟合而被提出的一种正则化方法，它确实能够有效缓解过拟合现象的发生，但是Dropout带来的缺点就是可能会减缓模型收敛的速度，因为每次迭代只有一部分参数更新，可能导致梯度下降变慢。
在这里插入图片描述
其中，神经元的失活仅作用于一轮训练，在下一轮训练时又会随机选择神经元失活。每一轮都会有随机的神经元失活，以此降低缓解过拟合并提高模型训练速度。

2.4PCA图像增强

图像增强是采用一系列技术去改善图像的视觉效果，或将图像转换成一种更适合于人或机器进行分析和处理的形式。例如采用一系列技术有选择地突出某些感兴趣的信息，同时抑制一些不需要的信息，提高图像的使用价值。
在这里插入图片描述

2.5LRN正则化

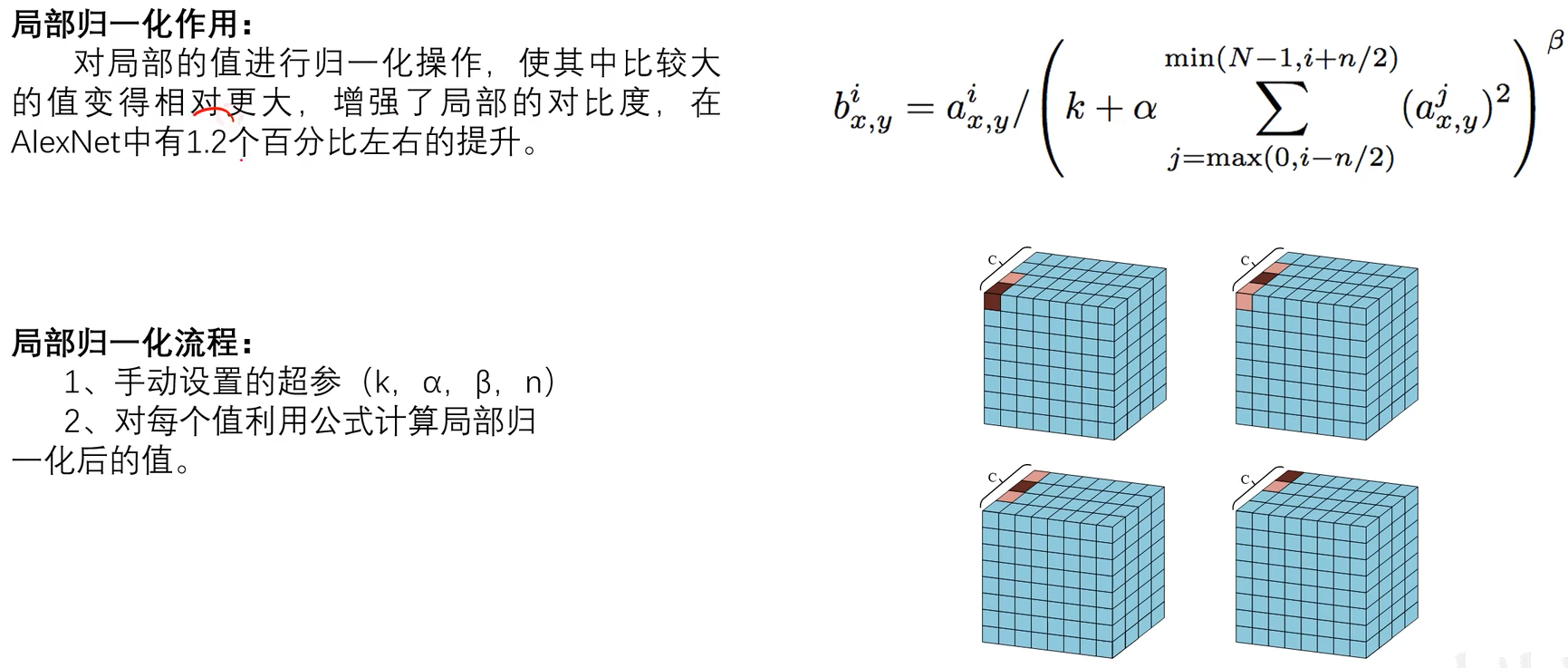
在这里插入图片描述

2.6AlexNet总结

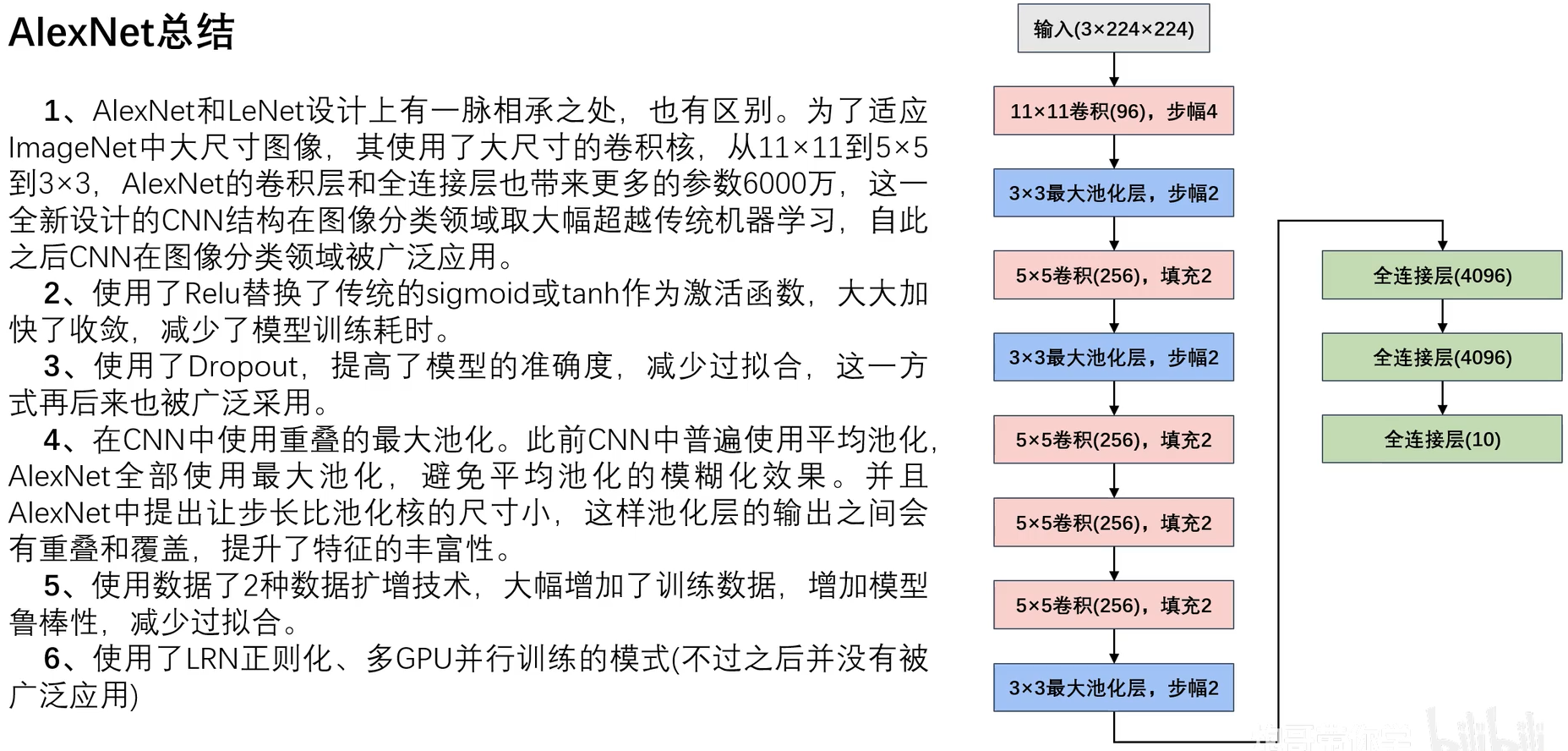
在这里插入图片描述

三、LeNet实战

3.1LeNet5模型搭建

在这里插入图片描述

import torch
from torch import nn
from torchvision.datasets import FashionMNIST
from torchvision import transforms
import matplotlib.pyplot as plt
import numpy as np
import torch.utils.data as Data

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        self.model = nn.Sequential(
            nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2),
            nn.Sigmoid(),
            nn.AvgPool2d(kernel_size=2, stride=2),
            nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),
            nn.AvgPool2d(kernel_size=2, stride=2),
            nn.Flatten(),
            nn.Linear(in_features=16 * 5 * 5, out_features=120),
            nn.Linear(in_features=120, out_features=84),
            nn.Linear(in_features=84, out_features=10),
        )

    def forward(self, x):
        return self.model(x)

myLeNet = LeNet().to(device)
print(summary(myLeNet,input_size=(1, 28, 28)))

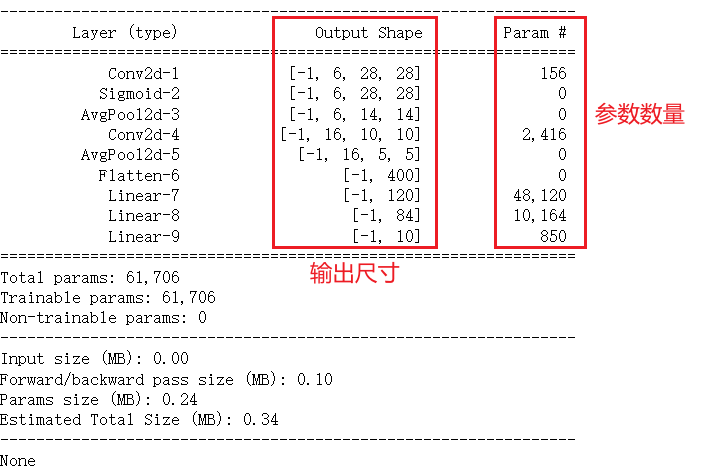
在这里插入图片描述

注意，此处在卷积层后使用了sigmoid激活函数，事实上，卷积操作本质仍是一种线性操作，而若只有线性变换，那无论多少层神经元，都能简化层一层神经元，那神经网络只是简单多元线性回归而已，不能拟合更加复杂的函数。此时使用激活函数就可将神经网络非线性化，即提升神经网络的拟合能力，能拟合更复杂的函数。

3.2可视化数据

加载模型，取出一个batch的数据及标签用于可视化：

train_data = FashionMNIST(root="./", train=True, transform=transforms.ToTensor(), download=True)	# FashionMNIST图像大小为28x28，无需调整
train_loader = Data.DataLoader(dataset=train_data, batch_size=64, shuffle=True)
# 数据可视化
def show_img(train_loader):
    for step, (x, y) in enumerate(train_loader):
        if step > 0:  # 恒成立
            break
    batch_x = x.squeeze().numpy()
    batch_y = y.numpy()
    class_label = train_data.classes
    # 可视化
    fig = plt.figure(figsize=(8, 8))
    for i in range(64):
        ax = fig.add_subplot(8, 8, i + 1, xticks=[], yticks=[])
        ax.imshow(batch_x[i], cmap=plt.cm.binary)
        ax.set_title(class_label[batch_y[i]])
show_img(train_loader)

在这里插入图片描述

3.3加载训练、验证数据集

训练模型：

def train_val_process(train_data, batch_size=128):
    train_data, val_data = Data.random_split(train_data,
                                             lengths=[round(0.8 * len(train_data)), round(0.2 * len(train_data))])
    train_loader = Data.DataLoader(dataset=train_data,
                                   batch_size=batch_size,
                                   shuffle=True,
                                   num_workers=8)
    val_loader = Data.DataLoader(dataset=val_data,
                                 batch_size=batch_size,
                                 shuffle=True,
                                 num_workers=8)
    return train_loader, val_loader


train_dataloader, val_dataloader = train_val_process(train_data)

3.4模型训练

import copy
import time

import torch
from torch import nn
from torchvision.datasets import FashionMNIST
from torchvision import transforms
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import torch.utils.data as Data
def train(model, train_dataloader, val_dataloader, epochs=30, lr=0.001):
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    optimizer = torch.optim.Adam(model.parameters(), lr=lr)
    criterion = nn.CrossEntropyLoss()

    model = model.to(device)
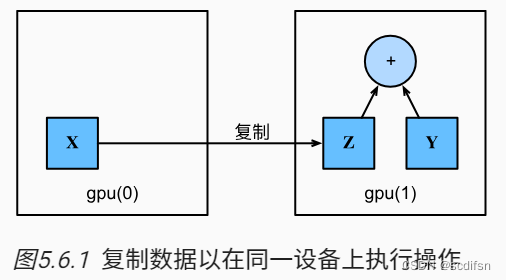
    # 复制当前模型的参数
    best_model_params = copy.deepcopy(model.state_dict())
    # 最高准确率
    best_acc = 0.0
    # 训练集损失函数列表
    train_loss_list = []
    # 验证集损失函数列表
    val_loss_list = []
    # 训练集精度列表
    train_acc_list = []
    # 验证集精度列表
    val_acc_list = []
    # 记录当前时间
    since = time.time()
    for epoch in range(epochs):
        print("Epoch {}/{}".format(epoch + 1, epochs))
        print("-" * 10)
        # 当前轮次训练集的损失值
        train_loss = 0.0
        # 当前轮次训练集的精度
        train_acc = 0.0
        # 当前轮次验证集的损失值
        val_loss = 0.0
        # 当前轮次验证集的精度
        val_acc = 0.0
        # 训练集样本数量
        train_num = 0
        # 验证集样本数量
        val_num = 0
        # 按批次进行训练
        for step, (x, y) in enumerate(train_dataloader):  # 取出一批次的数据及标签
            x = x.to(device)
            y = y.to(device)
            # 设置模型为训练模式
            model.train()
            out = model(x)
            # 查找每一行中最大值对应的行标，即为对应标签
            pre_label = torch.argmax(out, dim=1)
            # 计算损失函数
            loss = criterion(out, y)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            # 累计损失函数，其中，loss.item()是一批次内每个样本的平均loss值(因为x是一批次样本)，乘以x.size(0)，即为该批次样本损失值的累加
            train_loss += loss.item() * x.size(0)
            # 累计精度(训练成功的样本数)
            train_acc += torch.sum(pre_label == y.data)
            # 当前用于训练的样本数量(对应dim=0)
            train_num += x.size(0)
        # 按批次进行验证
        for step, (x, y) in enumerate(val_dataloader):
            x = x.to(device)
            y = y.to(device)
            # 设置模型为验证模式
            model.eval()
            torch.no_grad()
            out = model(x)
            # 查找每一行中最大值对应的行标，即为对应标签
            pre_label = torch.argmax(out, dim=1)
            # 计算损失函数
            loss = criterion(out, y)
            # 累计损失函数
            val_loss += loss.item() * x.size(0)
            # 累计精度(验证成功的样本数)
            val_acc += torch.sum(pre_label == y.data)
            # 当前用于验证的样本数量
            val_num += x.size(0)
        # 计算该轮次训练集的损失值(train_loss是一批次样本损失值的累加，需要除以批次数量得到整个轮次的平均损失值)
        train_loss_list.append(train_loss / train_num)
        # 计算该轮次的精度(训练成功的总样本数/训练集样本数量)
        train_acc_list.append(train_acc.double().item() / train_num)
        # 计算该轮次验证集的损失值
        val_loss_list.append(val_loss / val_num)
        # 计算该轮次的精度(验证成功的总样本数/验证集样本数量)
        val_acc_list.append(val_acc.double().item() / val_num)
        # 打印训练、验证集损失值(保留四位小数)
        print("轮次{} 训练 Loss: {:.4f}, 训练 Acc: {:.4f}".format(epoch+1, train_loss_list[-1], train_acc_list[-1]))
        print("轮次{} 验证 Loss: {:.4f}, 验证 Acc: {:.4f}".format(epoch+1, val_loss_list[-1], val_acc_list[-1]))
        # 如果当前轮次验证集精度大于最高精度，则保存当前模型参数
        if val_acc_list[-1] > best_acc:
            # 保存当前最高准确度
            best_acc = val_acc_list[-1]
            # 保存当前模型参数
            best_model_params = copy.deepcopy(model.state_dict())
            print("保存当前模型参数，最高准确度: {:.4f}".format(best_acc))
        # 训练耗费时间
        time_use = time.time() - since
        print("当前轮次耗时: {:.0f}m {:.0f}s".format(time_use // 60, time_use % 60))
    # 加载最高准确率下的模型参数，并保存模型
    torch.save(best_model_params, "LeNet5_best_model.pth")
    train_process = pd.DataFrame(data={'epoch': range(epochs),
                                       'train_loss_list': train_loss_list,
                                       'train_acc_list': train_acc_list,
                                       'val_loss_list': val_loss_list,
                                       'val_acc_list': val_acc_list
                                       })
    train_process.to_csv("LeNet5_train_process.csv", index=False)
    return train_process
train_process = train(myLeNet, train_dataloader, val_dataloader, epochs=30, lr=0.001)

查看LeNet5_train_process.csv：
在这里插入图片描述

注意，需要使用.double().item()，否则报错TypeError: can‘t convert cuda:0 device type tensor to numpy. Use Tensor.cpu() to copy the tensor。

3.5可视化训练结果

# 训练结果可视化
def train_process_visualization(train_process):
    plt.figure(figsize=(12, 4))
    plt.subplot(1, 2, 1)
    plt.plot(train_process['epoch'], train_process['train_loss_list'], 'ro-', label='train_loss')
    plt.plot(train_process['epoch'], train_process['val_loss_list'], 'bs-', label='val_loss')
    plt.legend()
    plt.xlabel('epoch')
    plt.ylabel('loss')

    plt.subplot(1, 2, 2)
    plt.plot(train_process['epoch'], train_process['train_acc_list'], 'ro-', label='train_acc')
    plt.plot(train_process['epoch'], train_process['val_acc_list'], 'bs-', label='val_acc')
    plt.legend()
    plt.xlabel('epoch')
    plt.ylabel('acc')
    plt.legend()
    plt.show()
train_process_visualization(train_process)

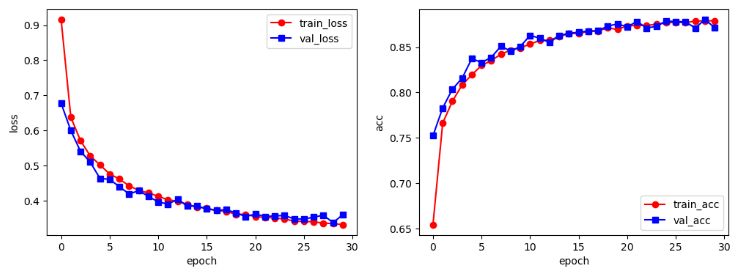
在这里插入图片描述

左图为loss与训练轮次的对应图，右图为acc与训练轮次的对应图。可见，随着训练轮次的增加，损失值不断降低、精确度不断提高。

3.6模型测试

def test(model, test_dataloader, device):
    model.eval()
    test_acc = 0.0
    test_num = 0
    # 推理过程中只前向传播，不用反向传播更新参数，清空梯度节省内存
    torch.no_grad()
    for step, (x, y) in enumerate(test_dataloader):
        x = x.to(device)
        y = y.to(device)
        out = model(x)
        pre_label = torch.argmax(out, dim=1)
        test_acc += torch.sum(pre_label == y.data)
        test_num += x.size(0)
    # 测试集精度
    test_acc = test_acc.double().item() / test_num
    print("测试集精度: {:.4f}".format(test_acc))

model = LeNet()
model = model.to(device)
# 加载模型参数
model.load_state_dict(torch.load("LeNet5_best_model.pth"))
test_data = FashionMNIST(root="./", train=False, transform=transforms.ToTensor(), download=True)
test_dataloader = Data.DataLoader(dataset=test_data, batch_size=64, shuffle=True)
test(model, test_dataloader, device)