目录
前言
一、搜索查找
二、查找算法
1. 线性查找(Linear Search)
2. 二分查找(Binary Search)
3. 插值查找(Interpolation Search)
4. 哈希查找(Hash Search)
5. Fibonacci查找
前言
静态查找算法是在一个静态的数据结构(如数组或列表)中查找特定的元素。这些算法在执行查找操作时不会修改原始数据结构。以下是一些常见的静态查找算法:
顺序查找(Linear Search):
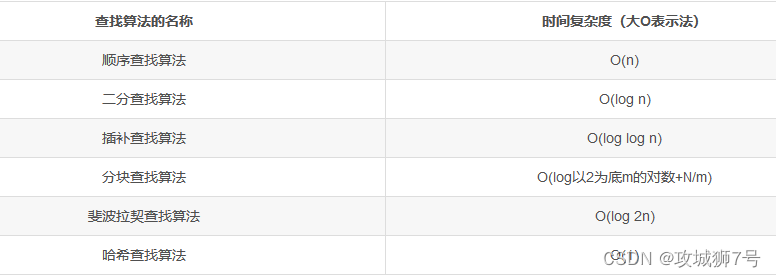
顺序查找是最简单的查找算法。它从数据结构的一端开始,逐个检查每个元素,直到找到所需的元素或到达数据结构的另一端。这种算法的时间复杂度为O(n),其中n是数据结构的长度。
二分查找(Binary Search):
二分查找是一种在有序数组中进行查找的高效算法。它首先将数组的中间元素与目标值进行比较,如果它们相等,则查找成功;如果目标值小于中间元素,则在数组的左半部分继续查找;如果目标值大于中间元素,则在数组的右半部分继续查找。这个过程递归地进行,直到找到目标值或搜索区间为空。二分查找的时间复杂度为O(log n)。
插值查找(Interpolation Search):
插值查找是对二分查找的一种改进,它根据元素的分布情况来调整搜索区间的大小,而不是每次都取中间元素。这种方法在数据分布均匀的情况下比二分查找更高效。
斐波那契查找(Fibonacci Search):
斐波那契查找也是基于二分查找的一种优化算法。它利用了斐波那契数列的性质来划分搜索区间。这种算法适用于均匀分布的数据集,其性能在某些情况下可能优于二分查找。
在选择静态查找算法时,需要考虑数据的特点、规模以及查找的频繁程度。例如,如果数据是静态的且已经排好序,二分查找通常是最有效的选择。如果数据分布不均匀或数据量很大,插值查找或斐波那契查找可能更合适。然而,如果数据量较小或查找不频繁,顺序查找由于实现简单,可能也是一个可行的选择。
一、搜索查找
在数据集合之中,搜索具有特定关键字的结点通常可以根据不同的搜索场景和数据结构分为多种类型。
静态搜索表:
- 定义:当集合中的结点总数是固定的,或者变化非常少时,我们称之为静态搜索表。
- 数据结构:静态搜索表可以是无序的,或者组织成有序表(如数组或有序链表)。
- 搜索策略:对于无序的静态搜索表,通常使用线性搜索;对于有序的静态搜索表,则可以使用二分搜索或其他高效的搜索算法。
动态搜索表:
- 定义:当集合中的结点总数经常发生变化时,我们称之为动态搜索表。
- 数据结构:动态搜索表通常组织成树形结构,如二叉搜索树(BST)、平衡二叉搜索树(如AVL树、红黑树)或B树/B+树等,以适应频繁的插入和删除操作。
- 搜索策略:在树形结构中,搜索通常从根节点开始,根据关键字与节点值的比较结果决定向左子树还是右子树进行搜索,直到找到目标节点或确定不存在为止。
在内存中进行的搜索:
- 重点:由于内存访问速度相对较快,搜索的主要目标是减少比较或查找的次数,以提高搜索效率。
- 评价标准:平均搜索长度(ASL),即从搜索开始到找到目标节点所需比较的平均次数。
在外存中进行的搜索:
- 重点:由于外存(如磁盘)的访问速度远慢于内存,搜索的主要目标是减少访问外存的次数,以降低I/O开销。
- 数据结构:常用的数据结构包括索引文件、倒排索引等,它们通过特定的组织方式将数据与存储位置相关联,以便快速定位数据。
- 评价标准:读盘次数,即从外存中读取数据的次数。由于每次读盘操作都涉及到I/O等待时间,因此减少读盘次数是优化外存搜索性能的关键。
二、查找算法
静态搜索结果采用静态向量(或数组)。
查找算法是计算机科学中一个基础且重要的主题,广泛应用于数据处理和信息检索。本文将介绍几种常见的查找算法,并使用C/C++语言展示它们的实现。
1. 线性查找(Linear Search)
线性查找是最简单的查找算法,适用于未排序的数据集。它逐一检查数据集中的每个元素,直到找到目标值或遍历完所有元素。
#include <stdio.h>
int linearSearch(int arr[], int n, int x) {
for (int i = 0; i < n; i++) {
if (arr[i] == x) {
return i; // 返回找到的元素的索引
}
}
return -1; // 如果没有找到,返回-1
}
int main() {
int arr[] = {2, 3, 4, 10, 40};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 10;
int result = linearSearch(arr, n, x);
(result == -1) ? printf("元素不在数组中") : printf("元素在索引 %d", result);
return 0;
}2. 二分查找(Binary Search)
二分查找是一种高效的查找算法,但要求数据集必须是有序的。它通过反复将查找范围减半来快速定位目标值。
#include <stdio.h>
// 二分查找算法
// arr[] 是一个升序排列的数组
// l 是要搜索的范围的左端点
// r 是要搜索的范围的右端点
// x 是要搜索的元素
int binarySearch(int arr[], int l, int r, int x) {
while (l <= r) {
// 防止 (l + r) 的和超过 int 的最大值
int m = l + (r - l) / 2;
// 检查中间元素
if (arr[m] == x) {
return m; // 元素找到,返回索引
}
// 如果中间元素小于x,忽略左半边
if (arr[m] < x) {
l = m + 1;
}
// 如果中间元素大于x,忽略右半边
else {
r = m - 1;
}
}
return -1; // 元素不在数组中,返回-1
}
int main() {
int arr[] = {2, 3, 4, 10, 40}; // 输入数组
int n = sizeof(arr) / sizeof(arr[0]); // 计算数组中的元素个数
int x = 10; // 要查找的元素
int result = binarySearch(arr, 0, n - 1, x); // 调用二分查找算法
// 输出结果
if (result == -1) {
printf("元素不在数组中");
} else {
printf("元素在索引 %d", result);
}
return 0;
}
3. 插值查找(Interpolation Search)
插值查找是二分查找的改进版本,适用于均匀分布的有序数据集。它通过估计目标值的位置来减少查找范围。
#include <stdio.h>
// 插值查找算法
// arr[] 是一个升序排列的数组
// n 是数组中元素的数量
// x 是要搜索的元素
int interpolationSearch(int arr[], int n, int x) {
int lo = 0, hi = (n - 1);
// 当待搜索的区段有效,并且目标值在[lo, hi]区间内时,执行搜索
while (lo <= hi && x >= arr[lo] && x <= arr[hi]) {
// 如果lo和hi相等,只需检查lo位置的元素
if (lo == hi) {
if (arr[lo] == x) return lo; // 找到目标值
return -1; // 没有找到目标值
}
// 计算可能的位置pos,使用插值公式
int pos = lo + (((double)(hi - lo) / (arr[hi] - arr[lo])) * (x - arr[lo]));
// 如果找到了目标值,返回其索引
if (arr[pos] == x) {
return pos;
}
// 如果目标值大于pos位置的元素,调整lo
if (arr[pos] < x) {
lo = pos + 1;
}
// 如果目标值小于pos位置的元素,调整hi
else {
hi = pos - 1;
}
}
return -1; // 如果没有找到目标值,返回-1
}
int main() {
int arr[] = {2, 3, 4, 10, 40}; // 输入数组
int n = sizeof(arr) / sizeof(arr[0]); // 计算数组中的元素个数
int x = 10; // 要查找的元素
int result = interpolationSearch(arr, n, x); // 调用插值查找算法
// 输出查找结果
if (result == -1) {
printf("元素不在数组中");
} else {
printf("元素在索引 %d", result);
}
return 0;
}
4. 哈希查找(Hash Search)
哈希查找利用哈希表来存储数据,通过计算键的哈希值来快速定位数据。哈希表的实现较为复杂,通常使用标准库中的哈希表数据结构。
#include <iostream>
#include <unordered_map>
int main() {
// 创建一个unordered_map来存储数组元素和它们的索引
std::unordered_map<int, int> hashMap;
// 初始化数组
int arr[] = {2, 3, 4, 10, 40};
// 计算数组中的元素数量
int n = sizeof(arr) / sizeof(arr[0]);
// 将数组元素及其索引存入哈希表
for (int i = 0; i < n; i++) {
hashMap[arr[i]] = i;
}
// 要查找的元素
int x = 10;
// 在哈希表中查找元素
auto it = hashMap.find(x);
// 根据查找结果输出信息
if (it != hashMap.end()) {
// 如果元素在哈希表中,输出它的索引
std::cout << "元素在索引 " << it->second << std::endl;
} else {
// 如果元素不在哈希表中,输出相应信息
std::cout << "元素不在数组中" << std::endl;
}
return 0;
}
5. Fibonacci查找
Fibonacci查找算法是一种基于Fibonacci数列的查找算法,它类似于二分查找,但使用Fibonacci数列来确定查找范围的分割点。这种算法适用于有序数组,并且可以在某些情况下比二分查找更高效。
#include <iostream>
#include <algorithm> // 用于std::min函数
// 斐波那契查找算法
// arr[] 是一个升序排列的数组
// n 是数组中元素的数量
// x 是要搜索的元素
int fibonacciSearch(int arr[], int n, int x) {
// 初始化斐波那契数列
int fibMMm2 = 0; // (m-2)'th 斐波那契数
int fibMMm1 = 1; // (m-1)'th 斐波那契数
int fibM = fibMMm2 + fibMMm1; // m'th 斐波那契数
// 找到最小的斐波那契数,该数大于或等于n
while (fibM < n) {
fibMMm2 = fibMMm1;
fibMMm1 = fibM;
fibM = fibMMm2 + fibMMm1;
}
// 标记已经检查过的元素的偏移量
int offset = -1;
// 当还有斐波那契数剩余时,执行查找
while (fibM > 1) {
// 检查fibMMm2是否为有效位置
int i = std::min(offset + fibMMm2, n - 1);
// 如果x大于当前位置的元素,剪切数组的后半部分
if (arr[i] < x) {
fibM = fibMMm1;
fibMMm1 = fibMMm2;
fibMMm2 = fibM - fibMMm1;
offset = i;
}
// 如果x小于当前位置的元素,剪切数组的前半部分
else if (arr[i] > x) {
fibM = fibMMm2;
fibMMm1 -= fibMMm2;
fibMMm2 = fibM - fibMMm1;
}
// 如果找到了x,返回索引
else {
return i;
}
}
// 检查最后一个元素是否为x
if (fibMMm1 && arr[offset + 1] == x) {
return offset + 1;
}
// 如果未找到元素,返回-1
return -1;
}
int main() {
// 初始化数组
int arr[] = {10, 22, 35, 40, 45, 50, 80, 82, 85, 90, 100};
// 计算数组中的元素数量
int n = sizeof(arr) / sizeof(arr[0]);
// 要查找的元素
int x = 85;
// 调用斐波那契查找算法
int result = fibonacciSearch(arr, n, x);
// 输出查找结果
if (result == -1) {
std::cout << "Element not found" << std::endl;
} else {
std::cout << "Element found at index " << result << std::endl;
}
return 0;
}
-
初始化Fibonacci数列:首先,我们初始化Fibonacci数列的三个连续的Fibonacci数:
fibMMm2(第(m-2)个Fibonacci数),fibMMm1(第(m-1)个Fibonacci数),和fibM(第m个Fibonacci数)。 -
找到最小的Fibonacci数:我们找到最小的Fibonacci数,该数大于或等于数组的长度
n。 -
缩小查找范围:使用Fibonacci数列来确定查找范围的分割点。如果目标值
x大于当前元素,则向右移动Fibonacci数列;如果x小于当前元素,则向左移动Fibonacci数列。 -
检查最后一个元素:在循环结束后,检查最后一个元素是否为目标值。
-
返回结果:如果找到目标值,返回其索引;否则返回-1。
Fibonacci查找算法在某些情况下可以比二分查找更高效,尤其是在数组长度接近Fibonacci数时。