使用语义熵检测大语言模型中的幻觉
- Detecting hallucinations in large language models using semantic entropy 论文阅读
- 摘要
- 研究目标
- 论文图表概述
- 总结
- 关键解决方案
- 语义熵计算:
- 虚构内容检测:
- 双向蕴涵
- 在大语言模型中的应用
- 上下文的重要性
- 蕴涵估计器
- 实验设计
- 语义熵计算步骤
- 结果分析
- AUROC 和 AURAC
- 总结
- 评估指标
Detecting hallucinations in large language models using semantic entropy 论文阅读
作者: Sebastian Farquhar, Jannik Kossen, Lorenz Kuhn, Yarin Gal
发表日期: 2024年6月20日
原文
摘要
大语言模型(LLM)如ChatGPT和Gemini在推理和问答方面表现出色,但经常产生错误输出或未经证实的答案,被称为“幻觉”。这些幻觉在法律、新闻和医学等领域带来了可靠性问题,导致错误信息传播和潜在的严重后果。本文提出了一种基于熵的统计方法,用于检测大型语言模型(LLM)中的“虚构内容”(confabulations),即生成的任意且错误的信息。通过计算生成内容的语义熵,该方法能够在不同任务和数据集中检测虚构内容,不需要任务特定的数据,具有良好的泛化能力。
研究目标
开发一种通用的、有效的方法,用于检测大型语言模型(LLM)生成的虚构内容,从而确保其输出在多样化领域中的可靠性。该方法不依赖任务的先验知识,能够跨数据集和任务通用,显示出较强的鲁棒性和通用性。不同于传统的基于词序列的熵计算方法,本文方法计算生成内容的语义熵,即在语义层面对生成内容进行聚类,从而更准确地检测虚构内容。
论文图表概述
图 1 语义熵和虚构检测概述
-
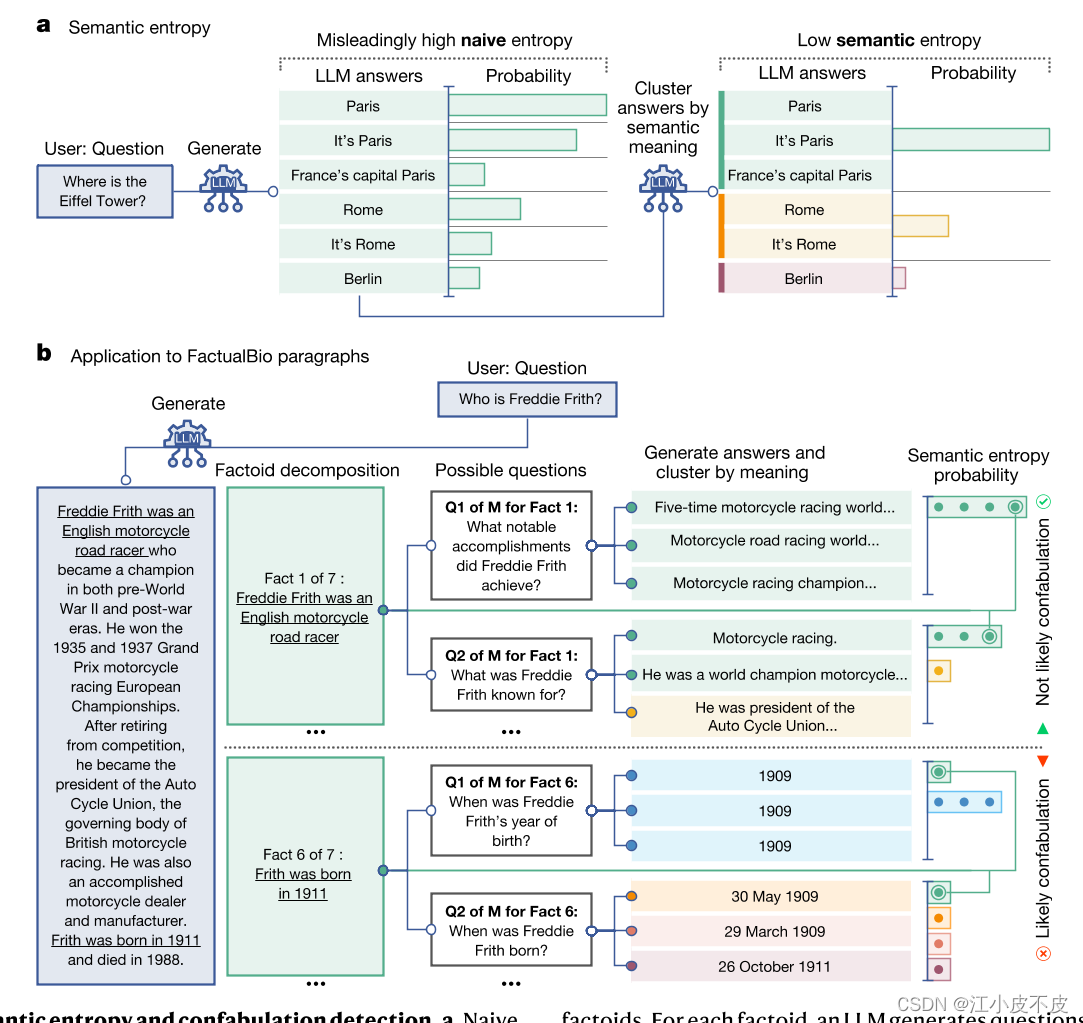
a. 语义熵的概念示意图
- 图中左侧展示了传统的熵计算方法,这种方法基于具体答案的变化来衡量不确定性,容易导致高熵值,因为不同的答案形式尽管意思相同,但会被视为不同的答案。
- 图中右侧展示了语义熵的方法,通过将语义相同的答案聚类来计算不确定性。这种方法将相同语义的答案归为一类,避免了因词语变化带来的不确定性。
- 基于朴素熵的不确定性衡量中,将“巴黎”、“法国巴黎”和“法国首都巴黎”视为不同答案。但在某些语言任务中,不同的答案可能意味着相同的事物。
-
b. 语义熵在长段落中的应用
- 图中展示了如何将长段落分解为具体的事实性命题,每个命题再生成相关的问题,并通过模型生成多个答案。
- 最后,通过计算这些答案的语义熵来判断每个命题是否为幻觉。
- 在这里,语义熵将 Fact 1 分类为非虚构,因为尽管生成的答案措辞不同,但它们的意义相同,而朴素熵可能会忽略这一点。
图 2 检测句子长度中的虚构
- 图表解释
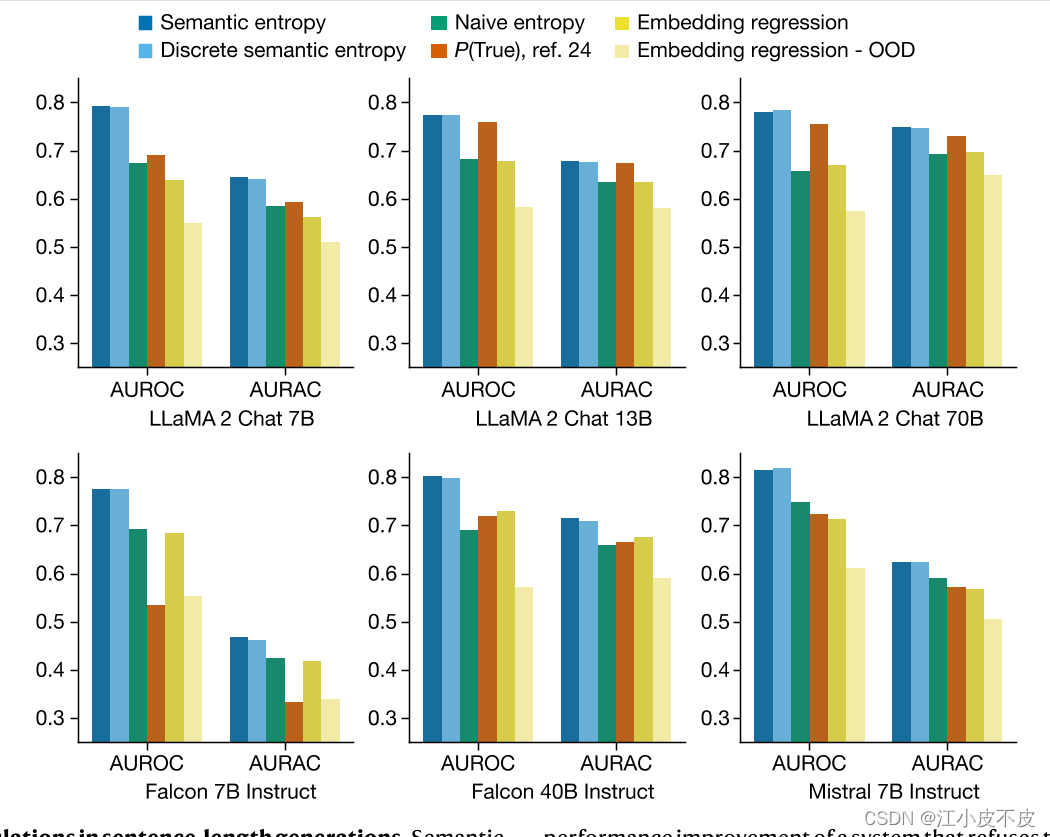
- 图表展示了在不同模型(如LLaMA 2 Chat 7B、13B、70B和Falcon 7B、40B等)上,语义熵和其他基准方法(如朴素熵、P(True)和嵌入回归)的AUROC(接收者操作特征曲线下面积)和AURAC(拒绝准确性曲线下面积)指标。
- AUROC衡量了方法预测错误答案的可靠性,分数范围从0到1,1代表完美分类器,0.5代表无信息分类器。
- AURAC衡量了在模型拒绝回答可能产生幻觉的问题后剩余问题的回答准确性,分数越高,表示过滤掉幻觉问题后模型的回答更准确。
- 结果显示,语义熵在所有模型和数据集上的AUROC和AURAC均显著优于其他基准方法,表明语义熵方法在检测幻觉和提高问答准确性方面表现出色。
图 3 离散语义熵在段落长度传记生成中的效果
- 图表解释
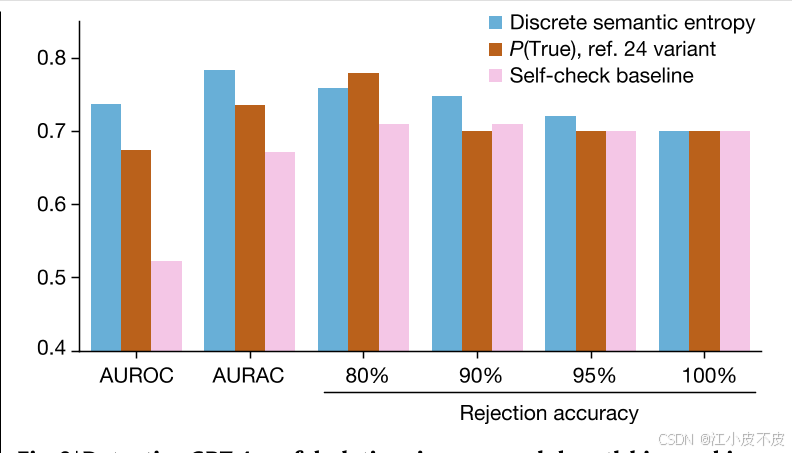
- 图3展示了在GPT-4生成的传记文本中,离散语义熵方法相对于基准方法(如P(True)变体和自检基线)的AUROC和AURAC表现。图表的横轴表示不同模型及不同评估指标,纵轴表示性能得分。
- 左侧(AUROC):展示了离散语义熵方法和其他基准方法在传记生成任务中的AUROC表现。
- 语义熵方法(包括离散语义熵)表现明显优于其他基准方法(如P(True)和自检基线)。
- 这一结果表明,离散语义熵方法在检测传记文本中的幻觉方面更为有效。
- 右侧(AURAC):展示了在不同拒绝比例下,离散语义熵方法和其他基准方法的AURAC表现。
- 离散语义熵方法在绝大多数拒绝比例下(80%-100%)的回答准确性最高。
- 仅在拒绝比例达到20%的情况下,P(True)基线略有优势。
- 这表明离散语义熵方法能够有效拒绝潜在的幻觉内容,显著提高剩余回答的准确性。
表1 语义熵和朴素熵预测
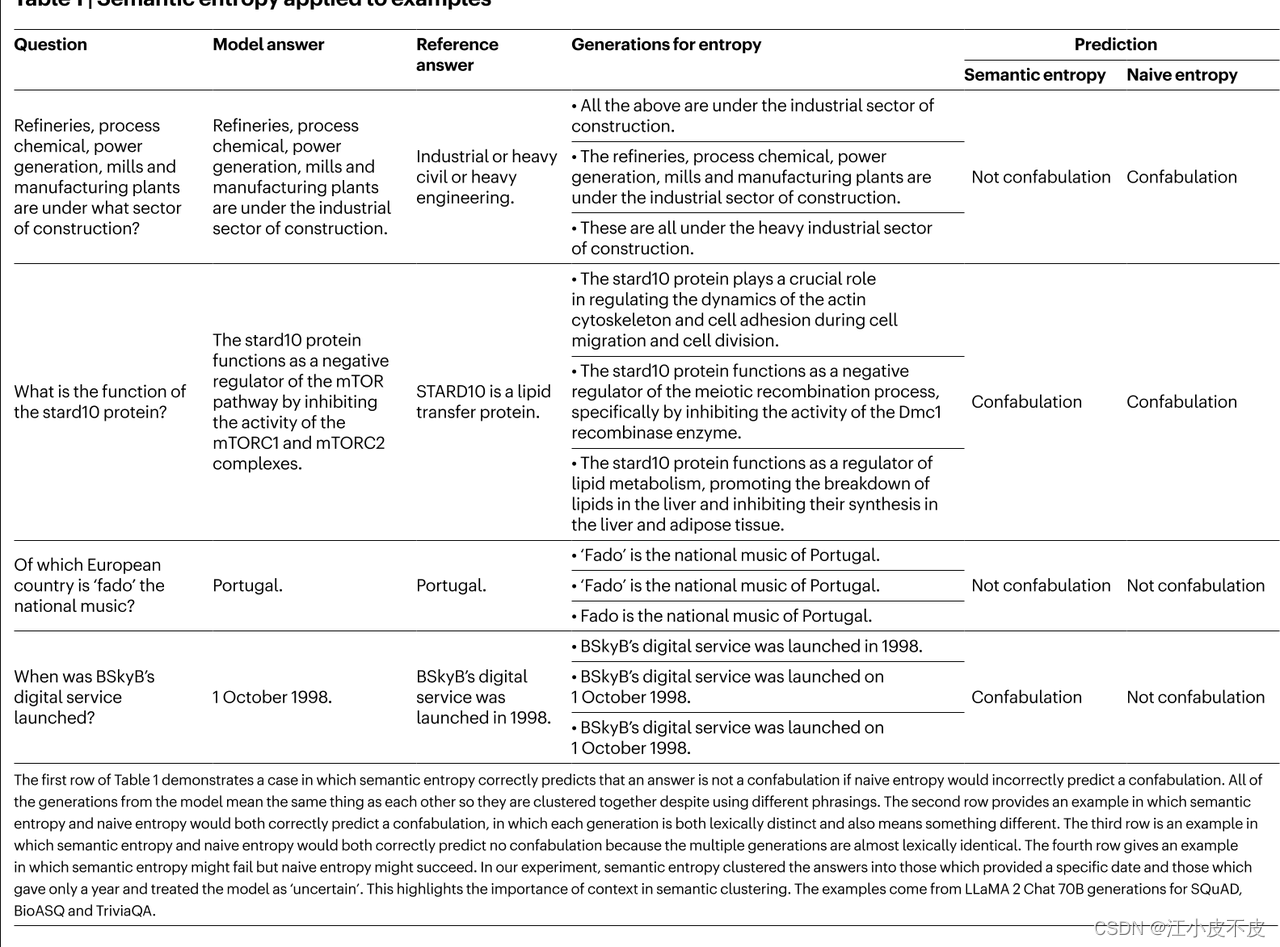
- 表格结构和内容
- 问题:问题的陈述。
- 模型答案:由模型生成的答案。
- 参考答案:被认为是正确答案的参考。
- 熵的生成:由模型生成的多种答案,用于计算语义熵和朴素熵。
- 预测:根据语义熵和朴素熵预测的结果是否是虚假信息。
第一个例子(关于工业部门):
- 问题: Refineries process chemical power generation mills and manufacturing plants are under what sector of construction?
- 模型答案: 与参考答案一致,属于工业部门。
- 生成的答案: 多种答案都与工业部门有关。
- 预测: 语义熵预测为非虚假信息,朴素熵预测为虚假信息。
第二个例子(关于stard10蛋白的功能):
- 问题: What is the function of the stard10 protein?
- 模型答案: 负调控mTOR通路。
- 参考答案: 是脂质转移蛋白。
- 生成的答案: 各种不同的功能描述。
- 预测: 语义熵和朴素熵均预测为虚假信息。
第三个例子(关于“fado”音乐):
- 问题: Which European country is ‘fado’ the national music of?
- 模型答案: 葡萄牙。
- 参考答案: 葡萄牙。
- 生成的答案: 一致地回答“葡萄牙”。
- 预测: 语义熵和朴素熵均预测为非虚假信息。
第四个例子(关于BSkyB的数字服务上线时间):
- 问题: When was BSkyB’s digital service launched?
- 模型答案: 1998年10月1日。
- 参考答案: 1998年。
- 生成的答案: 一致地回答具体的日期和年份。
- 预测: 语义熵预测为虚假信息,朴素熵预测为非虚假信息。
总结
语义熵: 通过多样性和上下文理解来判断答案是否是虚假信息。
朴素熵: 通过简单的答案相似度来判断答案是否是虚假信息。
表格显示了语义熵在某些情况下能够更好地预测答案的真实性,因为它能够更好地理解语义和上下文,而朴素熵可能会因为缺乏上下文理解而做出错误的预测。
关键解决方案
语义熵计算:
- 多次生成回答并对这些回答进行语义聚类。
- 使用双向蕴涵关系(bidirectional entailment)进行语义聚类,即判断两个回答在语义上是否互相蕴涵。
- 计算生成内容的语义熵,熵值越高,表示不确定性越高,虚构内容的可能性也越高。
虚构内容检测:
- 根据计算出的语义熵,判断生成内容是否可能是虚构的。
- 提高问答模型的准确性,避免使用高熵值的不可靠回答。
双向蕴涵
双向蕴涵是自然语言处理和逻辑推理中的一个概念,用于判断两个句子在意义上的等价性。具体来说,双向蕴涵表示如果一个句子的意义能够推出另一个句子的意义,反之亦然,那么这两个句子在语义上是等价的。
- 单向蕴涵(Unidirectional Entailment): 如果句子A的真值可以推出句子B的真值,我们说句子A蕴涵句子B。例如,句子“A是猫”蕴涵句子“A是动物”,因为如果A是猫,那么A必然是动物。
- 双向蕴涵(Bidirectional Entailment): 如果句子A蕴涵句子B,同时句子B也蕴涵句子A,我们说句子A和句子B是双向蕴涵的。例如,句子“A是巴黎的首都”和“巴黎是法国的首都”之间存在双向蕴涵,因为它们在意义上是等价的。
在大语言模型中的应用
在大语言模型(LLM)中,双向蕴涵用于检测生成内容的语义一致性,特别是在检测虚构内容时。具体应用步骤如下:
- 生成多个答案: 对于一个给定的问题,生成多个可能的答案。
- 语义聚类: 使用双向蕴涵判断这些答案是否在语义上等价,并将等价的答案聚为一类。
- 方法: 利用自然语言推理(NLI)工具或预训练语言模型(如GPT-3或DeBERTa)来判断两个句子之间是否存在蕴涵关系。如果两个句子互相蕴涵,则认为它们在语义上等价。
- 计算语义熵: 通过统计不同语义类的概率分布,计算生成内容的语义熵,从而评估生成内容的可靠性。
上下文的重要性
上下文在双向蕴涵中起着至关重要的作用。例如,单独的词“巴黎”并不蕴涵“法国的首都是巴黎”,因为“巴黎”不是一个完整的陈述句。然而,在问题“法国的首都是什么?”的上下文中,“巴黎”可以蕴涵“法国的首都是巴黎”。
例如:
- 问题: “法国的首都是什么?”
- 简短回答: “巴黎。”
- 详细回答: “法国的首都是巴黎。”
在这个上下文中,简短回答和详细回答在意义上是等价的,简短回答蕴涵了详细回答的全部意义。
蕴涵估计器
例如 LLaMA 2、GPT-3.5 (Turbo 1106) 或 GPT-4来预测各代之间的蕴涵。我们使用以下提示:
我们正在评估对于问题 {question}的答案。这里有两个可能的答案:
可能的答案 1:{text1}
可能的答案 2:{text2}
可能的答案 1 在语义上是否蕴含可能的答案 2?用蕴含、矛盾或中性来回答。
We are evaluating answers to the question {question}
Here are two possible answers:
Possible Answer 1: {text1}
Possible Answer 2: {text2}
Does Possible Answer 1 semantically entail Possible Answer 2? Respond with entailment, contradiction, or neutral.
实验设计
数据集:
- TriviaQA:涵盖广泛的知识问答。
- SQuAD 1.1:基于维基百科的阅读理解数据集。
- BioASQ:生物医学领域的问题回答数据集。
- NQ-Open:来自谷歌搜索的自然问题数据集。
- SVAMP:数学词问题数据集。
- FactualBio:传记生成数据集。
模型:
- 使用了LLaMA 2 Chat(7B、13B和70B参数)、Falcon Instruct(7B和40B参数)和Mistral Instruct(7B参数)等多个模型进行实验。
语义熵计算步骤
- 生成:从LLM的预测分布中采样生成多个答案序列。
- 聚类:使用双向蕴涵关系进行语义聚类,将语义相同的答案归为一类。
- 熵估计:计算语义聚类后的概率分布,并根据该分布计算语义熵。
结果分析
语义熵方法在多种数据集和模型上均表现优异,能够有效检测虚构内容并提高问答准确性。
AUROC 和 AURAC
AUROC:
- 定义:
- AUROC 是指接收者操作特征曲线(ROC曲线)下的面积。ROC曲线绘制了模型的真阳性率(TPR,也称为召回率)对假阳性率(FPR)的关系。
- 计算方法:
- 真阳性率(TPR):在所有实际为正的样本中,被正确预测为正的比例。计算公式为:TPR = TP / (TP + FN),其中TP为真阳性,FN为假阴性。
- 假阳性率(FPR):在所有实际为负的样本中,被错误预测为正的比例。计算公式为:FPR = FP / (FP + TN),其中FP为假阳性,TN为真阴性。
- 通过改变分类模型的阈值,可以得到一系列的TPR和FPR值,并绘制出ROC曲线。AUROC 是ROC曲线下的面积,数值范围在0到1之间。
- 意义:
- AUROC 值越接近1,表示模型的分类性能越好。
- AUROC 值为0.5,表示模型没有区分能力,相当于随机猜测。
- AUROC 值小于0.5,表示模型的分类能力比随机猜测还差,可能存在某些问题。
- 解释:
- 在本文中,AUROC 衡量了语义熵方法预测模型错误答案的可靠性,较高的AUROC值表明语义熵方法能够有效区分正确和错误的模型生成。
AURAC(拒绝准确性曲线下面积):
- 定义:
- AURAC 是指拒绝准确性曲线(Rejection Accuracy Curve)下的面积。拒绝准确性曲线绘制了模型拒绝回答可能产生幻觉的问题后,剩余问题的回答准确性。
- 计算方法:
- 拒绝准确性:在模型拒绝回答部分问题后,剩余问题的回答准确性。
- 随着拒绝比例的增加,模型剩余回答的准确性通常会提高,因为被拒绝的问题往往是模型不确定或容易产生幻觉的问题。
- 通过改变拒绝的阈值,可以得到一系列的拒绝准确性值,并绘制出拒绝准确性曲线。AURAC 是该曲线下的面积,数值范围同样在0到1之间。
- 意义:
- AURAC 值越高,表示模型在拒绝不确定回答后,剩余回答的准确性越高。
- AURAC 值能够综合反映模型在不同拒绝阈值下的整体表现。
- 在本文中,AURAC 衡量了语义熵方法通过拒绝回答不确定问题后,提升剩余回答准确性的效果。较高的AURAC值表明语义熵方法能够有效识别并拒绝潜在幻觉内容,显著提高模型回答的总体准确性。
总结
AUROC 和 AURAC 是评估语义熵方法性能的重要指标,前者侧重于模型预测错误答案的能力,后者则评估模型在拒绝不确定回答后的准确性提升。本文通过这些指标展示了语义熵方法在检测和减少大语言模型幻觉内容方面的优越性能。
评估指标
语义熵(Semantic Entropy):
- 语义熵是用于检测大语言模型(LLM)输出不确定性的一种方法。其核心思想是根据生成文本的意义而非具体的词序列来计算不确定性。具体步骤如下:
- 对输入生成多个答案。
- 使用双向蕴涵(entailment)方法将这些答案聚类,根据答案是否在语义上等价进行分组。
- 计算这些语义等价群组的概率分布,从而估算生成文本的语义熵。高语义熵表示模型对生成的内容存在高不确定性,可能产生虚构内容。
离散语义熵(Discrete Semantic Entropy):
- 离散语义熵是语义熵的一种变体,主要用于在无法获得模型输出概率的情况下使用。其基本思想是将生成的答案视为离散的类别,通过统计各类别出现的频率来估计概率分布。
- 生成多个答案。
- 使用同样的方法将答案进行语义聚类。
- 计算每个语义等价群组的频率,作为其概率分布,从而估算语义熵。
朴素熵(Naive Entropy):
- 朴素熵直接基于生成的词序列计算不确定性。其计算方式是基于词的联合概率分布:
- 对生成的每个答案,计算其词序列的联合概率。
- 将这些概率归一化后,计算整个生成序列的熵。由于未考虑语义等价性,这种方法可能高估了不确定性。
P(True):
- P(True)方法是一种基于生成答案的可信度估计方法。其具体步骤如下:
- 生成多个答案,并将这些答案列表以及最可能的答案提供给模型。
- 让模型判断最可能的答案是否为真,并计算其回答“是”的概率作为可信度分数。
- 使用少量训练数据(few-shot)来增强模型对问题的理解和回答的准确性。
嵌入回归(Embedding Regression):
- 嵌入回归是一种监督学习方法,用于预测模型回答的正确性。其基本步骤如下:
- 使用语言模型生成答案并获取其最后的隐藏状态(嵌入)。
- 训练一个逻辑回归分类器,基于这些嵌入来预测答案是否正确。
- 这种方法依赖于训练数据的分布,如果训练数据和实际应用中的数据分布不匹配,性能可能会下降。
嵌入回归 - 分布外(Embedding Regression - OOD):
- 分布外(Out-of-Distribution OOD)嵌入回归方法与嵌入回归类似,但训练数据和测试数据来自不同分布。
- 训练分类器时使用一种数据分布,评估时使用另一种不同的数据分布。
- 这种情况下,模型的性能通常会显著下降,因为训练时学到的模式可能无法很好地泛化到新的数据分布。