Overview

从上图可以看见，整个强化学习被分为两个板块：一个是基础的工具，一个是基本的算法和方法。

基础工具包括：基本的概念、贝尔曼公式、贝尔曼最优公式。

算法和方法包括：值迭代、策略迭代、蒙特卡洛方法、时序差分的方法等等。

后面章节都是以前面章节的概念和思路为基础的。

强化学习的最终目标就是在求解最优策略。

第一章：基本概念

State 和 State Space

State 其实描述的就是 agent 相对于环境的一个状态。

在上图的 grid-world 例子中，每一个二维平面上的位置就是一个状态 Si，但这是一个抽象的表示，这里是化繁为简，如果是更复杂的问题，那么 Si 除了位置之外，可能还有速度啊、加速度等等相关的状态信息，这些也是状态的一部分。

而 State Space 状态空间就是所有这些状态的集合。

Action

在每一个状态下，实际上都是有一系列的可采取的行动。

这些所有的行动放在一起就得到了一个集合，称为 Action space of a state。

值得注意的是，我们的行为空间和状态是依赖关系，对于不同的状态，它的 action space 是不一样的。

这也是为什么上图在用数学表示 action space 时使用 A(Si) 。

State transition

State transition 实际上是定义了 agent 和环境的一种交互的行为。

State transition 可以使用下面 表格 的形式展现出来：

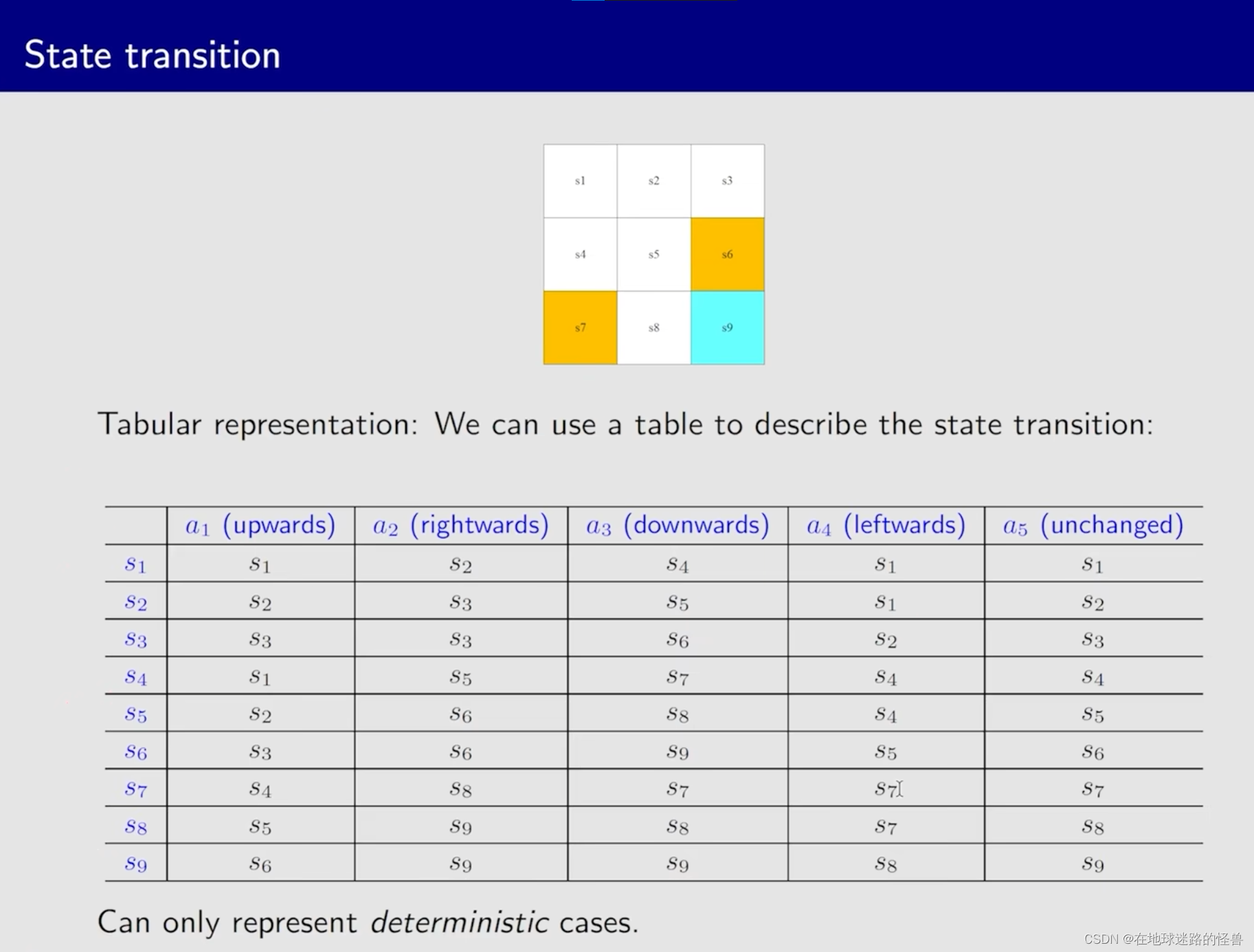
但是表格只能表示出这种 deterministic 确定性的情况，对于有多个状态存在这样的多可能性表格就不再适用（比如 s1 选择 a1 之后可能会进入到 s1 状态，也可能进入到 s4 状态，甚至是 s7 状态）。

更一般的方法是使用 State transition probability 来进行描述：

数学上使用 conditional probability 条件概率来描述上图的行为。

条件概率也比较简单，对于上图中的这两个条件概率公式：

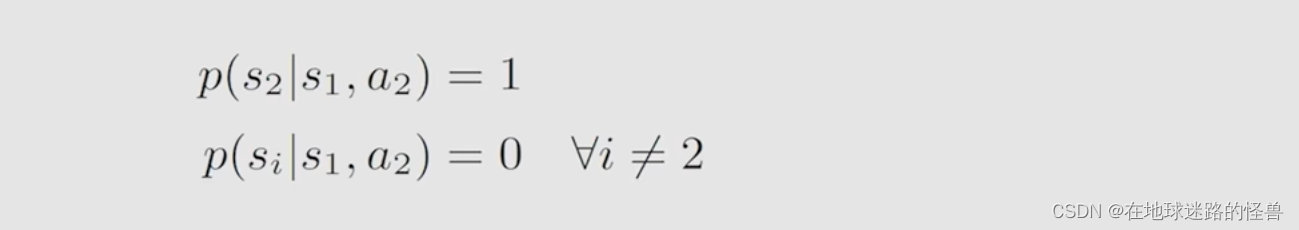
其第一行式子含义表示 ：如果现在我处于 s1，并且现在 take action a2 的话，那么下一个时刻跳到 s2 的概率就是 1。同理对于第二行表达式来说，其表示如果当前处于 s1， 采取行动 a2 的话，跳到 si （i不为2，也就是跳到其它状态）的概率为 0。

这就是用条件概率来描述 State transition 。

Policy

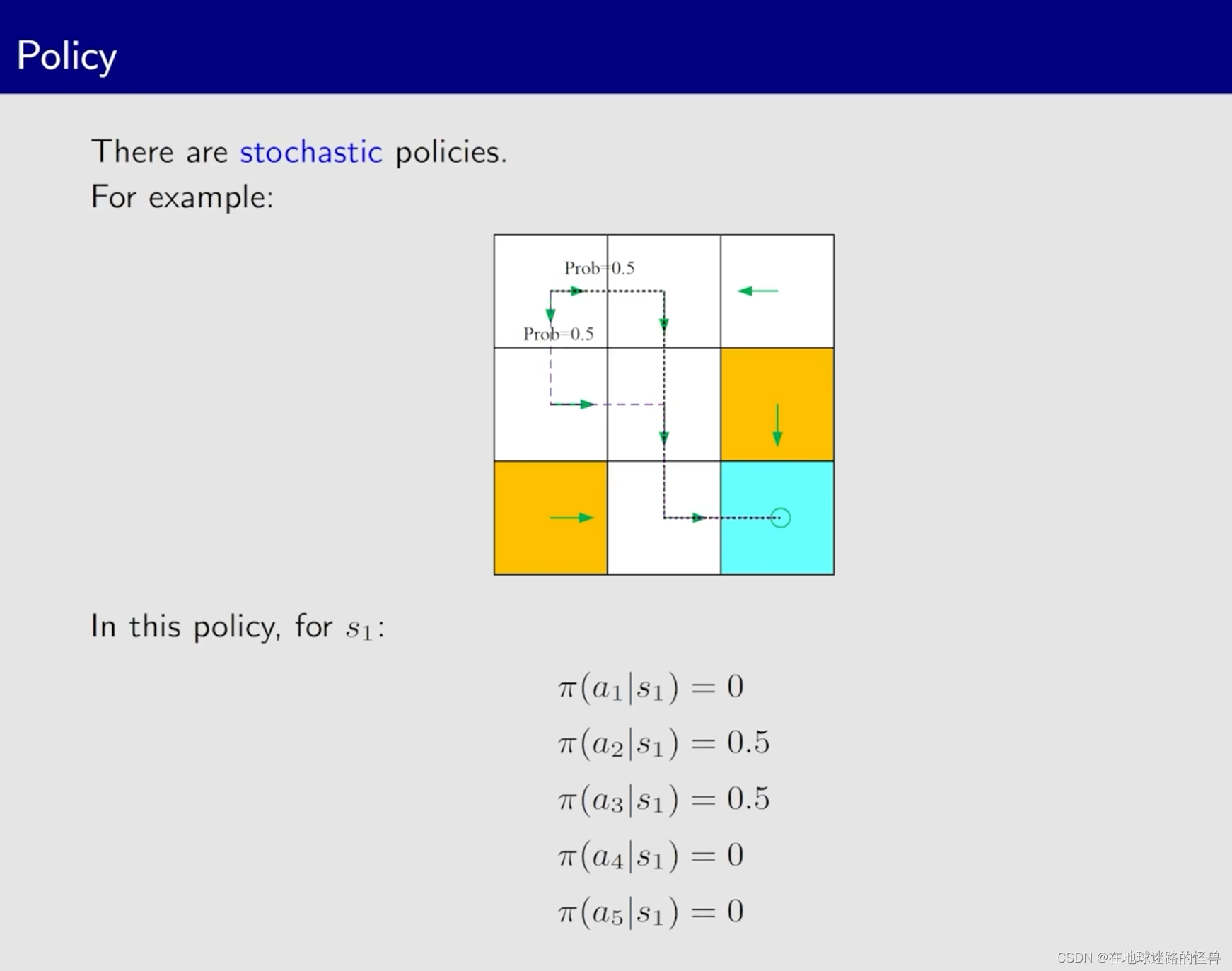
对于上图，我们使用的是 箭头 来抽象的表示了一下策略，但在实际当中我们肯定对于稍微复杂一点的情况是没办法使用箭头的，同样需要使用数学语言来描述这个行为。

仍然使用条件概率来进行描述，对上图来说，以第一行式子为例：针对在 s1 的情况下，它的策略 Π （在强化学习中，Π 用来统一表示策略）会采取 a1 行为的策略的概率值为 0。

和状态转移的情况差不多，策略也存在有不确定性的情况，但也可以使用条件概率的方式来进行描述：

表格的展示：

reward

表格展示上面的过程：

同理，对于不确定的状态（比如采取 a1 的 reward 值可能是不确定的），表格依然具有局限性。

因此同样需要使用更加一般化的数学表达的方式，也就是之前提到的条件概率。

注意：reward 取决于当前所选择的 state 和 action，和未来的状态没有关系。

trajectory and return

trajectory 实际上是一个叫 state-action-reward 的这么一个链：

return 则是针对于一个 trajectory 而言的，一个 trajectory 的 return 就是沿着这个 trajectory 所得到的所有的 reward 加起来：

对于不同的 policy ，那么很容易想到对应的 trajectory 就是不一样的：

return 的作用是什么呢？

刚刚分析了两个 trajectory，那么究竟哪个 trajectory 比较好 或者说 哪个 policy 比较好呢？

return 的一个作用则是可以帮我们做出这样的判断：

discounted return

从上图不难看出，如果我们的 agent 走到了网格中的最右下角，也就是进入到了我们的 target-area，它如果在这个位置循环进入的话，那么 return 就会一直+1，这样加下去，最后的 return 一定是个无穷大的值，如果 return 沿着这个无穷长的 trajectory 增加，最后就会发散掉，为了解决这个问题，引入了 discounted rate（折扣率） 的概念：

通过 discounted rate 与 return 的结合，就得到了 discounted return 的概念。

有了这个 discounted return 的概念有什么作用呢？

一个是解决了刚刚的发散问题，从上图可以看到通过高等数学的知识是可以证明对于一个在区间 [0, 1) 当中的值 γ，其计算出来的 discounted return 值是收敛的，是一个有限的值。

另一个作用则是它能够去平衡这种更远未来我所得到的 reward 和更近未来我所能得到的 reward 。

什么意思？

就是当 γ 趋近于 0 的时候，因为γ的三次方后面的四次方、五次方等的次方数是非常高的，所以γ的三四五次方等会很快的衰减掉，这时候最后的 return 值就主要依赖于最开始所得到的 reward。

相反如果 γ 是趋近于 1 的话，那么未来的 reward 就衰减的慢，那么它积累起来的 reward 的值就会比较大一点。

因此，通过控制 γ，我们是能够控制 agent 所学习到的策略的。简单的说，如果减小 γ 的值，会让它变得更加的近视，也就是它会更加的注重最近的一些 reward，而如果 γ 比较大的话，则会让它更加的远视，会更加注重长远的这种 reward。

episode

其实就是相当于“回合”的意思，比如上图中的 agent 从开始走到了最终的位置结束了这一回合，那么就可以说是结束了一个 episode。

一个 episode 通常都是有限步的，这样的任务也被称为 episode tasks。

而有些任务是没有终止状态的，这意味着 agent 和环境会永远交互下去，这样的任务称为 continue tasks：

而 episodic 和 continue task 这二者实际上是可以互相转换的，无非就是修改一下策略而已，因此本课程不严格区分这两类任务，都当作 continue task 进行讲解。

马尔可夫决策过程（MDP）

上面将强化学习过程中的一些基本概念都讲了一遍，接下来将这些概念放到一个称为 MDP 的框架当中进行讲解，也就是使用更加正式的方式进行这些概念的讲解。

一个 MDP 具有很多要素，第一个就是包含很多集合：sets：

第二个 MDP 的要素则是 probability distribution（概率分布），比如 状态转移概率、回报概率：

第三个要素是 policy，比如我在状态 s，我有一个策略，这个策略会告诉我采取某一个 action a 的概率究竟是多少：

最后 MDP 还有一个比较独特的性质，称为 memoryless property（历史无关性）：

以上图中的第一行表达式为例：一开始的状态是 s0，然后采取了一个 a1，然后慢慢走到状态 st 时所采取的动作是 a(t+1) ，那么这个时候跳到下一个状态 s(t+1) 的概率等于什么呢？它等于完全不考虑之前的状态历史，比如 s0，反正只知道现在是在状态 st，然后采取动作 a(t+1) 之后跳到状态 s(t+1)，因此这行表达式的左边概率值完全等于右边的概率值：

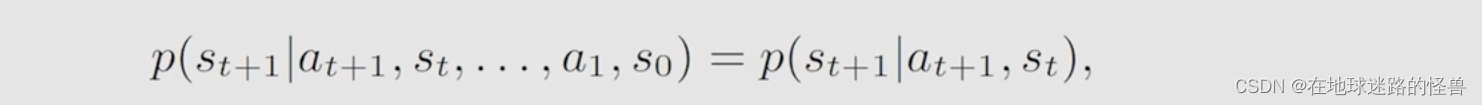
同理，对于所获得的 reward 值也是历史无关的，因此下面这一行表达式的左边概率值也等于右边概率值：

上述这个框架合起来就是 马尔可夫决策过程 框架。

Markov decision process：

Markov：指的就是 Markov 的历史无关性 memoryless property。
decision：指的就是对应的 policy，也就是决定策略。
process：process指的就是从一个状态转移到另一个状态的这种链式的过程，而这个就靠的是前面所提到的各种概念，比如 集合 set、概率分布 probability distribution 等内容来描述。

因此这三个关键词实际上就很好的描述了 MDP 这个框架。

总结

之前说的网格世界的例子，就可以抽象成一个 马尔可夫决策过程：

小结一下本节课的内容：