几何算法——10.欧拉操作
- 1 欧拉操作
- 1.1 欧拉操作的设计思想
- 1.2 欧拉操作的选取
- 1.3 几个典型的欧拉操作
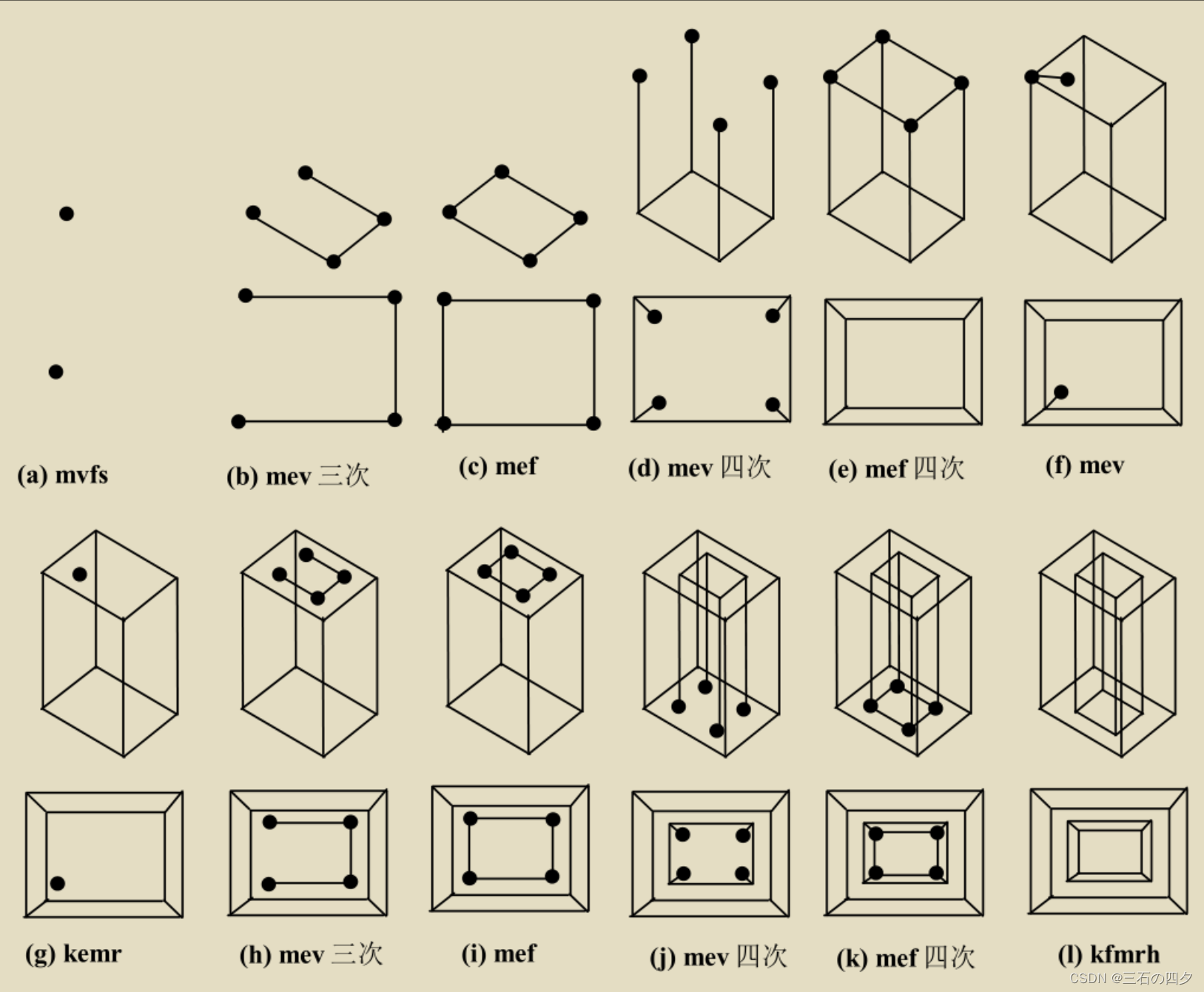
- 1.3.1 mvfs
- 1.3.2 mev
- 1.3.3 mef
- 1.3.4 kemr
- 1.3.5 kfmrh
- 1.4 一个欧拉操作的实例
- 1.5 欧拉操作的三点结论
- 2. 非流形体
- 2.1 非流形模型(non-manifold model)
- 2.2 扩展的欧拉公式
1 欧拉操作
欧拉操作,是由 B.G. Baumgart 于1972年提出,目的是提供有效、正确地建立三维物体复杂的边界数据结构的方法(保证有效性、保证通用性)。
1.1 欧拉操作的设计思想
(1) 提供少数几个公用的边界数据结构生成操作,使得三维物体复杂的边界数据结构可通过这些公用操作逐步构造完成。
(2) 基于欧拉公式保证使用公用数据结构生成操作所生成的边界数据结构具有拓扑有效性。
欧拉公式: v(点数) - e(边数) + f(面数) = 2(s(分离体数) – h(通孔数))+ r(内环数)
1.2 欧拉操作的选取
原则:取具有明显几何意义的基:造点、造边、造环、造面、造体
本文中使用的名称的关键字如下:

For instance, the name “mev” translates as “Make Edge, vertex”.
C.Braid 所取了一组基:
mvfs,mev,mef,kemr,kfmrh
1.3 几个典型的欧拉操作
1.3.1 mvfs
功能:定义一个体、一个面(含一个外环)、一个点。
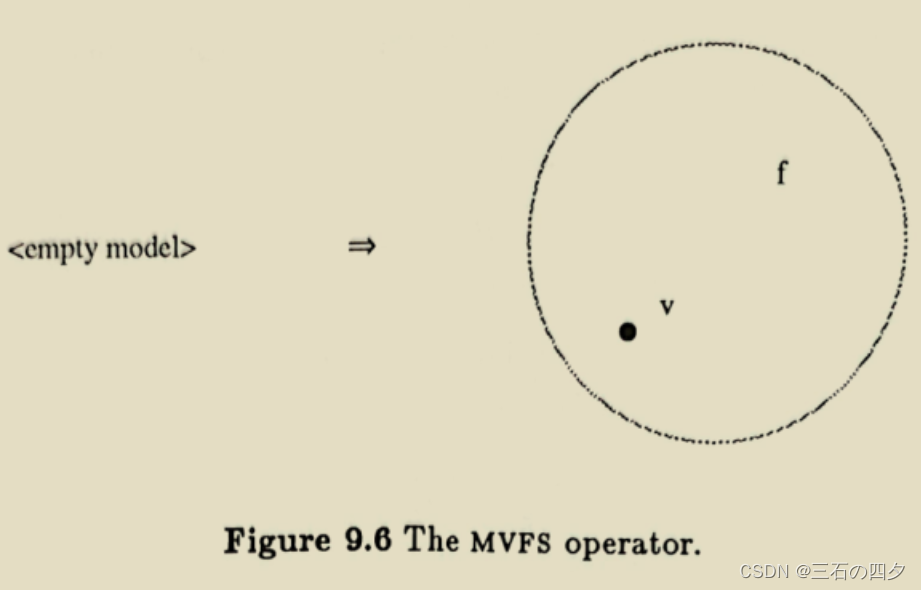
1.3.2 mev
功能:定义一个新点,同时定义一条连接新点与另一给定点的边。
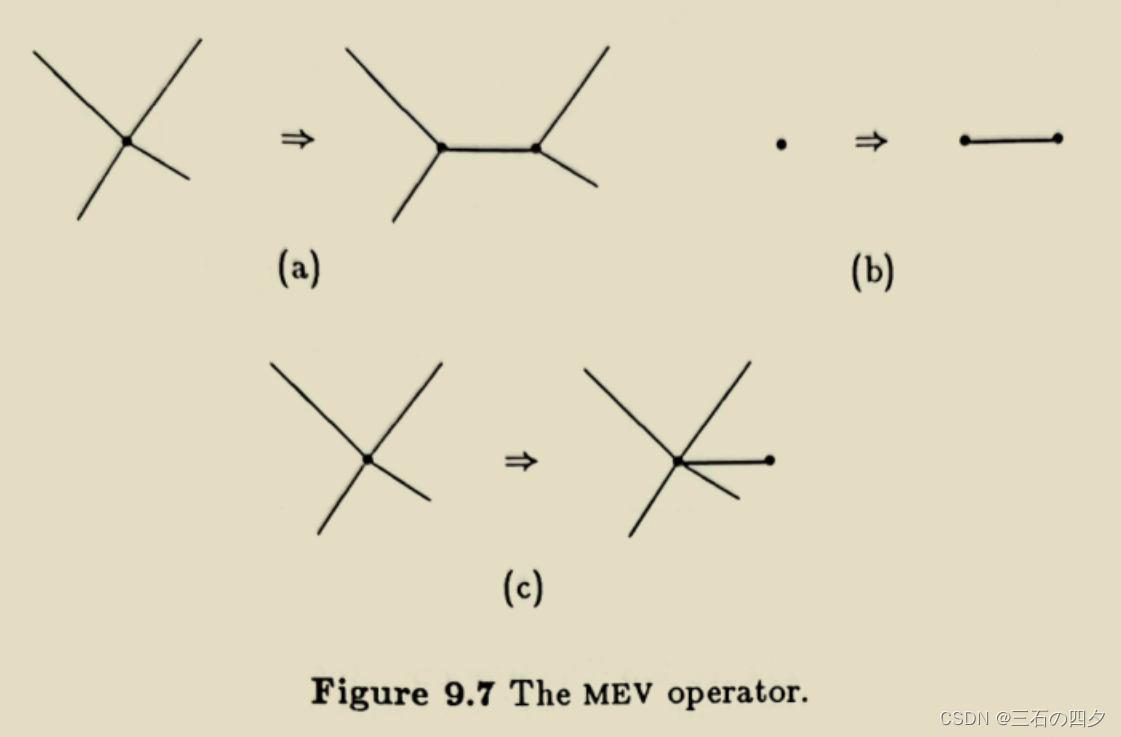
1.3.3 mef
功能:以两给定点为端点定义一条新的边,同时定义一个新的面(含一个新的环)。
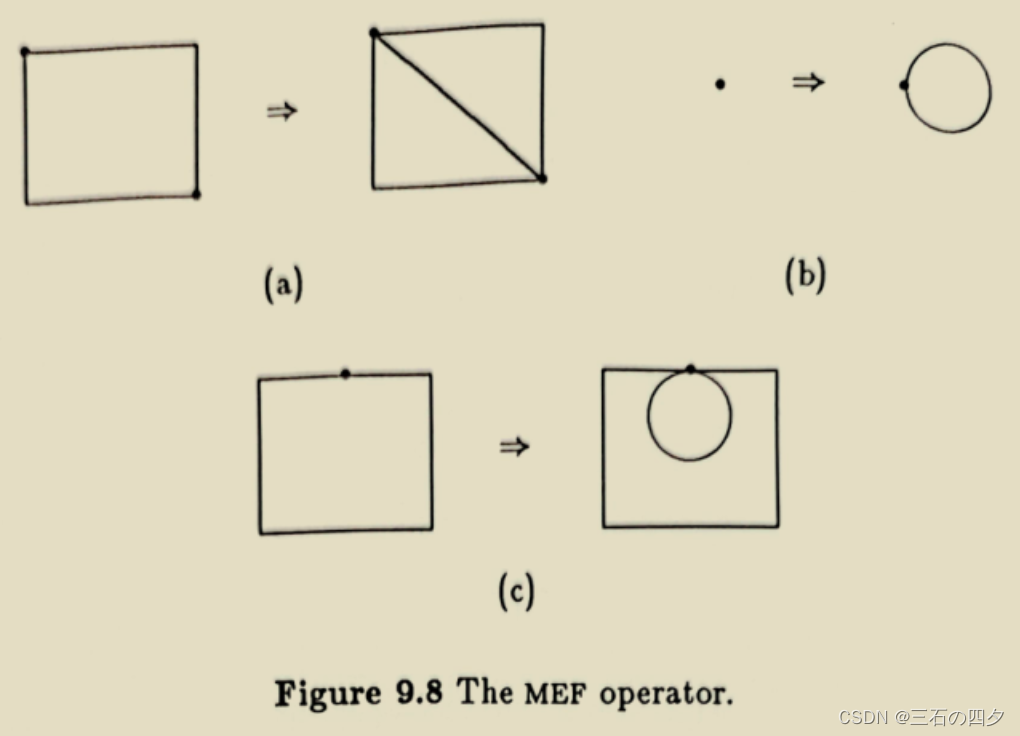
1.3.4 kemr
功能:消去环中的一条边,定义一个内环。
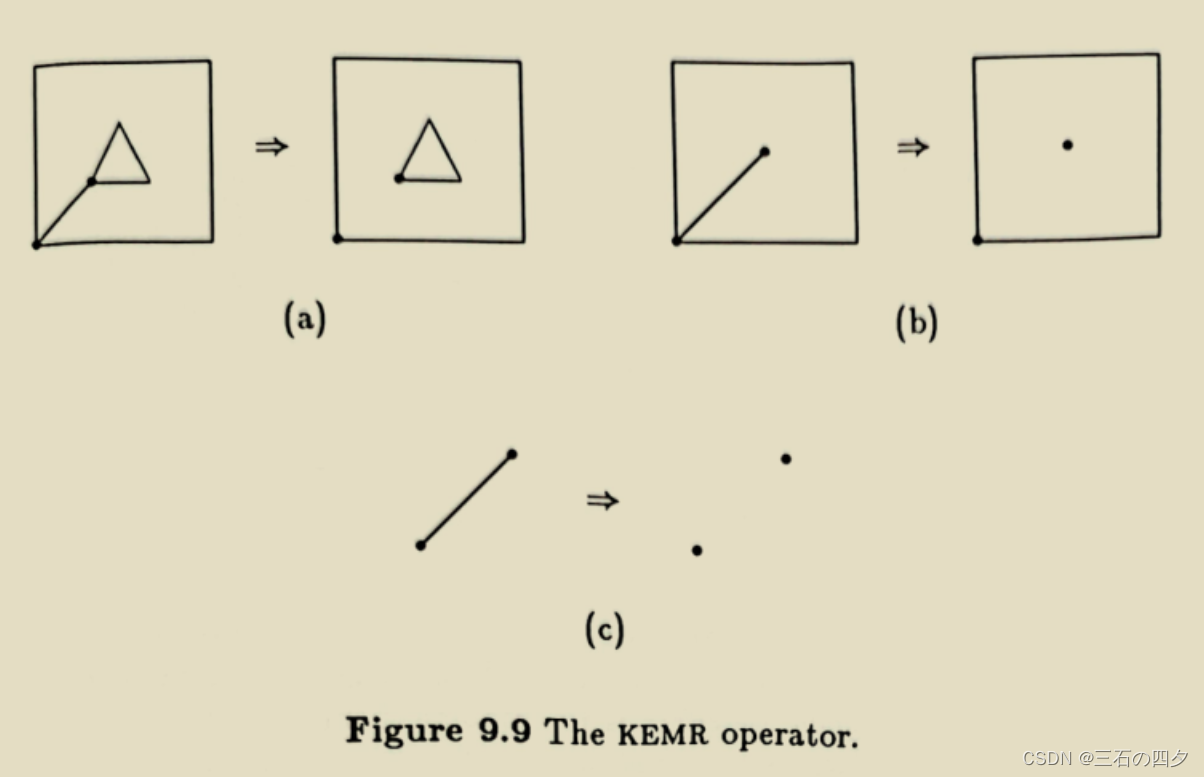
1.3.5 kfmrh
功能:删除一个面,并将其定义为另一个面的内环,进而在体中生成一个通孔或将两物体合并成一个物体。
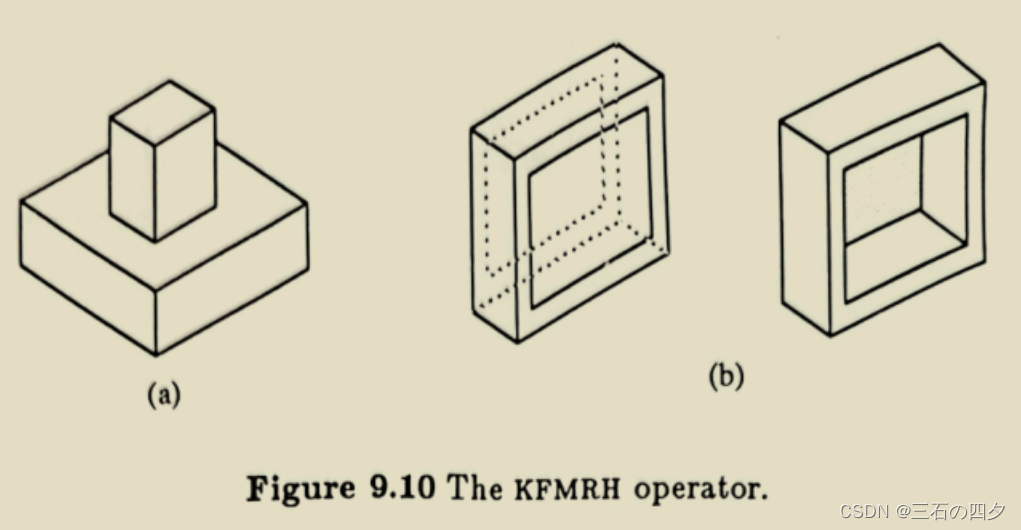
1.4 一个欧拉操作的实例
用欧拉操作构造右侧物体(长方体内带方形通孔)
1.5 欧拉操作的三点结论
Mantyla从理论上得到了以下结果:
(1) 所有流形体的边界表示都可由欧拉操作构造出来;
(2) 由欧拉操作构造出的边界表示在拓扑结构上一定是有效的;
(3) 将这种表示正确地嵌入欧几里德空间结果一定是流形体。
2. 非流形体
2.1 非流形模型(non-manifold model)
非流形体引起集合运算算法上的困难,因此传统的实体造型系统都限定处理正常的情况,即要求形体是正规集,它的边界必须拓扑等价于流形。
实体造型技术从流形转向非流形,一方面有理论研究上的意义,但更重要的是出于工程应用上的实际需要。
2.2 扩展的欧拉公式
V – E + F = 2(S - H) + R
(V - Vr) – (E – Er) + (F - Fr) – I = 2(S - H)
Vr: 与迷向点相连的伞数-1
Fr:内环数
Er: 与迷向边相连的楔数-1
I: 孤立的几何元素的数目





![[Redis] Redis实战](https://img-blog.csdnimg.cn/c7d0ff8db4514906bf8a8259a7bb7360.png)
![[附源码]java毕业设计实践教学管理系统](https://img-blog.csdnimg.cn/353823c997794b1cbfe2e187bcbd3561.png)