Problem: 931. 下降路径最小和
文章目录
- 题目描述
- 思路
- 复杂度
- Code
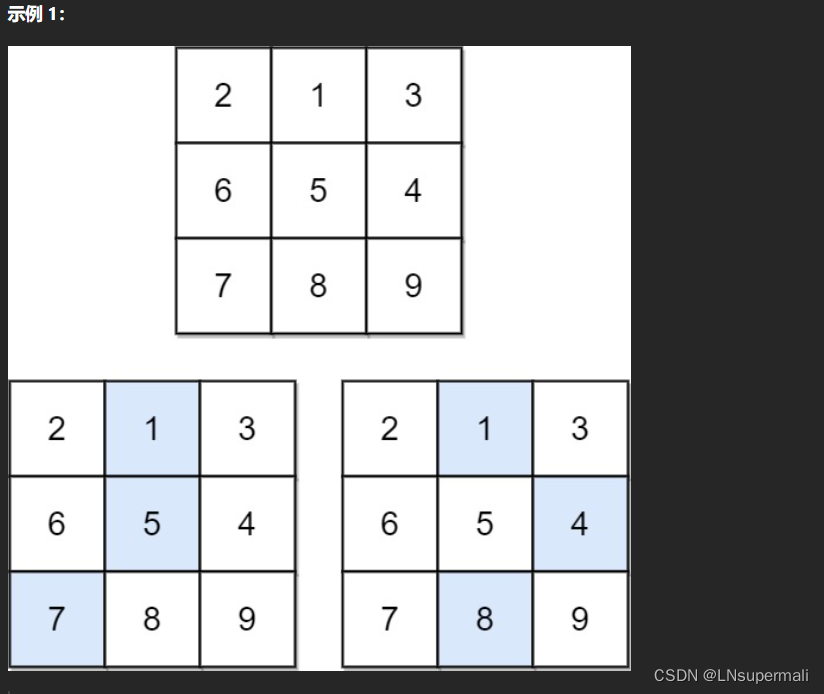
题目描述
思路
1.定义状态:我们定义dp[i][j]为从矩阵的第一行到达位置(i, j)的最小下降路径和。
2.初始化状态:对于矩阵的第一行,即i = 0时,dp[0][j]就是矩阵的第一行的元素值,即matrix[0][j]。
3.状态转移:对于i > 0,dp[i][j]可以从dp[i - 1][j - 1],dp[i - 1][j]或dp[i - 1][j + 1]转移得到,转移时需要加上当前位置的元素值matrix[i][j],并取这三个值的最小值。
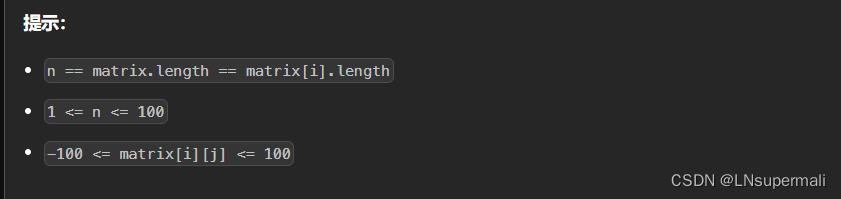
4.边界处理:在进行状态转移时,需要注意矩阵的边界。如果j - 1,j或j + 1超出了矩阵的列数范围,我们可以将其视为一个非常大的值,例如99999,这样在取最小值时就不会被选中。
5.使用备忘录:由于存在重叠子问题,我们可以使用一个备忘录来避免重复计算。在计算dp[i][j]之前,我们首先查看备忘录中是否已经计算过该值,如果已经计算过,我们就直接返回备忘录中的值,否则再进行计算,并将计算结果存入备忘录中。
6.求解答案:最后,我们遍历矩阵的最后一行,找出最小的下降路径和,即为答案。
希望这个思路对你有所帮助!如果你还有其他问题,欢迎随时向我提问。我很乐意帮助你!
复杂度
时间复杂度:
O ( n 2 ) O(n^2) O(n2);其中 n n n为数组的大小
空间复杂度:
O ( n 2 ) O(n^2) O(n2)
Code
class Solution {
vector<vector<int>> memo;
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int n = matrix.size();
int res = INT_MAX;
// Initialize memo with a large value
memo = vector<vector<int>>(n, vector<int>(n, 66666));
// The end point could be any column in matrix[n-1]
for (int j = 0; j < n; ++j) {
res = std::min(res, dp(matrix, n - 1, j));
}
return res;
}
int dp(vector<vector<int>>& matrix, int i, int j) {
// Check index validity
if (i < 0 || j < 0 || i >= matrix.size() || j >= matrix[0].size()) {
return 999999;
}
//Base case
if (i == 0) {
return matrix[0][j];
}
// Check memo to avoid repeated calculation
if (memo[i][j] != 66666) {
return memo[i][j];
}
// State transition
memo[i][j] = matrix[i][j] + min({dp(matrix, i - 1, j), dp(matrix, i - 1, j - 1), dp(matrix, i - 1, j + 1)});
return memo[i][j];
}
int min(vector<int> nums) {
return *min_element(nums.begin(), nums.end());
}
};

![ESP8266[ 关于-巴发云MQTT/TCP:arduino 设置回调函数 ] 日志2024/6/29](https://img-blog.csdnimg.cn/direct/4063fa090ada4e83813a7252f0e9d027.png)





![[C++][设计模式][备忘录模式]详细讲解](https://img-blog.csdnimg.cn/direct/8b380a9587904a08a6a749765c07af34.png)