一、研究背景和意义

类风湿关节炎（RA）是一种慢性炎症性疾病，主要影响关节，但也可能影响身体的其他部分。RA的病因尚不完全清楚，但已知其涉及免疫系统的异常反应。患者的免疫系统错误地攻击自身的关节组织，导致炎症、疼痛和关节损伤。RA的长期影响可能包括关节变形、功能丧失和生活质量的显著下降。此外，RA还与心血管疾病等全身性并发症密切相关。在RA的管理和治疗中，早期诊断和干预至关重要。尽管已有多种治疗方法（如药物治疗和物理治疗）用于缓解症状和延缓疾病进展，
但许多患者仍可能经历疾病的急性发作（failure）和血管闭塞（occlusion）。这些急性事件不仅影响患者的健康和生活质量，还增加了医疗负担和社会成本。

二、研究意义

提高早期诊断和预测能力：通过构建预测模型，本研究能够识别出RA患者在未来可能经历急性发作或血管闭塞的高风险个体，从而实现早期干预和个性化治疗。这不仅有助于提高患者的生活质量，还能有效降低医疗成本。

为临床决策提供支持：本研究的预测模型可作为临床医生的辅助工具，帮助他们在治疗决策过程中考虑更多的变量和因素，从而制定更为科学和有效的治疗方案。

推动RA研究的发展：通过深入分析多种生理和病理指标与RA急性事件之间的关系，本研究为RA的病理机制研究提供了新的视角和数据支持，有助于揭示RA的复杂病理机制，推动相关基础研究的发展。

三、实证分析

读取数据集

数据和代码

import pandas as pd

# 加载数据
file_path = 'interpolation_RA_baseline_anytime_failure.csv'
data = pd.read_csv(file_path)
data.head()

查看数据基本信息 

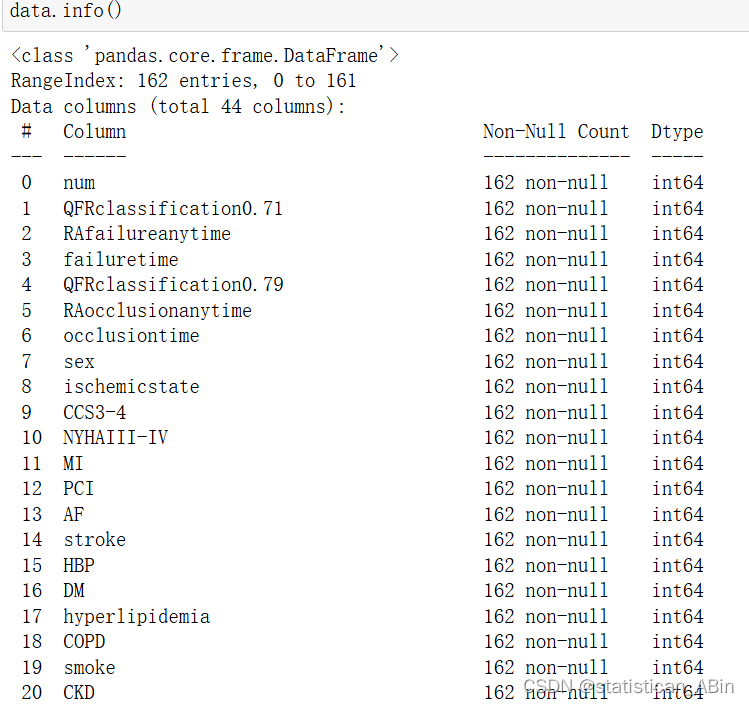
检查缺失值

可以发现没有缺失值

接下来检查检查重复值

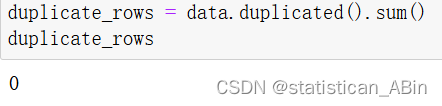
接下来进行描述性统计分析

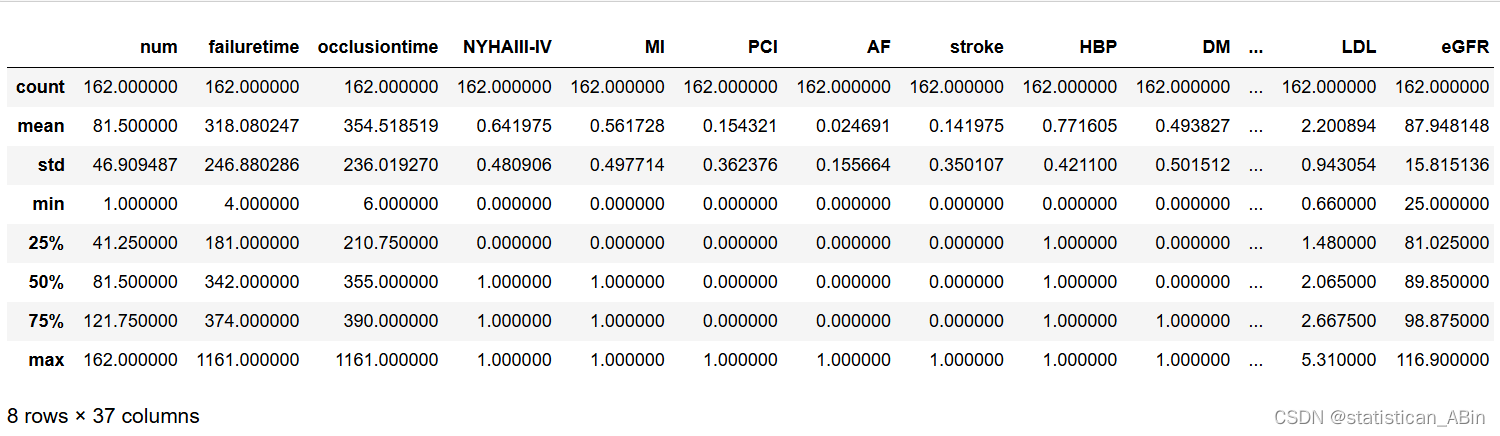
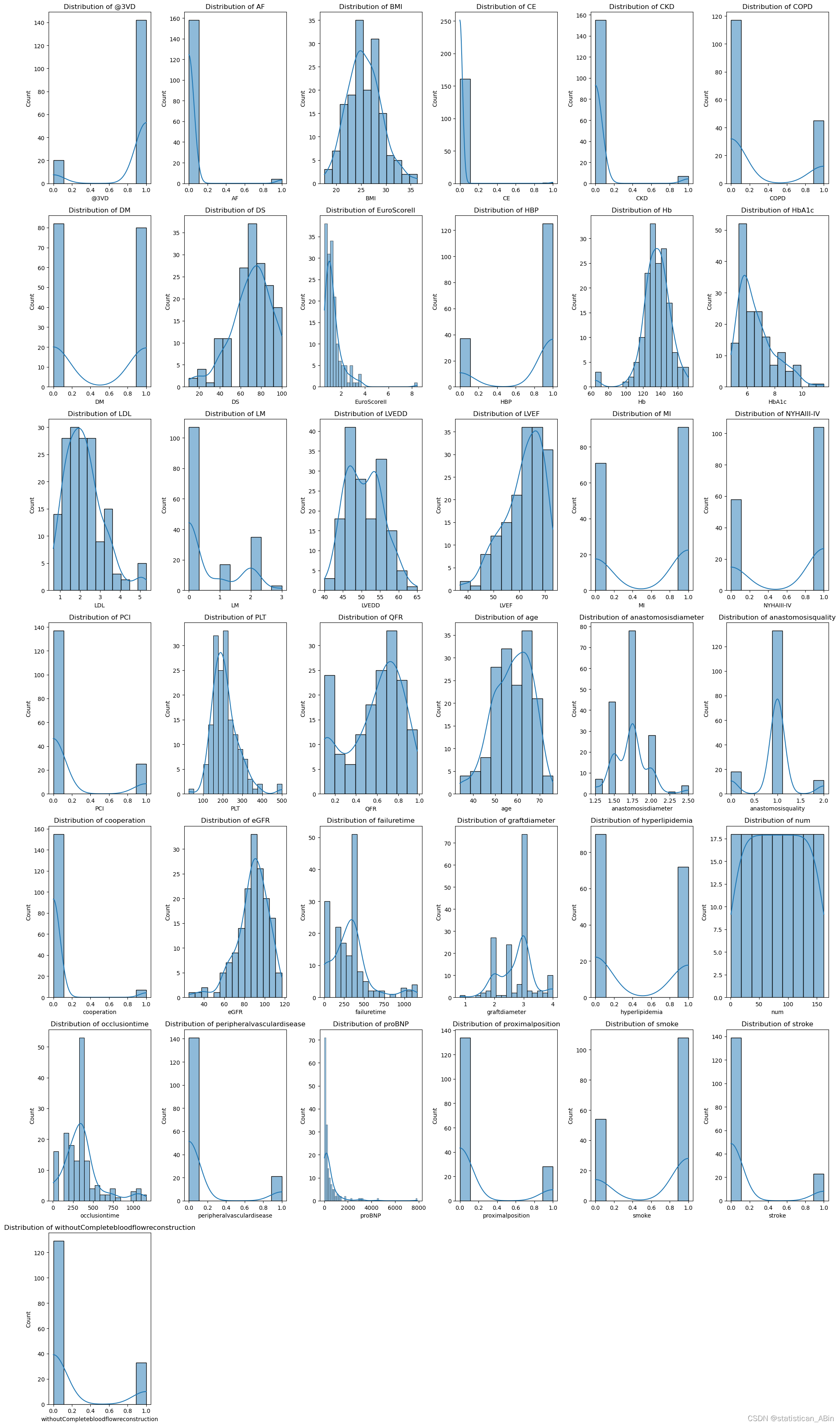
接下来绘制每个特征的直方图

# 绘制分布图，每行6个图
num_plots = len(numerical_columns)
fig, axes = plt.subplots(num_plots // 6 + 1, 6, figsize=(20, 5 * (num_plots // 6 + 1)))

for i, column in enumerate(numerical_columns):
    row, col = divmod(i, 6)
    sns.histplot(data[column].dropna(), kde=True, ax=axes[row, col])
    axes[row, col].set_title(f'Distribution of {column}')

# 删除多余的子图
for j in range(i + 1, len(axes.flatten())):
    fig.delaxes(axes.flatten()[j])

plt.tight_layout()
plt.show()

 

计算相关矩阵

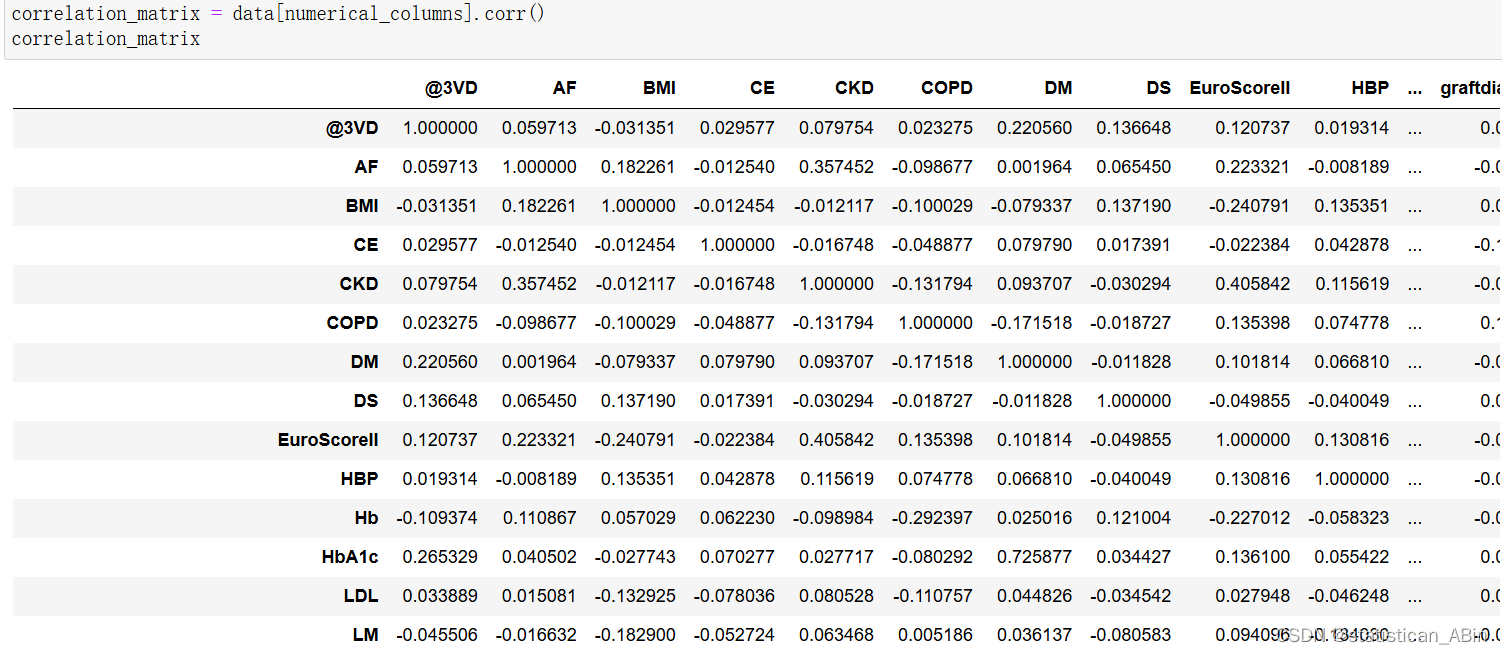也可以绘制热力图

plt.figure(figsize=(12, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

 接下来进行回归分析
线性回归和逻辑回归

# 线性回归
X = data[numerical_columns_with_target]
y = data['RAfailureanytime']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

linear_model = LinearRegression()
linear_model.fit(X_train, y_train)
linear_predictions = linear_model.predict(X_test)

# 逻辑回归
logistic_model = LogisticRegression(max_iter=1000)
logistic_model.fit(X_train, y_train)
logistic_predictions = logistic_model.predict(X_test)

 

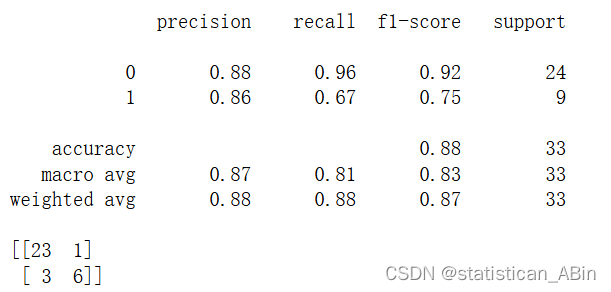
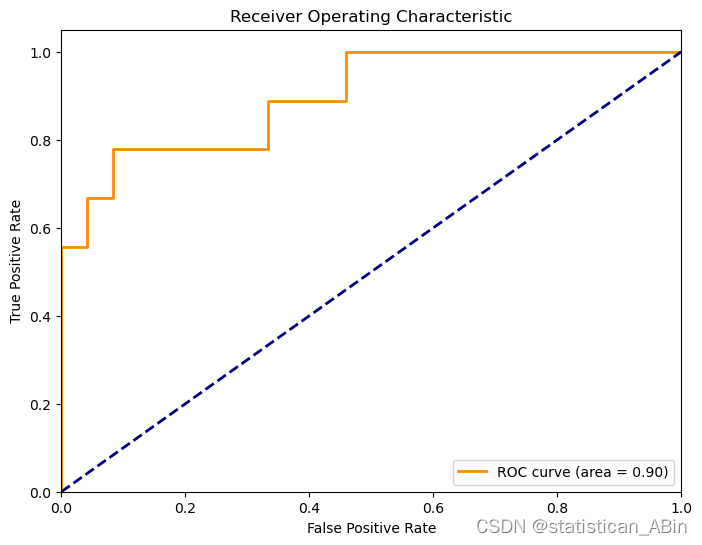
还可以使用其他模型

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC

# 决策树
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, y_train)
dt_predictions = decision_tree.predict(X_test)

# 随机森林
random_forest = RandomForestClassifier()
random_forest.fit(X_train, y_train)
rf_predictions = random_forest.predict(X_test)

# 支持向量机
svc_model = SVC(probability=True)
svc_model.fit(X_train, y_train)
svc_predictions = svc_model.predict(X_test)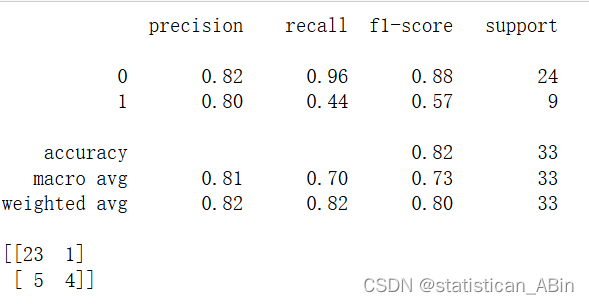

 

接下来进行生存分析
生存曲线和Cox回归模型

# Cox回归模型
cox_model = CoxPHFitter()
cox_model.fit(data, duration_col='failuretime', event_col='RAfailureanytime')
cox_model.print_summary()

 

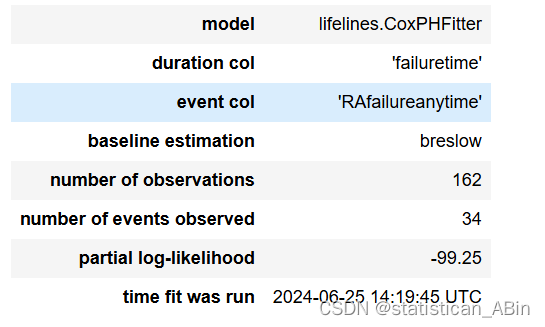
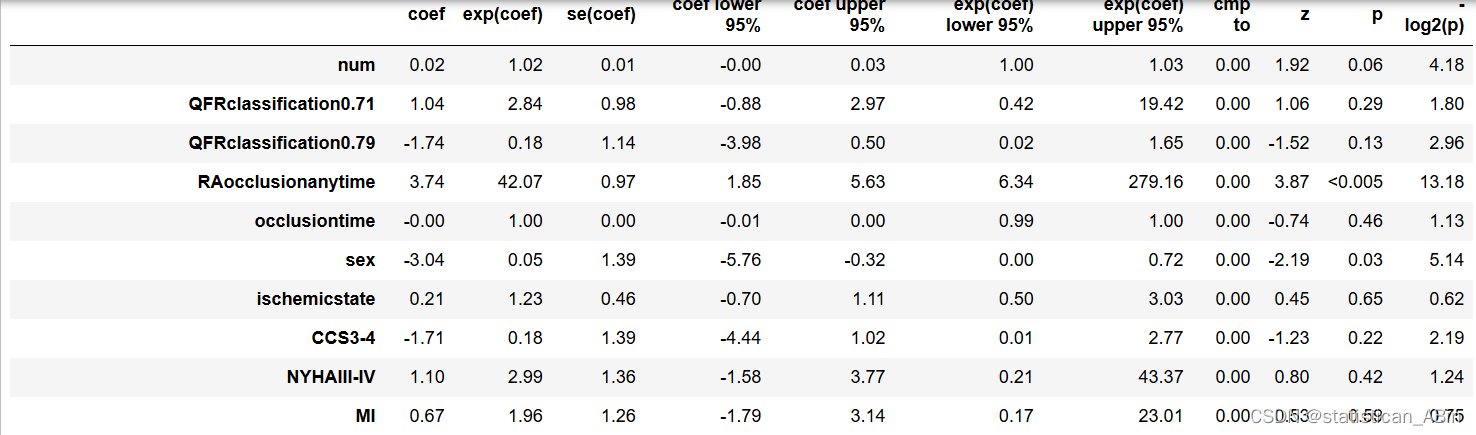
四、结论

本研究通过分析一组包含多种临床和生理指标的RA患者数据，构建了线性回归和逻辑回归模型，用于预测RA患者的急性发作和血管闭塞情况。

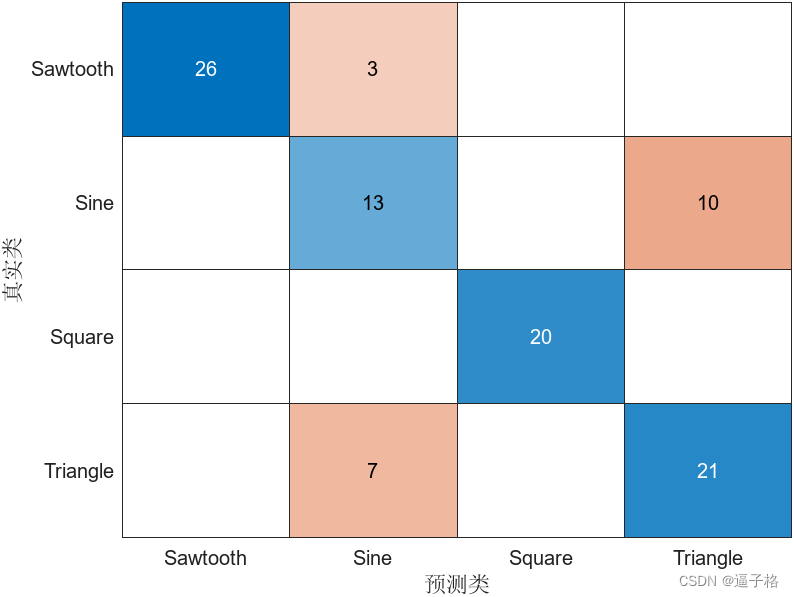
研究结果显示，模型在分类和预测方面表现出较高的准确性和可靠性。具体来说，逻辑回归模型的整体准确率为88%，在精确度、召回率和F1评分等方面均表现良好。ROC曲线的AUC值表明模型具有较高的分类性能，能够有效区分高风险和低风险患者。通过本研究的成果，临床医生可以更早地识别出高风险患者，从而采取早期干预措施，减少急性事件的发生率。此外，本研究还为进一步的RA病理机制研究提供了数据支持，推动了RA研究的发展。

未来，随着数据量的增加和模型的不断优化，预测模型的准确性和应用范围将进一步提升。我们希望本研究的成果能够在实际临床中得到应用，为RA患者的管理和治疗带来实质性的改善。同时，我们也期待更多的研究者参与到这一领域，共同探索和解决RA这一复杂疾病带来的挑战。