目录

1. Input Embedding

2. Positional Encoding

3. Multi-Head Attention

4. Add & Norm

5. Feedforward + Add & Norm

6.代码展示

（1）layer_norm

（2）encoder_layer=1

---

最近刚好梳理了下transformer，今天就来讲讲它~

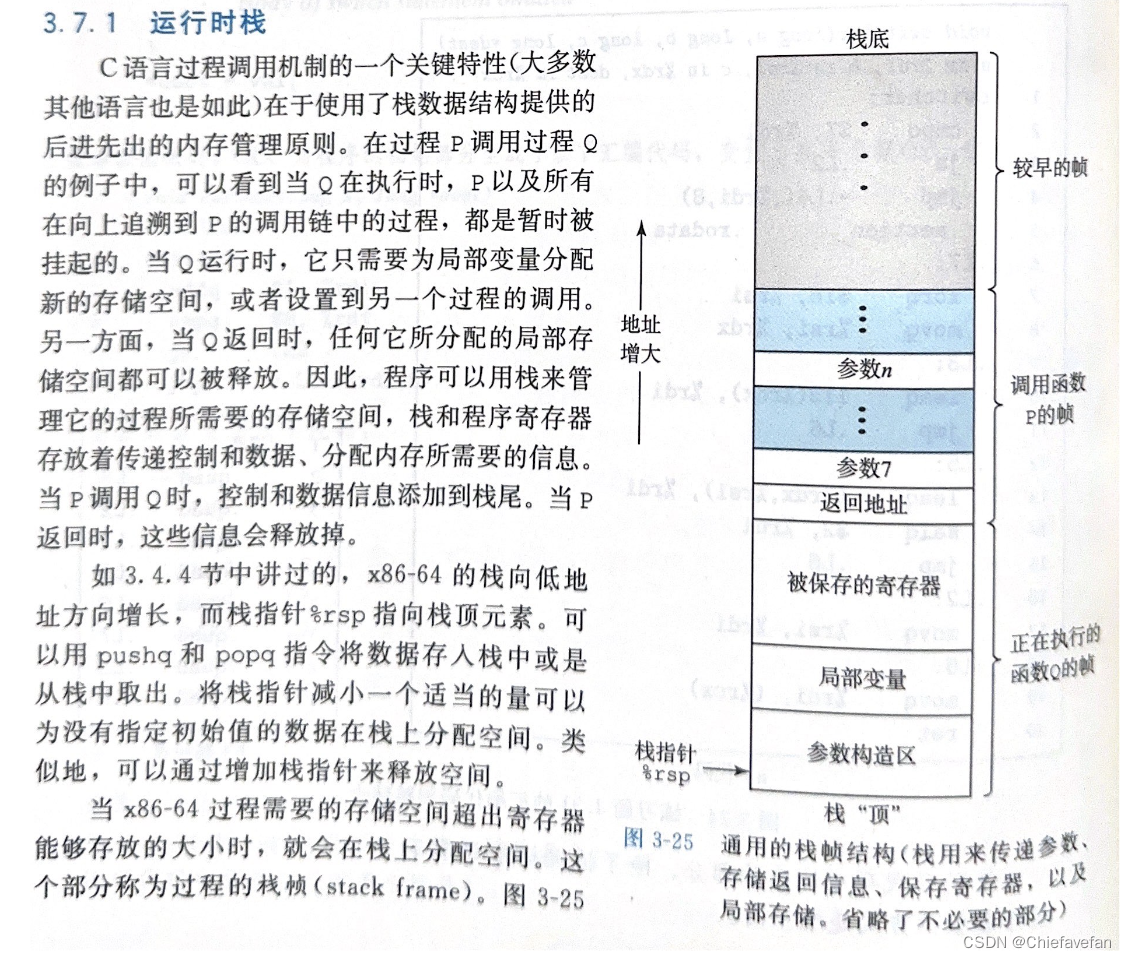
        Transformer是谷歌大脑2017年在论文attention is all you need中提出来的seq2seq模型，它的本质就是由编码器和解码器组成，今天的主角则是其中的编码器（在BERT预训练模型中也只用到了编码器部分）如下图所示，这个模块的输入为 𝑋 （每一行代表一个句子，batchsize有多大就有多少行），我们将从输入到隐藏层按照从1到4的顺序逐层来看一下各个维度的变化。

1. Input Embedding

        所谓的Embedding其实就是查字典或者叫查表，也就是将一个句子里的每一个字转化为一个维度为embedding dimension的向量来表示，因此 𝑋 经过嵌入后变成 𝑋𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔 ，三个维度分别表示一个批次的句子数，每个句子的字数，每个字的嵌入维度。

2. Positional Encoding

        位置编码，按照字面意思理解就是给输入的位置做个标记，简单理解比如你就给一个字在句子中的位置编码1，2，3，4这样下去，高级点的比如作者用的正余弦函数

𝑃𝐸(𝑝𝑜𝑠,2𝑖)=𝑠𝑖𝑛(𝑝𝑜𝑠/100002𝑖/𝑑𝑚𝑜𝑑𝑒𝑙)

𝑃𝐸(𝑝𝑜𝑠,2𝑖+1)=𝑐𝑜𝑠(𝑝𝑜𝑠/100002𝑖/𝑑𝑚𝑜𝑑𝑒𝑙)

 

        其中pos表示字在句子中的位置，i指的词向量的维度。经过位置编码，相当于能够得到一个和输入维度完全一致的编码数组 𝑋𝑝𝑜𝑠 ，当它叠加到原来的词嵌入上得到新的词嵌入

𝑋𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔=𝑋𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔+𝑋𝑝𝑜𝑠

        此时的维度为：一个批次的句子数 × 一个句子的词数 × 一个词的嵌入维度

3. Multi-Head Attention

        注意力机制，其实可以理解为就是在计算相关性，很自然的想法就是去更多地关注那些相关更大的东西。这里首先要引入Query，Key和Value的概念，Query就是查询的意思，Key就是键用来和你要查询的Query做比较，比较得到一个分数（相关性或者相似度）再乘以Value这个值得到最终的结果。

        那么这个Q，K，V从哪里来呢，这里采用的是self-attention的方式，也就是从输入自己 𝑋𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔 来产生，即做线性映射产生Q，K，V：

𝑄=𝑋𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔∗𝑊𝑄𝐾=𝑋𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔∗𝑊𝐾𝑉=𝑋𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔∗𝑊𝑉

        这里三个权重矩阵均为维度为Embedding的方阵，也就是说Q，K，V的维度和 𝑋𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔 是一致的。

        接下来考虑什么叫做multi-head（多头）呢，本质上就是从embedding的维度上将矩阵切分为多份，每一份就是一个头，比如之前的Q，K，V切完后的维度就是一个批次的句子数 × 一个句子的词数 × 头数 × (词嵌入维度/头数)这个多头的切分体现在最后两个维度：词嵌入维度=数 × (词嵌入维度/头数)为了便于计算，通常会将第二第三维度进行转置，即最终的维度为一个批次的句子数 × 头数 × 一个句子的词数 × (词嵌入维度/头数)

        接下来说说注意力机制的计算，假设Q，K，V为切分完后的矩阵（其中一个头），根据两个向量的点积越大越相似，我们通过 𝑄𝐾𝑇 求出注意力矩阵，再根据注意力矩阵来给Value进行加权，即

𝐴𝑡𝑡𝑒𝑛𝑡𝑖𝑜𝑛(𝑄,𝐾,𝑉)=𝑠𝑜𝑓𝑡𝑚𝑎𝑥(𝑄𝐾𝑇𝑑𝑘)𝑉

        其中 𝑑𝑘 是为了把注意力矩阵变成标准正态分布，softmax进行归一化，使每个字与其他字的注意力权重之和为1。这一操作使得每一个字的嵌入都包含当前句子内所有字的信息，注意Attention(Q,K,V)的维度和 𝑉 的维度保持一致。

4. Add & Norm

这里主要做了两个操作

• 一个是残差连接（或者叫做短路连接），说得直白点就是把上一层的输入 𝑋 和上一层的输出加起来 𝑆𝑢𝑏𝐿𝑎𝑦𝑒𝑟(𝑋) ，即 𝑋+𝑆𝑢𝑏𝐿𝑎𝑦𝑒𝑟(𝑋) ，举例说明，比如在注意力机制前后的残差连接：

𝑋𝑒𝑚𝑏𝑒𝑑𝑑𝑖𝑛𝑔+𝐴𝑡𝑡𝑒𝑛𝑡𝑖𝑜𝑛(𝑄,𝐾,𝑉)

• 一个是LayerNormalization（作用是把神经网络中隐藏层归一为标准正态分布，加速收敛），具体操作是将每一行的每一个元素减去这行的均值, 再除以这行的标准差, 从而得到归一化后的数值。

5. Feedforward + Add & Norm

前馈网络也就是简单的两层线性映射再经过激活函数一下，比如

𝑋ℎ𝑖𝑑𝑑𝑒𝑛=𝑅𝑒𝑙𝑢(𝑋ℎ𝑖𝑑𝑑𝑒𝑛∗𝑊1∗𝑊2)

残差操作和层归一化同步骤3.

---

上述的1，2，3，4就构成Transformer中的一个encoder模块，经过1，2，3，4后得到的就是encode后的隐藏层表示，可以发现它的维度其实和输入是一致的！即：一个批次中句子数 × 一个句子的字数 × 字嵌入的维度

6.代码展示

（1）layer_norm

bs=2,seq=3,dim=5

import torch

batch_size = 2
seq = 3
fea_dim = 5
X = torch.rand(batch_size,seq,fea_dim)
layer_norm = torch.nn.LayerNorm(fea_dim)
out = layer_norm(X)
print(out)
print('-'*30)

mean = torch.mean(X,dim=-1,keepdim=True)
std = torch.sqrt(torch.var(X,unbiased=False,dim=-1,keepdim=True) + 1e-5)
weight = layer_norm.state_dict()['weight']
bias = layer_norm.state_dict()['bias']
my_norm = ((X - mean)/std) * weight + bias
print(my_norm)

（2）encoder_layer=1

bs=1,seq=1,dim=6,head=1

import torch

seq = 1
dim = 6
heads = 1
batch_size = 1
value = torch.rand(batch_size,seq,dim)

encoder_layer = torch.nn.TransformerEncoderLayer(dim,heads,dropout=0.0,batch_first=True)
out = encoder_layer(value)
print(out)

# 多头自注意力
def my_scaled_dot_product(query,key,value):
    qk_T = torch.mm(query,key.T)
    qk_T_scale = qk_T / torch.sqrt(torch.tensor(value.shape[1]))
    qk_exp = torch.exp(qk_T_scale)
    qk_exp_sum = torch.sum(qk_exp,dim=1,keepdim=True)
    qk_softmax = qk_exp / qk_exp_sum
    v_attn = torch.mm(qk_softmax,value)
    return v_attn,qk_softmax

in_proj_weight = encoder_layer.state_dict()['self_attn.in_proj_weight']
in_proj_bias = encoder_layer.state_dict()['self_attn.in_proj_bias']

out_proj_weight = encoder_layer.state_dict()['self_attn.out_proj.weight']
out_proj_bias = encoder_layer.state_dict()['self_attn.out_proj.bias']

batch_V_output = torch.empty(batch_size,seq,dim)
for i in range(batch_size):
    in_proj = torch.mm(value[i],in_proj_weight.T) + in_proj_bias
    Qs,Ks,Vs = torch.split(in_proj,dim,dim=-1)
    head_Vs = []
    attn_weight = torch.zeros(seq,seq)
    for Q,K,V in zip(torch.split(Qs,dim//heads,dim=-1),torch.split(Ks,dim//heads,dim=-1),torch.split(Vs,dim//heads,dim=-1)):
        head_v,_ = my_scaled_dot_product(Q,K,V)
        head_Vs.append(head_v)
    V_cat = torch.cat(head_Vs,dim=-1)
    V_ouput = torch.mm(V_cat,out_proj_weight.T) + out_proj_bias
    batch_V_output[i] = V_ouput

# 第一次加
first_Add = value + batch_V_output

# 第一次layer_norm
norm1_mean = torch.mean(first_Add,dim=-1,keepdim=True)
norm1_std = torch.sqrt(torch.var(first_Add,unbiased=False,dim=-1,keepdim=True) + 1e-5)
norm1_weight = encoder_layer.state_dict()['norm1.weight']
norm1_bias = encoder_layer.state_dict()['norm1.bias']
norm1 = ((first_Add - norm1_mean)/norm1_std) * norm1_weight + norm1_bias

# feed forward
linear1_weight = encoder_layer.state_dict()['linear1.weight']
linear1_bias = encoder_layer.state_dict()['linear1.bias']
linear2_weight = encoder_layer.state_dict()['linear2.weight']
linear2_bias = encoder_layer.state_dict()['linear2.bias']
linear1 = torch.matmul(norm1,linear1_weight.T) + linear1_bias
linear1_relu = torch.nn.functional.relu(linear1)
linear2 = torch.matmul(linear1_relu,linear2_weight.T) + linear2_bias

# 第二次加
second_Add = norm1 + linear2

# 第二次layer_norm
norm2_mean = torch.mean(second_Add,dim=-1,keepdim=True)
norm2_std = torch.sqrt(torch.var(second_Add,unbiased=False,dim=-1,keepdim=True) + 1e-5)
norm2_weight = encoder_layer.state_dict()['norm2.weight']
norm2_bias = encoder_layer.state_dict()['norm2.bias']
norm2 = ((second_Add - norm2_mean)/norm2_std) * norm2_weight + norm2_bias
print(norm2)