LeetCode：经典题之2、445 题解及延伸

news2025/1/21 15:41:01

系列目录

88.合并两个有序数组
52.螺旋数组
567.字符串的排列
643.子数组最大平均数
150.逆波兰表达式
61.旋转链表
160.相交链表
83.删除排序链表中的重复元素
389.找不同
1491.去掉最低工资和最高工资后的工资平均值
896.单调序列
206.反转链表
92.反转链表II
141.环形链表
142.环型链表
21.合并两个有序列表
24.两辆交换链表中的节点
876.链表的中间节点
143. 重排链表
2.两数相加
445.两数相加II

目录

  • 系列目录
  • 2. 两数相加
  • 445. 两数相加 II
    • 栈
      • 调用STL库
      • 数组模拟栈
      • 链表模拟栈
    • 运行时栈(Runtime Stack)[^1]

2. 两数相加

🌟链表

原题链接


C++
若未特殊标明，以下题解均写用C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        // 定义一个 tail 让其移动
        // 这里head 充当一个 💂
        ListNode *head = nullptr, *tail = nullptr;
        int carry = 0;
        // l1 或 l2 存在 
        while (l1 || l2 || carry) {
            // 这里不能写成——要进行一个 数据类型的转化
            // int sum = carry + l1->val + l2->val;
            int n1 = l1 ? l1->val : 0;
            int n2 = l2 ? l2->val : 0;
            int sum = carry + n1 + n2;
            // head 不存在，初始化新链表
            if (!head) {
                // 小数点向前挪一位，只取个位，进位(十位)通过 carry记录
                head = tail = new ListNode(sum % 10);
            } else {
                tail->next = new ListNode(sum % 10);
                // 记得更新 tail
                tail = tail->next;
            }

            // 取整得到 carry 进位位 
            carry = sum / 10;

            if (l1) l1 = l1->next;
            if (l2) l2 = l2->next;
        }

    //	// l1 和 l2 都遍历完了 还有多余的进位
    //  if (carry > 0)
    //      tail->next = new ListNode(carry);
    // 这两行可以并在while中

        return head;
    }
};





445. 两数相加 II

🌟 (反转)链表+递归+栈

原题链接


思路
有了上一题的启发，我们可以先将逆序相加的两个链表，反转过来相加，再反转回去并返回


C++
若未特殊标明，以下题解均写用C++

方法一 反转链表+递归  

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
// class类 默认 private
//private:
    ListNode* reverseList(ListNode* head) {
        // pre-preserve	cur-current nxt-next        
        ListNode *pre = nullptr, *cur = head;
        while (cur) {
            ListNode *nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }

        return pre;
    }

    ListNode *addTwo(ListNode* l1, ListNode* l2) {
        ListNode *head = nullptr, *tail = nullptr;
        int carry = 0;
        while (l1 || l2) {
            int n1 = l1 ? l1->val : 0;
            int n2 = l2 ? l2->val : 0;
            int sum = carry + n1 + n2;
            
            // 初始化新链表
            if (!head) {    
                head = tail = new ListNode(sum % 10);
            } else {
                tail->next = new ListNode(sum % 10);
                tail = tail->next;
            }
			
            // 更新进位位
            carry = sum / 10;
            
            // 别忘了更新 l1、l2
            if (l1) l1 = l1->next;
            if (l2) l2 = l2->next;
        }
        
        // 溢出的进位位处理
        if (carry > 0)
            tail->next = new ListNode(carry);

        return head;
    }

public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1 = reverseList(l1);
        l2 = reverseList(l2);
        auto l3 = addTwo(l1, l2);

        // 将l1 和 l2 反转过来相加；再将所得的结果反转回去
        return reverseList(l3);
    }
};


写法二

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
private:
    ListNode* reverseList(ListNode* head) {
        // pre-preserve	cur-current nxt-next 
        ListNode *pre = nullptr, *cur = head;
        while (cur) {
            ListNode *nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }

        return pre;
    }

    ListNode* addTwo(ListNode* l1, ListNode* l2) {
        int carry = 0;
        ListNode *tail = nullptr, *head = nullptr;
        while (l1 || l2 || carry) {
            int n1 = l1 ? l1->val : 0;
            int n2 = l2 ? l2->val : 0;
            int sum = n1 + n2 + carry;
            
            if (!head) {
                head = tail = new ListNode(sum % 10);
            } else {
                tail->next = new ListNode(sum % 10);
                // 别忘了更新 tail
                tail = tail->next;
            }

            carry = sum / 10;
            
            if (l1) l1 = l1->next;
            if (l2) l2 = l2->next;
        } // while_end

        return head;
    }

public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1 = reverseList(l1);
        l2 = reverseList(l2);
        
        auto l3 = addTwo(l1, l2);

        return reverseList(l3);
    }
};




思路：
借助栈逆序处理所有数位

方法二 栈

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        stack<int> s1, s2;
        while (l1) {
            s1.push(l1->val);
            l1 = l1->next;
        }

        while (l2) {
            s2.push(l2->val);
            l2 = l2->next;
        }

        int carry = 0;
        // 用于 反转链表
        ListNode *res = nullptr;
        while (!s1.empty() or !s2.empty() or carry) {
            int a = s1.empty() ? 0 : s1.top();
            int b = s2.empty() ? 0 : s2.top();
            
            // 逻辑删除栈顶元素
            if (!s1.empty()) s1.pop();
            if (!s2.empty()) s2.pop();

            int sum = a + b + carry;
            carry = sum / 10;
            sum %= 10;

            // 可用 auto 代替 ListNode*
            auto node = new ListNode(sum);

            // 反转链表 
            node->next = res;
            res = node;
        }

        return res;
    }
};

栈

  • 遵循后进先出(LIFO, Last In First Out)的原则
  • 主要用于存储数据元素，这些数据元素被称为栈项(Stack Items)

基本操作

  1. Push(推入)：将一个新元素添加到栈的顶部
  2. Pop(弹出)：从栈的顶部移除一个元素，并返回该元素的值 如果栈为空，则弹出操作可能会失败或引发错误
  3. Top(顶部)：返回栈顶元素的值，但不移除它
  4. IsEmpty(是否为空)：检查栈是否为空
  5. Size(大小)：返回栈中元素的数量

实现

在C++中，通常使用标准模板库(STL)中的stack容器来实现栈
或用数组或链表来模拟栈

应用

栈在计算机科学中有广泛的应用，包括函数调用(调用栈)、表达式求值(如后缀表达式)、括号匹配、深度优先搜索(DFS)等 在操作系统中，栈也用于保存局部变量和返回地址 在C++中，当函数被调用时，其参数和局部变量通常被存储在调用栈上


调用STL库

调用STL库

#include <iostream>  
#include <stack>  
  
using namespace std;

int main() {  
	stack<int> myStack; // 创建一个空的int类型栈  
  
    // Push元素到栈中  
    myStack.push(1);  
    myStack.push(2);  
    myStack.push(3);  
  
    // 显示栈顶元素  
    cout << "栈顶元素: " << myStack.top() << endl; // 输出: 3  
  
    // 弹出并显示栈顶元素  
    cout << "弹出的元素: " << myStack.pop() << endl; // 输出: 3  
  
    // 显示栈的大小  
    cout << "栈的大小: " << myStack.size() << endl; // 输出: 2  
  
    // 检查栈是否为空  
    if (myStack.empty()) {  
        cout << "栈为空" << endl;  
    } else {  
        cout << "栈不为空" << endl; // 输出: 栈不为空  
    }  
  
    return 0;  
}




数组模拟栈

数组模拟

#include <iostream>  
#include <cassert>

using namespace std; 
  
class Stack {  
private:  
    int* arr;
    int peek;  
    int capacity;  
  
public:  
    // 构造函数  
    Stack(int size) {  
        capacity = size;  
        arr = new int[capacity];  
        peek = -1; // 栈顶初始化为-1，表示栈为空  
    }  
  
    // 析构函数
    // 释放 new 运算符分配的资源，对象的生命周期结束后自动被调用
    ~Stack() {  
        delete[] arr;  
    }  
  
    // 检查栈是否为空  
    bool isEmpty() {  
        return peek == -1;  
    }  
  
    // 检查栈是否已满  
    bool isFull() {  
        return peek == capacity - 1;  
    }  
  
    // 入栈操作  
    void push(int value) {  
        if (isFull()) {  
            cerr << "Stack is full, cannot push element.\n";  
            return;  
        }  
        arr[peek ++] = value; // 先移动栈顶指针，再赋值  
    }  
  
    // 出栈操作  
    int pop() {  
        if (isEmpty()) {  
            cerr << "Stack is empty, cannot pop element.\n";  
            return -1; // 或者可以抛出异常  
        }  
        return arr[peek --]; // 先返回栈顶元素的值，再移动栈顶指针  
    }  
  
    // 查看栈顶元素  
    int top() {  
        if (isEmpty()) {  
            cerr << "Stack is empty, cannot top element.\n";  
            return -1; // 或者可以抛出异常  
        }  
        return arr[peek];  
    }  
  
    // 获取栈的大小  
    int size() {  
        return peek + 1;  
    }  
};  
  
int main() {  
    Stack s(5); // 创建一个容量为5的栈  
  
    s.push(1);  
    s.push(2);  
    s.push(3);  
  
    cout << "peek element: " << s.top() << endl; // 输出: 3  
    cout << "Stack size: " << s.size() << endl;  // 输出: 3  
  
    cout << "Popped element: " << s.pop() << endl; // 输出: 3  
  
    return 0;  
}




链表模拟栈

链表模拟

#include <iostream>  
  
using namespace std;

// 链表节点类  
template <typename T>  
class ListNode {  
public:  
    T data;  
    ListNode* next;  
  
    ListNode(T x) : data(x), next(nullptr) {}  
};  
  
// 栈类  
template <typename T>  
class Stack {  
private:  
    ListNode<T>* top; // 栈顶指针  
  
public:  
    Stack() : top(nullptr) {} // 构造函数  
  
    // 判断栈是否为空  
    bool isEmpty() const {  
        return top == nullptr;  
    }  
  
    // 向栈顶添加元素  
    void push(T x) {  
        ListNode<T>* newNode = new ListNode<T>(x);  
        newNode->next = top;  
        top = newNode;  
    }  
  
    // 从栈顶移除元素  
    T pop() {  
        if (isEmpty()) {  
            throw runtime_error("Stack is empty!");  
        }  
        ListNode<T>* temp = top;  
        T data = temp->data;  
        top = top->next;  
        delete temp;  
        return data;  
    }  
  
    // 返回栈顶元素但不移除  
    T topElement() const {  
        if (isEmpty()) {  
            throw runtime_error("Stack is empty!");  
        }  
        return top->data;  
    }  
  
    // 析构函数，释放所有节点  
    ~Stack() {  
        while (!isEmpty()) {  
            pop();  
        }  
    }  
};  
  
int main() {  
    Stack<int> s;  
    s.push(1);  
    s.push(2);  
    s.push(3);  
  
    cout << "Top element: " << s.topElement() << endl;  
  
    s.pop();  
    cout << "Top element after pop: " << s.topElement() << endl;  
  
    return 0;  
}




运行时栈(Runtime Stack)1

程序在执行过程中用于存储函数调用的相关信息和局部变量等数据的内存区域

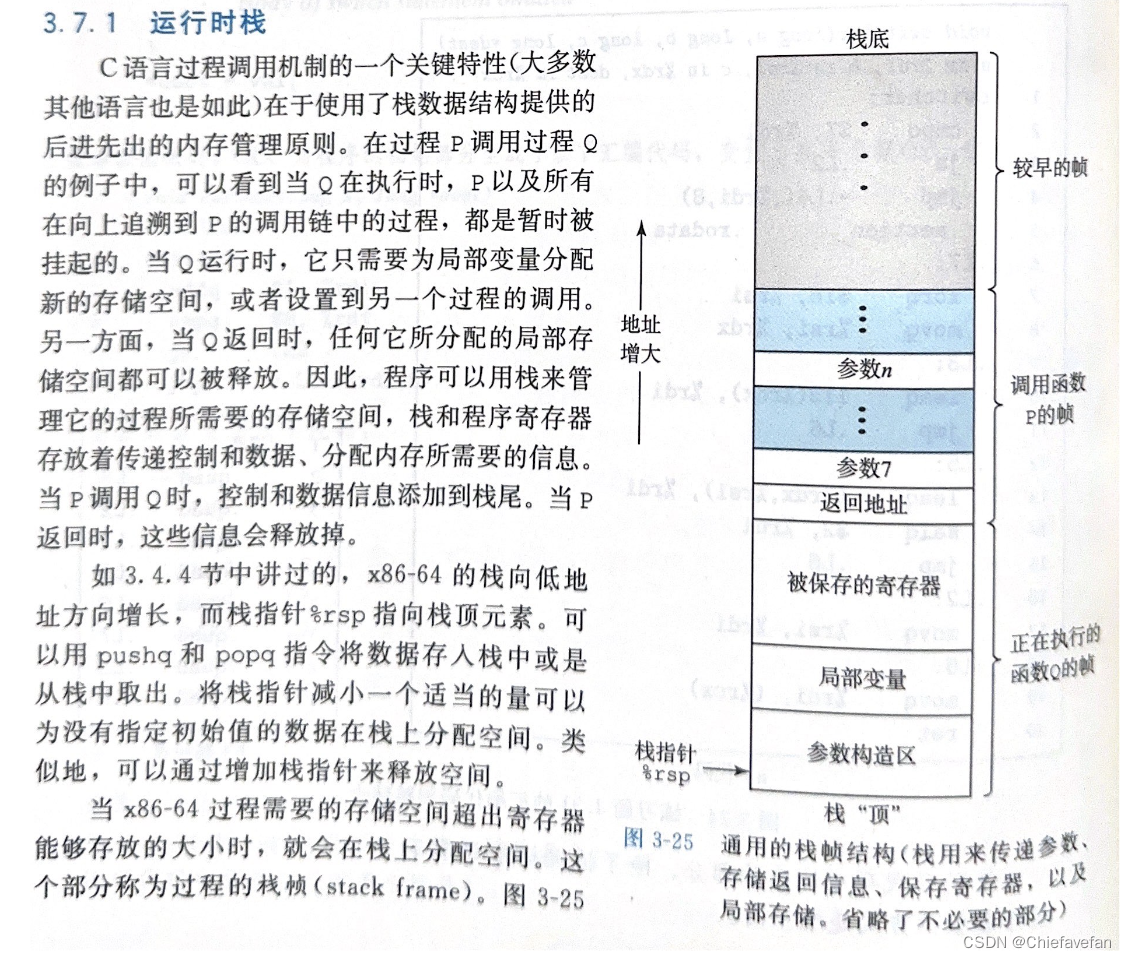
请添加图片描述

  1. 栈的基本结构和功能
  • 栈的结构：栈是一种后进先出(LIFO)的数据结构，程序栈实际上是一块内存区域，满足先进后出的原则 从栈底到栈顶，地址由高变低，所以新加入栈的以及新开辟的空间的地址都是较小的
  • 功能：运行时栈主要用来支持函数调用的执行
    这包括保存函数的返回地址、传递函数参数、存储局部变量等
  1. 栈帧(Stack Frame)
  • 定义：栈帧是为单个过程(函数)分配的那一小部分栈
    它保存了函数调用的上下文信息
  • 内容：
    • 局部变量：包括函数内部定义的变量，以及作为参数传递的变量
    • 返回地址：当函数执行完毕后，需要返回到调用该函数的地方继续执行，这个地址就被保存在栈帧中
    • 其他信息：可能还包括一些其他的状态信息，如保存的寄存器值等
  1. 运行时栈的操作
  • 分配空间：当函数调用发生时，会为其在栈上分配一个新的栈帧，用于存储该函数的局部变量等信息
  • 释放空间：当函数执行完毕并返回时，其栈帧会被销毁，释放之前分配的空间 这个过程是通过栈指针%rsp的移动来实现的
  1. 寄存器与栈的关系
  • 帧指针(Frame Pointer)：%rbp：基指针寄存器(Base Pointer Register)，保存当前栈帧开始的位置 大多数信息访问都是相对于帧指针进行的
  • 栈指针(Stack Pointer)：%rsp：栈指针寄存器(Stack Pointer Register)，始终指向栈顶 通过减小栈指针的值来分配空间，增加栈指针来释放空间
  1. 运行时栈与程序执行
  • 函数调用：当函数被调用时，会将其参数、局部变量等信息压入栈中，并保存返回地址
    并跳转到被调用函数的起始地址执行
  • 函数返回：当函数执行完毕时，会弹出栈顶的返回地址，并跳转到该地址继续执行
    同时，该函数的栈帧也会被销毁，释放其占用的空间
  1. 栈的大小限制
  • 运行时栈的大小是有限的，如果递归调用过深或局部变量过多，可能导致栈溢出(Stack Overflow)
  1. 总结

运行时栈是程序执行过程中非常重要的内存区域，它支持函数调用的执行，并通过栈帧来保存函数调用的上下文信息

  1. 参考自 《深入理解计算机系统》CSAPP ↩︎

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1880452.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

github主页这样优化，让人眼前一亮

github主页这样优化，让人眼前一亮

我的主页&#xff08;一之十六&#xff09; 1. 创建与账户ID同名的仓库 注意&#xff1a;记得勾选Add a README file 2. markdown语法自定义README.md 3. 辅助工具 优秀profile&#xff1a;https://zzetao.github.io/awesome-github-profile/动态文字&#xff1a;https://r…
阅读更多...
pytest测试框架pytest-cov插件生成代码覆盖率

pytest测试框架pytest-cov插件生成代码覆盖率

Pytest提供了丰富的插件来扩展其功能&#xff0c;本章介绍下pytest-cov插件&#xff0c;用于生成测试覆盖率报告&#xff0c;帮助开发者了解哪些部分的代码被测试覆盖&#xff0c;哪些部分还需要进一步的测试。 pytest-cov 支持多种报告格式&#xff0c;包括纯文本、HTML、XML …
阅读更多...
修复vcruntime140.dll方法分享

修复vcruntime140.dll方法分享

修复vcruntime140.dll方法分享 最近在破解typora的时候出现了缺失vcruntime140.dll文件的报错导致软件启动失败。所以找了一番资料发现都不是很方便的处理&#xff0c;甚至有的dll处理工具还需要花钱&#xff1f;&#xff1f;&#xff1f;&#xff1f;&#xff0c;我本来就是为…
阅读更多...
前端学习 Vue 插槽如何实现组件内容分发？

前端学习 Vue 插槽如何实现组件内容分发？

目录 一、Vue.js框架介绍二、什么是Vue 插槽三、Vue 插槽的应用场景四、Vue 插槽如何实现组件内容分发 一、Vue.js框架介绍 Vue.js是一个用于构建用户界面的渐进式JavaScript框架。它设计得非常灵活&#xff0c;可以轻松地被集成到现有的项目中&#xff0c;也可以作为一个完整…
阅读更多...
新型发电系统——光伏行业推动能源转型

新型发电系统——光伏行业推动能源转型

一、发展背景 “十四五”期间&#xff0c;随着“双碳”目标提出及逐步落实&#xff0c;本就呈现出较好发展势头的分布式光伏发展有望大幅提速。就“十四五”光伏发展规划&#xff0c;国家发改委能源研究所可再生能源发展中心副主任陶冶表示&#xff0c;“双碳”目标意味着国家…
阅读更多...
轻松解锁电脑强悍性能，4000MHz的玖合星舞 DDR4 内存很能打

轻松解锁电脑强悍性能，4000MHz的玖合星舞 DDR4 内存很能打

轻松解锁电脑强悍性能&#xff0c;4000MHz的玖合星舞 DDR4 内存很能打 哈喽小伙伴们好&#xff0c;我是Stark-C~ 很多有经验的电脑玩家在自己DIY电脑选购内存条的时候&#xff0c;除了内存总容量&#xff0c;最看重的参数那就是频率了。内存频率和我们常说的CPU主频一样&…
阅读更多...
计网之IP

计网之IP

IP IP基本认识 不使用NAT时&#xff0c;源IP地址和目的IP地址不变&#xff0c;只要源MAC和目的MAC地址在变化 IP地址 D类是组播地址&#xff0c;E类是保留地址 无分类地址CIDR 解决直接分类的B类65536太多&#xff0c;C类256太少a.b.c.d/x的前x位属于网路号&#xff0c;剩…
阅读更多...
pytest测试框架pytest-random-order插件随机执行用例顺序

pytest测试框架pytest-random-order插件随机执行用例顺序

Pytest提供了丰富的插件来扩展其功能&#xff0c;本章介绍下pytest-random-order插件&#xff0c;随机设置pytest测试用例的运行顺序&#xff0c;并对随机性进行一些控制。 官方文档&#xff1a; https://pytest-cov.readthedocs.io/en/latest/index.html 适配版本说明&#x…
阅读更多...
ComfyUI局部重绘的四种方式 （附件工作流在最后）

ComfyUI局部重绘的四种方式 （附件工作流在最后）

前言 局部重绘需要在图片中选择重绘区域&#xff0c;点击图片右击选择Open in MaskEditor&#xff08;在蒙版编辑器中打开&#xff09;&#xff0c;用鼠标描绘出需要重绘的区域 方式一&#xff1a;重绘编码器 这种方式重绘比较生硬&#xff0c;需要额外搭配使用才行 方式二&…
阅读更多...
ThreadPoolExecutor基于ctl变量的声明周期管理

ThreadPoolExecutor基于ctl变量的声明周期管理

个人博客 ThreadPoolExecutor基于ctl变量的声明周期管理 | iwts’s blog 总集 想要完整了解下ThreadPoolExecutor&#xff1f;可以参考&#xff1a; 基于源码详解ThreadPoolExecutor实现原理 | iwts’s blog ctl字段的应用 线程池内部使用一个变量ctl维护两个值&#xff…
阅读更多...
逆变器--学习笔记（一）

逆变器--学习笔记（一）

并网&#xff1a; 逆变器中的“并网”指的是逆变器将其产生的交流电与电网同步&#xff0c;并输送到公共电网中。并网逆变器通常用于太阳能发电系统和其他分布式发电系统&#xff0c;将其产生的电能输送到电网供其他用户使用。 THD谐波失真总量: 逆变器的THD&#xff08;Tot…
阅读更多...
【TB作品】温度DS18B20读取，温控风扇，ATMEGA128单片机，Proteus仿真

【TB作品】温度DS18B20读取，温控风扇，ATMEGA128单片机，Proteus仿真

读取温度&#xff1b; PWM风扇控制&#xff1b; 蜂鸣器控制。 写博客介绍这个基于ATmega128的作品时&#xff0c;可以从以下几个方面展开描述&#xff1a; 概述 介绍项目的背景和目的&#xff0c;说明使用ATmega128的原因以及项目的整体架构。 硬件设计 主要元件 详细列出…
阅读更多...
180Kg大载重多旋翼无人机技术详解

180Kg大载重多旋翼无人机技术详解

一、机体结构与材料 180Kg大载重多旋翼无人机在机体结构上采用了高强度轻量化设计。其主体框架采用航空铝合金材料&#xff0c;既保证了机体的结构强度&#xff0c;又减轻了整体重量。同时&#xff0c;关键部位如连接件、旋翼支撑臂等则采用碳纤维复合材料&#xff0c;以进一步…
阅读更多...
主流电商平台API接口（天猫获得淘宝商品详情，获得淘宝app商品详情原数据 ，获得淘口令真实url API，按图搜索淘宝商品（拍立淘） API ）

主流电商平台API接口（天猫获得淘宝商品详情，获得淘宝app商品详情原数据 ，获得淘口令真实url API，按图搜索淘宝商品（拍立淘） API ）

主流电商平台商品接口在电商企业中具有重要应用价值。通过商品接口&#xff0c;电商企业可以实现商品同步功能&#xff1a; 商品信息同步&#xff1a;通过接口可以实时同步主流电商平台上的商品信息&#xff0c;包括商品标题、价格、库存、销量等数据&#xff0c;确保企业在自…
阅读更多...
微服务中的Docker详细学习

微服务中的Docker详细学习

Docker的个人理解 首先我对于Docker的理解分为两部分&#xff0c;第一是对名字上的理解&#xff0c;我们都知道docker的英文翻译是“码头工人”的意思&#xff0c;所以我们也可以理解为docker是码头上的一个个集装箱的使用。这也与他的图标很相似。其次我是对于其功能上的理解&…
阅读更多...
Excel显示/隐藏批注按钮为什么是灰色？

Excel显示/隐藏批注按钮为什么是灰色？

在excel中&#xff0c;经常使用批注来加强数据信息的提示&#xff0c;有时候会把很多的批注显示出来&#xff0c;但是再想将它们隐藏起来&#xff0c;全选工作表后&#xff0c;“显示/隐藏批注”按钮是灰色的&#xff0c;不可用。 二、可操作方法 批注在excel、WPS表格中都是按…
阅读更多...
002-基于Sklearn的机器学习入门：回归分析（上）

002-基于Sklearn的机器学习入门：回归分析（上）

本节及后续章节将介绍机器学习中的几种经典回归算法&#xff0c;所选方法都在Sklearn库中聚类模块有具体实现。本节为上篇&#xff0c;将介绍基础的线性回归方法&#xff0c;包括线性回归、逻辑回归、多项式回归和岭回归等。 2.1 回归分析概述 回归&#xff08;Regression&…
阅读更多...
【知识学习】Unity3D中Scriptable Render Pipeline的概念及使用方法示例

【知识学习】Unity3D中Scriptable Render Pipeline的概念及使用方法示例

Unity3D中的Scriptable Render Pipeline&#xff08;SRP&#xff09;是一种高度可定制的渲染管线框架&#xff0c;允许开发者完全控制渲染流程&#xff0c;以适应不同的渲染需求和硬件平台。SRP使得开发者可以编写自己的渲染逻辑&#xff0c;包括摄像机管理、渲染设置、光照处理…
阅读更多...
使用RNN模型构建人名分类器

使用RNN模型构建人名分类器

使用RNN模型构建人名分类器 1 项目需求和实现分析 短文本分类问题 2 数据处理三部曲 场景1&#xff1a;数据处理三部曲示意图 场景2&#xff1a;三个字母onehot编码形状分析 3 构建RNN模型 4 构建训练函数并进行训练 - 有关模型、损失函数、优化器三者在pytorch中的表示 5…
阅读更多...
还不知道工业以太网和现场总线区别???

还不知道工业以太网和现场总线区别???

工业以太网 工业以太网是一种专为工业环境设计的网络通信技术&#xff0c;它基于标准的以太网技术&#xff0c;但针对工业应用进行了优化。工业以太网能够适应高温、低温、防尘等恶劣工业环境&#xff0c;采用TCP/IP协议&#xff0c;与IEEE 802.3标准兼容&#xff0c;并在应用层…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023