基本思想:
回溯法是一种系统地搜索问题解空间的算法,常用于解决组合优化和约束满足问题。其核心思想是利用深度优先搜索逐步构建可能的解,同时在搜索过程中进行剪枝操作,以排除那些无法满足问题约束或不能产生最优解的分支,从而减少不必要的计算,提高搜索效率。
深度优先搜索(DFS)简介:
对于二叉树来说,先序、中序、后序遍历都是深度优先遍历。
深度优先就是一条路径走到底后,再返回上一步,搜索第二条路径。
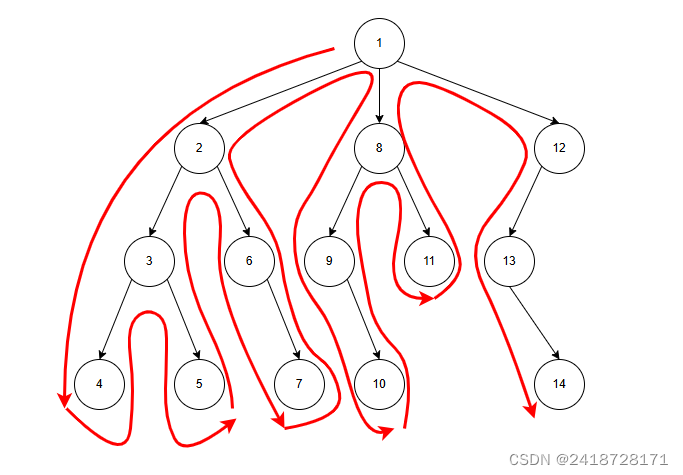
回溯法的一般步骤
1.定义问题并构造状态空间树
明确要解决的问题,确定解空间的结构(通常是一个树或图),确定每一步决策的选择范围。
将问题的解空间表示为一棵树,树的每个节点表示一个状态,根节点表示初始状态,叶节点表示最终状态或解。
2.编写递归函数
编写一个递归函数来遍历状态空间树,函数通常包括以下部分:
- 递归边界:定义何时到达叶节点,即找到一个解或无法继续深入。
- 选择和判断(剪枝):在当前状态下,尝试每一种可能的选择,并判断是否满足约束条件。
- 递归调用:如果满足条件,则进行递归调用,进入下一个状态。
- 回溯:如果不满足条件,或递归调用返回后,需要撤销当前选择,回溯到上一步继续尝试其他选择。
3.输出结果
举例:01背包
问题描述:
有n个物品,它们有各自的体积和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?
背包体积:10
| 物品编号 | 体积(vol) | 价值(val) |
|---|---|---|
| 1 | 8 | 9 |
| 2 | 3 | 2 |
| 3 | 4 | 4 |
| 4 | 3 | 3 |
前面在动态规划中,说了一下蛮力法的如何解决该问题,实际上回溯法与蛮力法差不多,只是搜索方式不同,并添加剪枝(提前结束当前遍历)和回溯(记忆之前的状态)。
1、定义问题并构造状态空间树
前面使用蛮力法解决时,对于问题的每一种状态通过数值的二进制表示,用数字二进制中为1的位置表示该位置的物品是否放入,比如:
1(0000 0001)表示第1个物品放入,其他都不放入;
2(0000 0010)表示第2个物品放入,其他都不放入;
3(0000 0011)表示第1和第2哥物品放入,其他都不放入。
使用回溯法解决问题,需要将问题所有的情况构造成一颗树或图,通过深度优先搜索遍历获取最优解。
每个物品只有两种状态,放入背包或不放入背包,可以将各种物品是否放入构造成一颗二叉树,如下图:
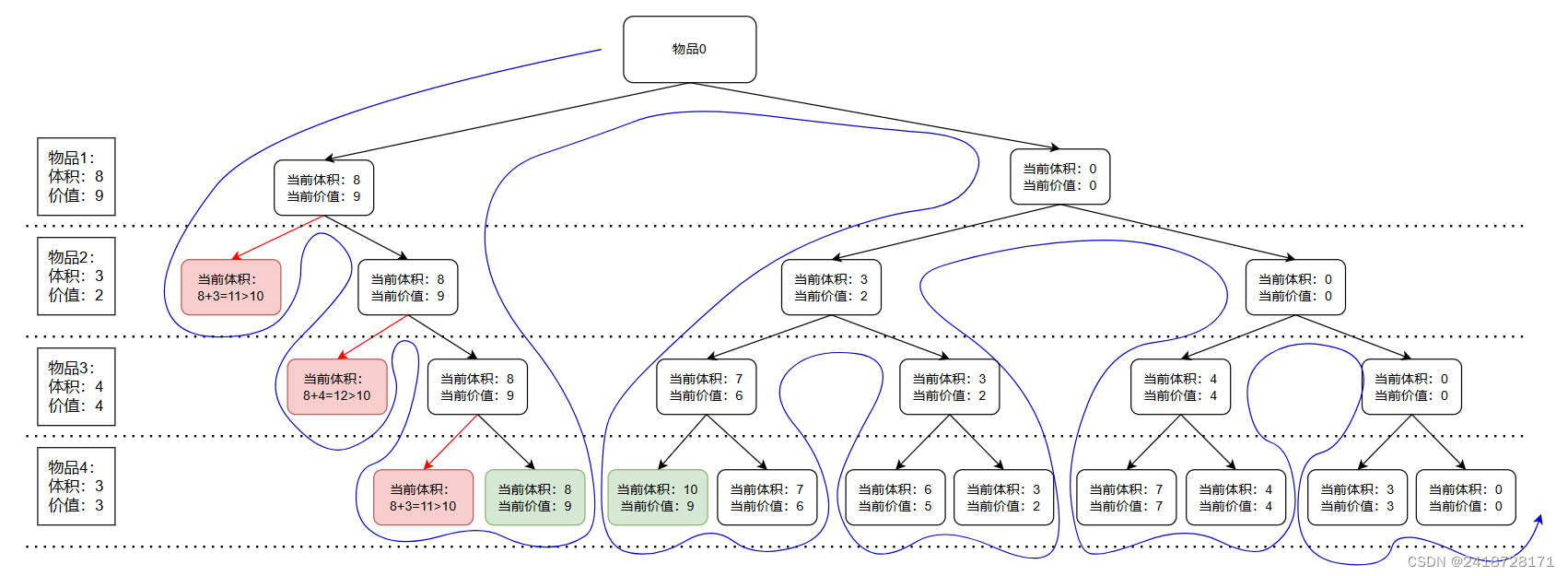
2、选择和判断(剪枝)
边界:当当前物品为最后一个物品时,则到达叶子节点,递归结束。
选择:每一步递归,针对当前物品,都存在放与不放两个选择。
剪枝:如果放入当前物品,通过判断放入后当前物品的总体积是否超过总体积,如果超过就进行剪枝。
回溯:当当前状态的所有情况考虑完之后,进行回溯。
剪枝:
在第一个物品放入,第二个物品尝试放入时,发现放入第二个物品后,体积变为:8+3=11> 背包体积=10,所以,在第一、第二个物品放入,无论剩下的物品怎么放,都会超出背包体积,此时进行剪枝,减少了大量的计算。
对比蛮力法:对于1100、1101、1110、1111这四种情况,其都会去计算一次,发现超出背包容量再结束,而回溯则在计算1100时,发现超出背包容量就直接剪枝,后面的其他几种情况都不再计算。
回溯:
在计算了0111这种情况后,进行回溯,到达011这一步,然后计算0110,直接使用了011这一步的状态(当前体积7,当前价值6),在这个基础上计算0110。
对比蛮力法:在计算了0111后,再次计算0110这种情况时,还需要计算011的体积和价值,然而这一步在计算0111时,011状态的体积和价值就已经计算过了,蛮力法进行了重复计算,而回溯法则保存了之前的状态,减少了重复计算。
3、输出结果
在递归过程中,更新最大价值,最终输出,
4、代码实现
不需要真的去构建这颗二叉树,通过递归模拟二叉树即可。
public class ZeroOneBackpackBacktrack {
private static int maxValue = 0;
public static void main(String[] args) {
int maxVolume = 10;
Item[] items = new Item[]{
new Item(8, 9),
new Item(3, 2),
new Item(4, 4),
new Item(3, 3)};
execute(items, maxVolume);
System.out.println(maxValue);
}
public static void execute(Item[] items, int maxVolume) {
zeroOneBackpackBacktrack(items, maxVolume, 0, 0, 0);
}
public static void zeroOneBackpackBacktrack(Item[] items, int maxVolume, int index, int currentVolume, int currentValue) {
// 当前体积已经超出背包最大体积
if (currentVolume > maxVolume) return;
// 更新最大价值
maxValue = Math.max(currentValue, maxValue);
// 未到达最后一个物品
if (index < items.length) {
// 放入当前物品
zeroOneBackpackBacktrack(items, maxVolume, index + 1, currentVolume + items[index].getVolume(), currentValue + items[index].getValue());
// 不放入当前物品
zeroOneBackpackBacktrack(items, maxVolume, index + 1, currentVolume, currentValue);
}
}
}
class Item {
int volume;
int value;
public Item(int volume, int value) {
this.volume = volume;
this.value = value;
}
public int getValue() {
return value;
}
public int getVolume() {
return volume;
}
}
回溯法经典案例-N皇后图解
问题描述:
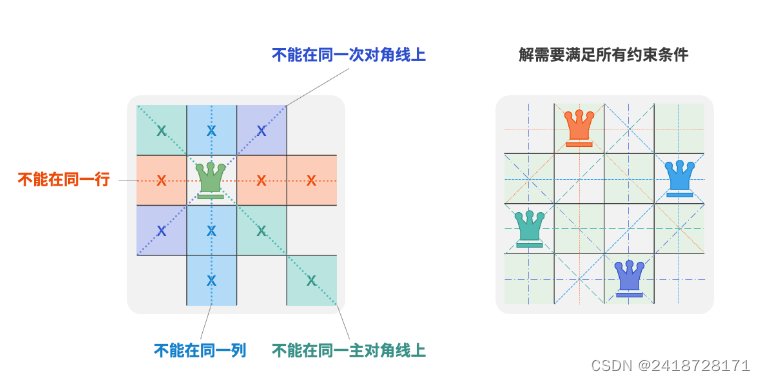
根据国际象棋的规则,皇后可以攻击与同处一行、一列或一条斜线上的棋子。给定 𝑛 个皇后和一个 𝑛×𝑛 大小的棋盘,寻找使得所有皇后之间无法相互攻击的摆放方案。
例如:
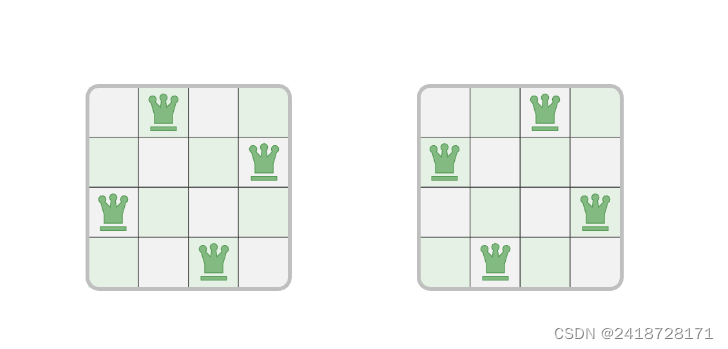
对于n = 4 的情况,有下面两种可能的摆放方法。
蛮力法:
蛮力法只需要将所有的情况都遍历到即可,对于每一行,尝试在每一列放置一个皇后,生成所有可能的放置方案。
每一行有n列,一共n行,遍历每种情况就需要 n ∗ n ∗ n . . . ∗ n = n n n*n*n...*n = n^n n∗n∗n...∗n=nn次,再加上每一次都要判断所有的皇后位置是否正确,又需要遍历。所以复杂度特别高。
public static void nQueens(int[][] data, int row) {
int n = data.length;
// 已经到达最后一行,n个皇后已经放置完毕
if (row == n) {
// 校验皇后拜访位置是否合理
for (int row1 = 0; row1 < n; row1++) {
for (int col = 0; col < n; col++) {
if (data[row1][col] == 1) {
// 判断每一行中皇后位置是否合理
if (!canPlace(data, row1, col)) {
// 不合理直接返回
return;
} else {
// 到达最后一行输出结果
if (row1 == n - 1) {
System.out.println("第" + ++num + "组解:");
for (int[] d : data) {
System.out.println(Arrays.toString(d));
}
}
}
}
}
}
}else{
// 未到达最后一行,遍历
for (int col = 0; col < n; col++) {
data[row][col] = 1;
nQueens(data, row + 1);
data[row][col] = 0;
}
}
}
public static boolean canPlace(int[][] data, int row, int col) {
// 检查同一列是否有皇后
for (int i = 0; i < row; i++) {
if (data[i][col] == 1) return false;
}
// 检查 \ 对角线是否存在皇后
for (int i = 1; row - i >= 0 && col - i >= 0; i++) {
if (data[row - i][col - i] == 1) return false;
}
// 检查 / 对角线是否存在皇后
for (int i = 1; row - i >= 0 && col + i < data.length; i++) {
if (data[row - i][col + i] == 1) return false;
}
return true;
}
回溯法:
1、定义问题并构造状态空间树
根据棋盘大小 n ∗ n n*n n∗n和 n n n个皇后,以及皇后可以攻击与其处于同一行上的其他皇后可知,每一行仅允许放置一个皇后。可以按照逐行放置的思路:从第一行开始,在每行放置一个皇后,直至最后一行结束。
那么每一行实际上就有n个选择,每个位置是否放入皇后,放入皇后之后,就可以进入下一行放置下一个皇后。
采用一个n叉树就可以表示,这里使用一个二维数组表示:
public static void dfs(int[][] data, int row) {
for (int col = 0; col < data.length; col++) {
// 放入皇后
data[row][col] = 1;
// 放入下一个皇后
dfs(data, row + 1);
// 取出当前皇后(回溯):每一行只能放置一个,取出当前列皇后,下一列放入
data[row][col] = 0;
}
}
}
2、选择和判断(剪枝)
在某一行的某一列放置皇后时,可能会出现如果该位置放置皇后,就会与前几行放置的皇后冲突,那么就可以提前剪枝,直接不用放置后续的皇后了,直接去尝试再下一列放置。
public static void dfs(int[][] data, int row) {
for (int col = 0; col < data.length; col++) {
// 剪枝:判断该位置是否可以放入,不可放入则直接终止
if (canPlace(data, row, col)) {
// 放入皇后
data[row][col] = 1;
// 放入下一个皇后
dfs(data, row + 1);
// 取出当前皇后(回溯):每一行只能放置一个,取出当前列皇后,下一列放入
data[row][col] = 0;
}
}
}
public static boolean canPlace(int[][] data, int row, int col) {
// 检查同一列是否有皇后
for (int i = 0; i < row; i++) {
if (data[i][col] == 1) return false;
}
// 检查 \ 对角线是否存在皇后
for (int i = 1; row - i >= 0 && col - i >= 0; i++) {
if (data[row - i][col - i] == 1) return false;
}
// 检查 / 对角线是否存在皇后
for (int i = 1; row - i >= 0 && col + i < data.length; i++) {
if (data[row - i][col + i] == 1) return false;
}
return true;
}
3、输出结果
当放置到最后一行时,此时所有皇后均放入,可以输出结果
public static void dfs(int[][] data, int row) {
// 最后一个皇后已经放入
if (row == data.length) {
printResult(data, ++resultNum);
return;
}
for (int col = 0; col < data.length; col++) {
// 剪枝:判断该位置是否可以放入,不可放入则直接终止
if (canPlace(data, row, col)) {
// 放入皇后
data[row][col] = 1;
// 放入下一个皇后
dfs(data, row + 1);
// 取出当前皇后(回溯):每一行只能放置一个,取出当前列皇后,下一列放入
data[row][col] = 0;
}
}
}
public static void printResult(int[][] data, int num) {
System.out.println("第" + num + "组解:");
for (int i = 0; i < data.length; i++) {
System.out.println(Arrays.toString(data[i]));
}
}
图解说明:
因为八皇后如果画图篇幅过大,这里用四皇后讲解:
其中白色表示尚未遍历,绿色表示放入皇后,红色表示被剪枝(此路不通)
1、给第一行第一列放入皇后,进入第二行在第二行第一列放入皇后,剪枝
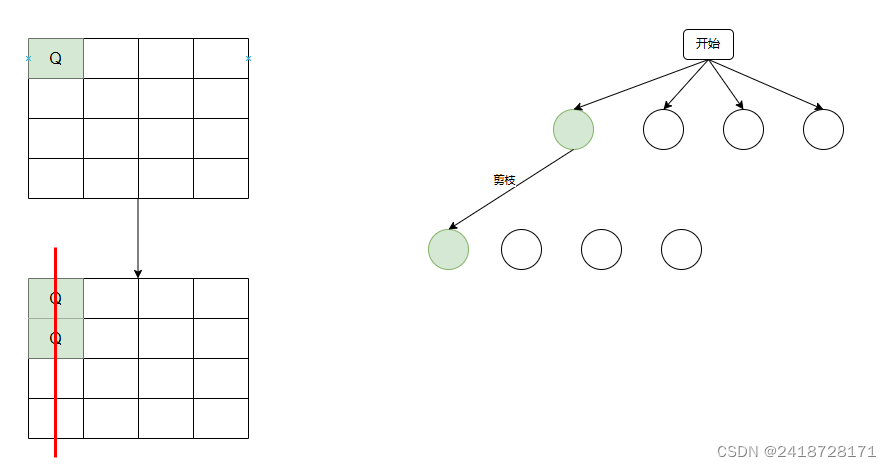
2、放入第二行第二列,剪枝
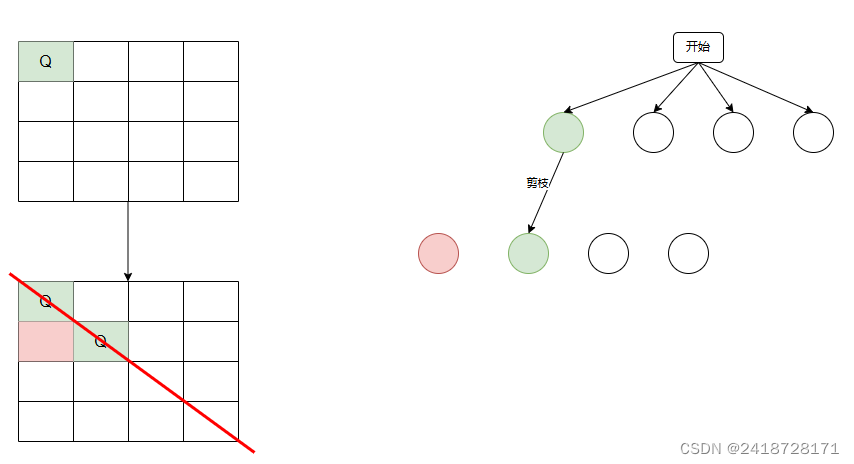
3、放入第二行第三列,皇后可以放置,再尝试放入第三行
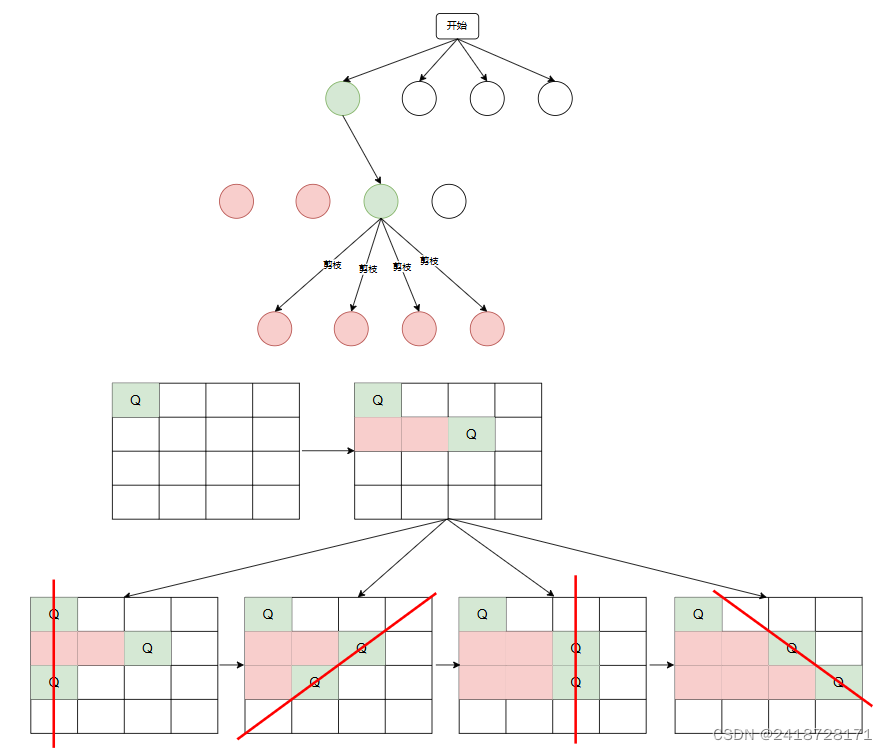
4、第二行第三列放入皇后的所有情况均被剪枝,放入第二行第四列
放入第三行第一列时剪枝,放入第三行第二列
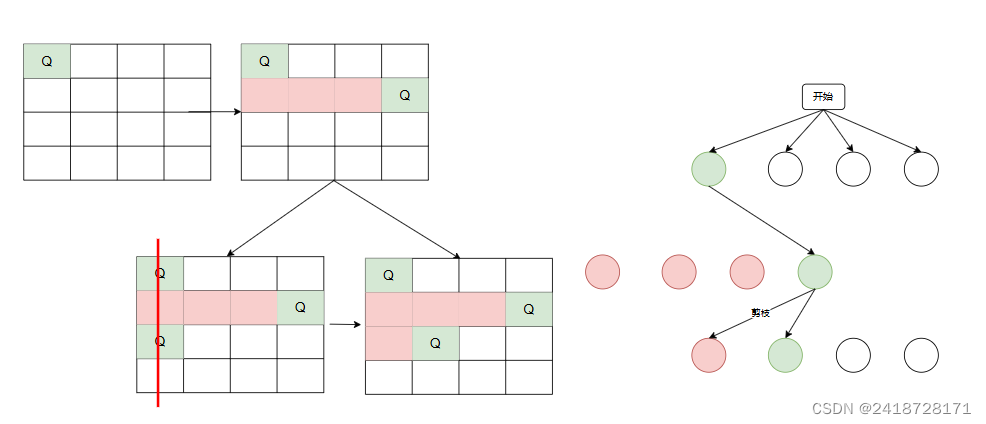
5、第三行确定后,放入第四行(最后一个皇后)
可见,在第四行第三列放入皇后时,符合要求,直接输出结果,其他几种情况均不符合情况
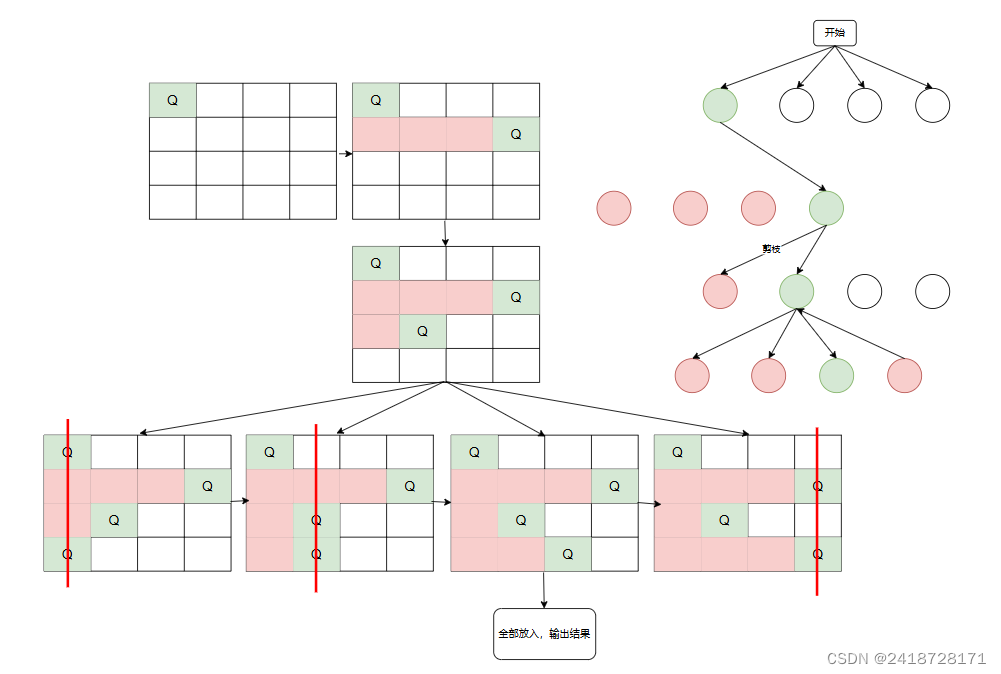
6、回溯,计算第三行放入第三列的情况
7、重复上述步骤
具体流程下图:
可以看到,这其实就是深度优先搜索,添加了剪枝
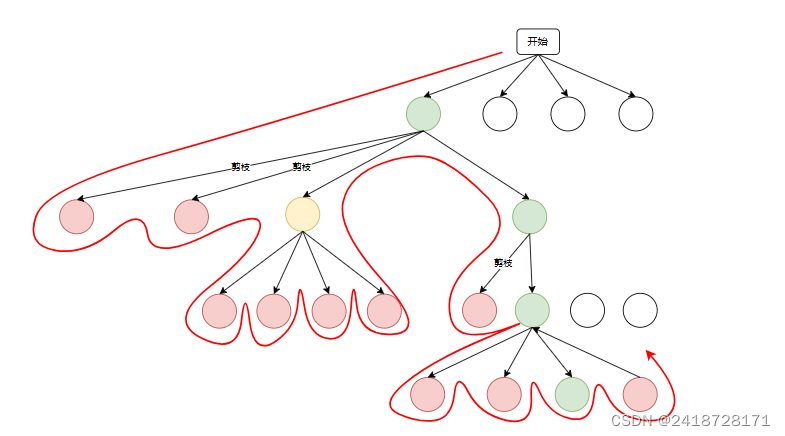
优化:
上面在判断某个位置是否可以放置皇后时,使用的计算过方式需要遍历,会导致每次计算时复杂度较高。
public static boolean canPlace(int[][] data, int row, int col) {
// 检查同一列是否有皇后
for (int i = 0; i < row; i++) {
if (data[i][col] == 1) return false;
}
// 检查 \ 对角线是否存在皇后
for (int i = 1; row - i >= 0 && col - i >= 0; i++) {
if (data[row - i][col - i] == 1) return false;
}
// 检查 / 对角线是否存在皇后
for (int i = 1; row - i >= 0 && col + i < data.length; i++) {
if (data[row - i][col + i] == 1) return false;
}
return true;
}
可以改为如下方式:
可以利用一个长度为 𝑛 的布尔型数组 existCol 记录每一列是否有皇后。在每次决定放置前,我们通过 cols 将已有皇后的列进行剪枝,并在回溯中动态更新 cols 的状态。
那么,如何处理对角线约束呢?
设棋盘中某个格子的行列索引为 (𝑟𝑜𝑤,𝑐𝑜𝑙) ,选定矩阵中的某条主对角线,我们发现该对角线上所有格子的行索引减列索引都相等,即对角线上所有格子的 𝑟𝑜𝑤−𝑐𝑜𝑙 为恒定值。
也就是说,如果两个格子满足 𝑟𝑜𝑤1−𝑐𝑜𝑙1=𝑟𝑜𝑤2−𝑐𝑜𝑙2 ,则它们一定处在同一条主对角线上。利用该规律,我们可以借助如图所示的数组 existLeftDiagonal 记录每条主对角线上是否有皇后。
容易看出,记录某一列是否有皇后的数组existLeftDiagonal长度为2N-1。
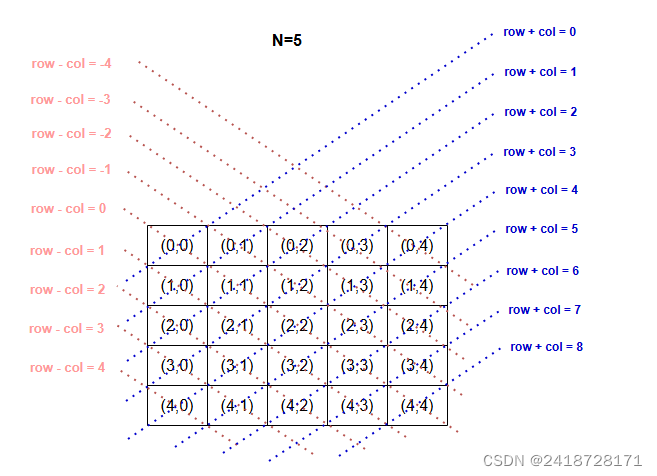
同理,次对角线上的所有格子的 𝑟𝑜𝑤+𝑐𝑜𝑙 是恒定值。我们同样也可以借助数组 existRightDiagonal 来处理次对角线约束。
public static boolean canPlace(int row, int col, int n, boolean[] existCol, boolean[] existLeftDiagonal, boolean[] existRightDiagonal) {
return !(existCol[col] ||
existLeftDiagonal[row - col + n - 1] ||
existRightDiagonal[row + col]);
}
完整代码:
package backtracking;
import java.util.Arrays;
public class EightQueens2 {
private static int num = 0;
public static void main(String[] args) {
execute(9);
}
public static void execute(int n) {
// 皇后存在情况表
int[][] data = new int[n][n];
// 皇后存在列情况
boolean[] existCol = new boolean[n];
// 皇后存在对角线 \ 情况 (可以发现处于同一对角线的元素,行 - 列是同一个值,所以可以使用这个性质来存储对角线信息)
boolean[] existLeftDiagonal = new boolean[2 * n - 1];
// 皇后存在对角线 / 情况(可以发现处于同一对角线的元素,行+ 列是同一个值,所以可以使用这个性质来存储对角线信息)
boolean[] existRightDiagonal = new boolean[2 * n - 1];
dfs(data, n, 0, existCol, existLeftDiagonal, existRightDiagonal);
}
private static void dfs(int[][] data, int n, int row, boolean[] existCol, boolean[] existLeftDiagonal, boolean[] existRightDiagonal) {
if (row == n) {
// 所有皇后已放置完毕,输出
printResult(data, ++num);
}
for (int col = 0; col < n; col++) {
// 剪枝:判断该位置是否可以放入,不可放入则直接终止
if (canPlace(row, col, n, existCol, existLeftDiagonal, existRightDiagonal)) {
// 放入皇后
placeQueen(row, col, n, data, existCol, existLeftDiagonal, existRightDiagonal);
// 放入下一个皇后
dfs(data, n, row + 1, existCol, existLeftDiagonal, existRightDiagonal);
// 取出皇后
cancelPlaceQueen(row, col, n, data, existCol, existLeftDiagonal, existRightDiagonal);
}
}
}
public static boolean canPlace(int row, int col, int n, boolean[] existCol, boolean[] existLeftDiagonal, boolean[] existRightDiagonal) {
return !(existCol[col] || existLeftDiagonal[row - col + n - 1] || existRightDiagonal[row + col]);
}
public static void placeQueen(int row, int col, int n, int[][] data, boolean[] existCol, boolean[] existLeftDiagonal, boolean[] existRightDiagonal) {
data[row][col] = 1;
existCol[col] = existLeftDiagonal[row - col + n - 1] = existRightDiagonal[row + col] = true;
}
public static void cancelPlaceQueen(int row, int col, int n, int[][] data, boolean[] existCol, boolean[] existLeftDiagonal, boolean[] existRightDiagonal) {
data[row][col] = 0;
existCol[col] = existLeftDiagonal[row - col + n - 1] = existRightDiagonal[row + col] = false;
}
public static void printResult(int[][] data, int num) {
System.out.println("第" + num + "组解:");
for (int[] d : data) {
System.out.println(Arrays.toString(d));
}
}
}



![Spring学习01-[Spring实现IOC的几种方式]](https://img-blog.csdnimg.cn/direct/3f138876749d44a289a60d4050cd2db7.png)