52. 携带研究材料（第七期模拟笔试）

小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的重量，并且具有不同的价值。

小明的行李箱所能承担的总重量为 N，问小明应该如何抉择，才能携带最大价值的研究材料，每种研究材料可以选择无数次，并且可以重复选择。

输入描述
第一行包含两个整数，N，V，分别表示研究材料的种类和行李空间

接下来包含 N 行，每行两个整数 wi 和 vi，代表第 i 种研究材料的重量和价值

输出描述
输出一个整数，表示最大价值。
输入示例
4 5
1 2
2 4
3 4
4 5
输出示例
10

方法一：

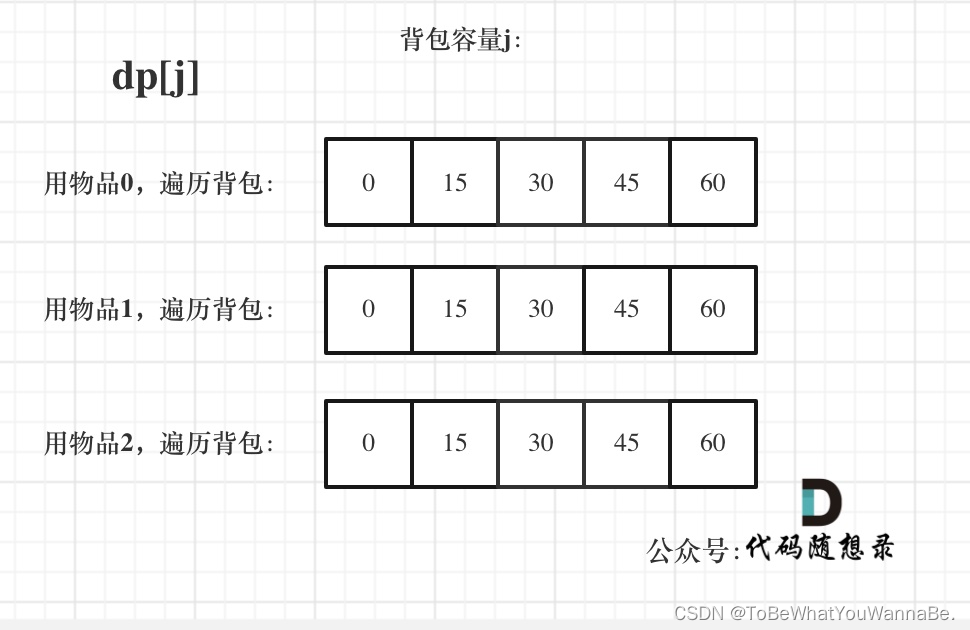
//先遍历物品，再遍历背包
private static void testCompletePack(){
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWeight = 4;
    int[] dp = new int[bagWeight + 1];
    for (int i = 0; i < weight.length; i++){ // 遍历物品
        for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    for (int maxValue : dp){
        System.out.println(maxValue + "   ");
    }
}

这段代码是一个使用动态规划解决0-1背包问题的Java示例。0-1背包问题是指有N件物品和一个容量为W的背包，每种物品都有自己的重量和价值，在不超过背包所能装载的总重量的前提下，如何选择装入背包的物品，使得背包中物品的总价值最大。

代码解释如下：

1. 定义了物品的重量数组 weight 和价值数组 value，以及背包的最大容量 bagWeight。
2. 创建一个数组 dp，长度为 bagWeight + 1，用于存储每个背包容量下的最大价值。初始化时，默认值都为0，表示背包为空时的价值为0。
3. 外层循环（for (int i = 0; i < weight.length; i++)）遍历每一件物品。
4. 内层循环（for (int j = weight[i]; j <= bagWeight; j++)）遍历从当前物品的重量开始到背包最大容量的所有可能的背包容量。这样设置是因为如果背包容量小于当前物品的重量，这件物品不可能被放入背包中，所以不必考虑。
5. 在内层循环中，使用 Math.max() 函数比较两种情况：一是不把当前物品放入背包中时的最大价值 dp[j]，二是把当前物品放入背包后剩余空间的最大价值 dp[j - weight[i]] + value[i]，取两者的较大值作为新的 dp[j]，即更新这个背包容量下的最大价值。
6. 最后，通过遍历并打印数组 dp，可以得到不同背包容量下能够达到的最大价值。

这段代码执行后，会输出一个序列，表示从容量为0到容量为bagWeight的背包能够装入物品的最大价值。最后一项即为给定背包容量下的最大价值。

方法二：

//先遍历背包，再遍历物品
private static void testCompletePackAnotherWay(){
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWeight = 4;
    int[] dp = new int[bagWeight + 1];
    for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
        for (int j = 0; j < weight.length; j++){ // 遍历物品
            if (i - weight[j] >= 0){
                dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
            }
        }
    }
    for (int maxValue : dp){
        System.out.println(maxValue + "   ");
    }
}

这段代码同样是解决0-1背包问题的Java实现，但它的遍历顺序与上一个示例相反：首先遍历背包的容量，然后遍历物品。下面是这段代码的解释：

1. 定义变量：与前一个示例相同，定义了物品的重量数组 weight、价值数组 value 以及背包的最大容量 bagWeight。同时初始化了一个 dp 数组来记录不同背包容量下的最大价值。

2. 外层循环 (for (int i = 1; i <= bagWeight; i++))：这次是先从背包容量为1开始，直到遍历到最大背包容量 bagWeight。这里从1开始是因为容量为0的情况在初始化时已经设定为0，无需处理。

3. 内层循环 (for (int j = 0; j < weight.length; j++))：遍历每一个物品。与前一个示例的遍历顺序相反。

4. 条件判断 (if (i - weight[j] >= 0))：在尝试将当前物品放入背包之前，先检查当前背包的容量 i 是否至少能放下物品 j。这是必要的，因为如果背包容量不足以容纳当前物品，就无需继续计算加入该物品后的价值，直接跳过。

5. 价值更新：如果背包容量足够，使用 Math.max() 函数比较当前背包容量下的最大价值 dp[i] 和将当前物品放入背包后剩余空间的最大价值加上当前物品的价值 dp[i - weight[j]] + value[j]，取较大者作为新的 dp[i]。这一步确保了在考虑添加新物品时，背包的价值总是尽可能大。

6. 输出结果：最后，遍历并打印数组 dp，展示不同背包容量下可达到的最大价值。最后一项依然是整个问题的解，即背包最大容量为 bagWeight 时能够装入物品的最大总价值。

这种遍历顺序（先背包容量，后物品）也是解决0-1背包问题的有效方法，它在逻辑上直观地体现了“逐渐增加背包容量并尝试放入所有物品以最大化价值”的过程。

518. 零钱兑换 II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

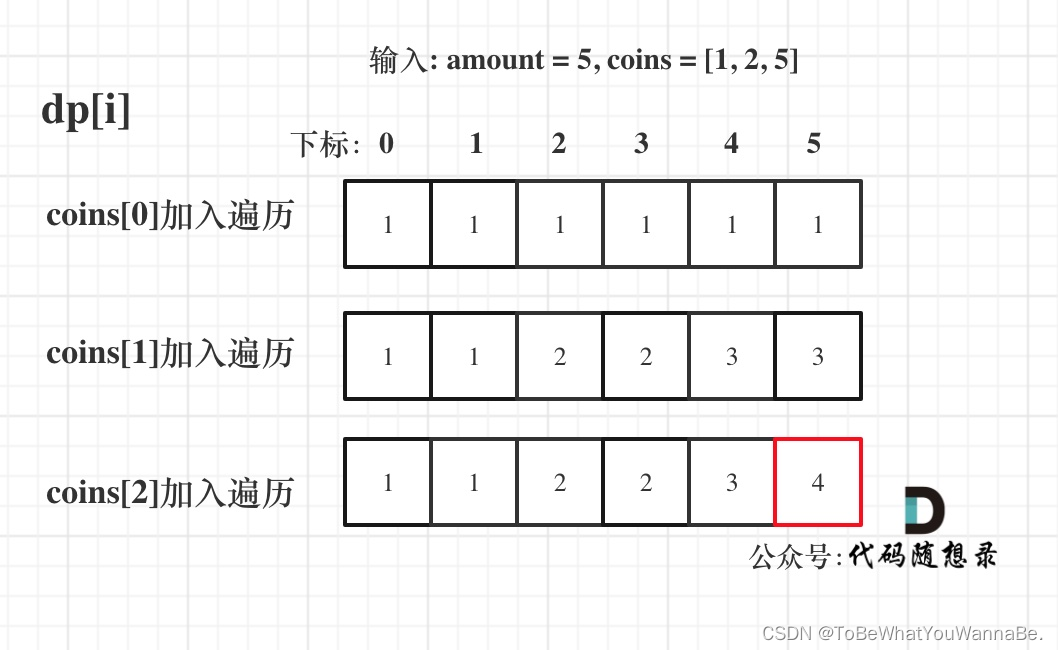
输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2：

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。
示例 3：

输入：amount = 10, coins = [10]
输出：1

方法一：

class Solution {
    public int change(int amount, int[] coins) {
        //递推表达式
        int[] dp = new int[amount + 1];
        //初始化dp数组，表示金额为0时只有一种情况，也就是什么都不装
        dp[0] = 1;
        for (int i = 0; i < coins.length; i++) {
            for (int j = coins[i]; j <= amount; j++) {
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}

这段代码是Java语言实现的一个解决方案，解决的是找零问题（Coin Change Problem）。给定一定数量的硬币（每种硬币的数量不限）和一个总金额，求出有多少种不同的组合方式可以凑成总金额。这是一个经典的动态规划问题。

具体分析如下：

1. 定义状态：dp[j] 表示总额为 j 时的找零方案数。这是我们要填充的动态规划数组。

2. 初始化：dp[0] = 1，表示当金额为0时，有一种组合方式（即不选任何硬币）。

3. 双层循环：

   • 外层循环 for (int i = 0; i < coins.length; i++) 遍历每一种硬币。
   • 内层循环 for (int j = coins[i]; j <= amount; j++) 从当前硬币的面值开始，遍历到总金额。这是因为如果当前金额小于硬币的面值，不可能再用这个硬币去凑更小的金额，所以从硬币面值开始是有意义的起始点。

4. 状态转移方程：dp[j] += dp[j - coins[i]]。对于每一个 j，都有两种情况：要么使用当前硬币 coins[i]，那么剩余的金额就是 j - coins[i]，方案数就是 dp[j - coins[i]]；要么不使用当前硬币，直接继承之前的方案数 dp[j]。但因为我们要累加所有可能的组合，所以是累加而不是直接赋值。

5. 返回结果：最后返回 dp[amount]，即为目标总金额的找零方案数。

综上所述，这段代码通过动态规划的方法，高效地计算出了给定硬币种类和总金额下的找零组合数。

方法二：

// 二维dp数组版本，方便理解
class Solution {
    public int change(int amount, int[] coins) {
        int[][] dp = new int[coins.length][amount+1];

        // 初始化边界值
        for(int i = 0; i < coins.length; i++){
            // 第一列的初始值为1
            dp[i][0] = 1;
        }
        for(int j = coins[0]; j <= amount; j++){
            // 初始化第一行
            dp[0][j] += dp[0][j-coins[0]];
        }
        
        for(int i = 1; i < coins.length; i++){
            for(int j = 1; j <= amount; j++){
                if(j < coins[i]) dp[i][j] = dp[i-1][j];
                else dp[i][j] = dp[i][j-coins[i]] + dp[i-1][j];
            }
        }

        return dp[coins.length-1][amount];
    }
}

这段代码是另一个版本的解决方案，同样用来解决找零问题（Coin Change Problem），但是使用了二维动态规划数组来实现，这有助于更直观地理解动态规划的状态转移过程。下面是对代码的详细解析：

1. 初始化二维dp数组：int[][] dp = new int[coins.length][amount+1];，其中 dp[i][j] 表示在前 i+1 种硬币中选取，凑成总额为 j 的组合数。

2. 初始化边界值：

   • 对于每一行（每种硬币）的首列（总额为0的情况），都只有1种方法，即不选择任何硬币，因此 dp[i][0] = 1;。
   • 初始化第一行时，需要根据第一种硬币的不同面额来填充。对于每一列 j（从硬币面值开始到总金额），如果可以由若干个第一种硬币组成，即 j >= coins[0]，则 dp[0][j] += dp[0][j-coins[0]]，意味着可以通过在已有的组合基础上再添加一个硬币来得到这个总额。

3. 状态转移：核心的双层循环遍历每一种硬币和每一个可能的总金额。

   • 对于 i > 0（即除了第一种硬币之外的其他硬币）和 j > 0（即除了总额为0之外的情况），有两种选择：
     • 不使用第 i 种硬币，这时的组合数与前 i-1 种硬币凑成总额 j 的组合数相同，即 dp[i][j] = dp[i-1][j]。
     • 使用至少一个第 i 种硬币，剩余的金额为 j - coins[i]，这时的组合数是在总额减去当前硬币面值后，使用全部 i 种硬币的组合数，即 dp[i][j-coins[i]]。因此，这两种情况的组合数相加即为最终的 dp[i][j]。
     • 注意，当 j < coins[i]，即当前总额无法再使用第 i 种硬币时，不应考虑使用该硬币的情况，直接继承前 i-1 种硬币的结果。

4. 返回结果：最终答案为 dp[coins.length-1][amount]，即在所有硬币中选择，凑成总金额为 amount 的所有可能组合数。

这个版本虽然占用更多的空间，但它清晰地展现了每一步决策的过程，便于理解和分析动态规划的状态转移逻辑。

377. 组合总和 Ⅳ

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。
示例 2：

输入：nums = [9], target = 3
输出：0

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        for (int i = 0; i <= target; i++) {
            for (int j = 0; j < nums.length; j++) {
                if (i >= nums[j]) {
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
}

这段代码是用来解决完全背包问题（Unbounded Knapsack Problem）的一个变种——求解组合总和IV的问题。给定一个由正整数组成的数组 nums 和一个目标整数 target，找出并返回可以由 nums 中的数字组成的、和为目标整数 target 的不同非空组合的数量。每个数组中的数字可以无限制次数地重复被选取。

这里是使用一维动态规划的解决方案，具体解析如下：

1. 初始化dp数组：int[] dp = new int[target + 1];，其中 dp[i] 表示总和为 i 的组合数。初始化 dp[0] = 1，表示总和为0的情况只有一个组合（即不选任何数）。

2. 双层循环：

   • 外层循环 for (int i = 0; i <= target; i++) 遍历从0到目标值 target 的每一个可能的总和。
   • 内层循环 for (int j = 0; j < nums.length; j++) 遍历数组 nums 中的所有数字。

3. 状态转移：对于每个总和 i，考虑数组中的每个数 nums[j]，如果当前总和 i 大于等于这个数（i >= nums[j]），说明可以使用 nums[j] 来构成总和 i 的一部分，那么 dp[i] 应该加上总和为 i - nums[j] 时的组合数，即 dp[i] += dp[i - nums[j]]。这样就实现了从已知的较小问题的解来构建更大问题解的过程。

4. 返回结果：最终答案是 dp[target]，即所有元素和为目标值 target 的组合总数。

这个解法有效地利用了动态规划避免了重复计算，降低了时间复杂度。其时间复杂度大致为O(n * target)，其中n为数组 nums 的长度，target为所求的目标和。

57. 爬楼梯（第八期模拟笔试）

题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

输入描述
输入共一行，包含两个正整数，分别表示n, m
输出描述
输出一个整数，表示爬到楼顶的方法数。
输入示例
3 2
输出示例
3

import java.util.Scanner;
class climbStairs{
    public static void main(String [] args){
        Scanner sc = new Scanner(System.in);
        int m, n;
        while (sc.hasNextInt()) {
            // 从键盘输入参数，中间用空格隔开
            n = sc.nextInt();
            m = sc.nextInt();

            // 求排列问题，先遍历背包再遍历物品
            int[] dp = new int[n + 1];
            dp[0] = 1;
            for (int j = 1; j <= n; j++) {
                for (int i = 1; i <= m; i++) {
                    if (j - i >= 0) dp[j] += dp[j - i];
                }
            }
            System.out.println(dp[n]);
        }
    }
}

这段Java代码实现了一个爬楼梯问题的解法，不过这里的描述有误，实际上解决的是完全背包问题的一个变形，而非直接的爬楼梯问题。但我们可以按照代码逻辑来理解它所解决的问题：给定一个人可以一次跳跃1到m个台阶，问他有多少种不同的方式跳上n阶楼梯。

解析如下：

1. 导入Scanner类：用于从控制台读取用户输入的数据。
2. 定义主函数：在主函数中，程序通过Scanner对象sc读取两个整数，分别代表楼梯阶数n和每次跳跃的最大阶数m。
3. 初始化动态规划数组：创建一个大小为n+1的数组dp，其中dp[j]表示到达第j阶楼梯的不同方法数。初始化dp[0]=1，表示站在起点（0阶）只有1种方法（即不跳）。
4. 双层循环：
   • 外层循环for (int j = 1; j <= n; j++)遍历从第1阶到第n阶楼梯。
   • 内层循环for (int i = 1; i <= m; i++)遍历每次跳跃的阶数，从1跳到m。
   • 如果当前阶数j大于或等于跳跃的阶数i，则可以从j-i阶跳到第j阶，因此dp[j]需要累加dp[j-i]，即之前阶数到达方式的总数。
5. 输出结果：最后，输出dp[n]，即到达第n阶楼梯的所有不同方法数。

尽管注释提到“求排列问题，先遍历背包再遍历物品”，但实际上这段代码解决的是一个组合问题，更准确地说是完全背包问题的一种特殊情况，用来计算在给定步长限制下到达特定楼层的方案数。