在开始学习堆之前,我们要先简单了解二叉树
二叉树
一棵二叉树是结点的一个有限集合,该集合:
- 为空
- 由一个根结点加上两棵子树(左子树和右子树)
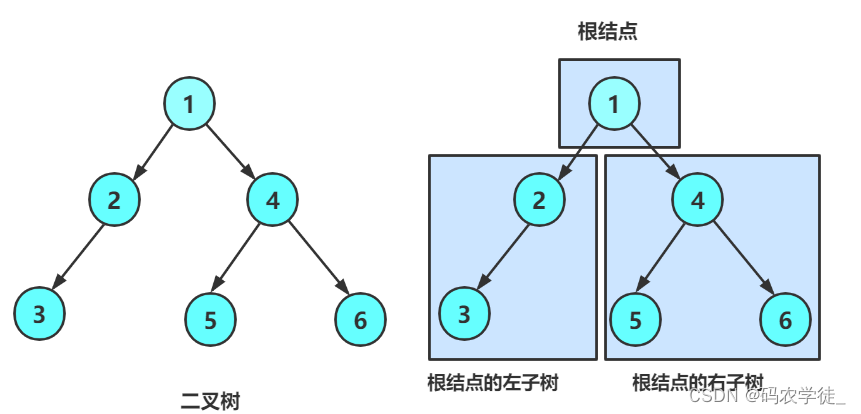
特殊的二叉树:
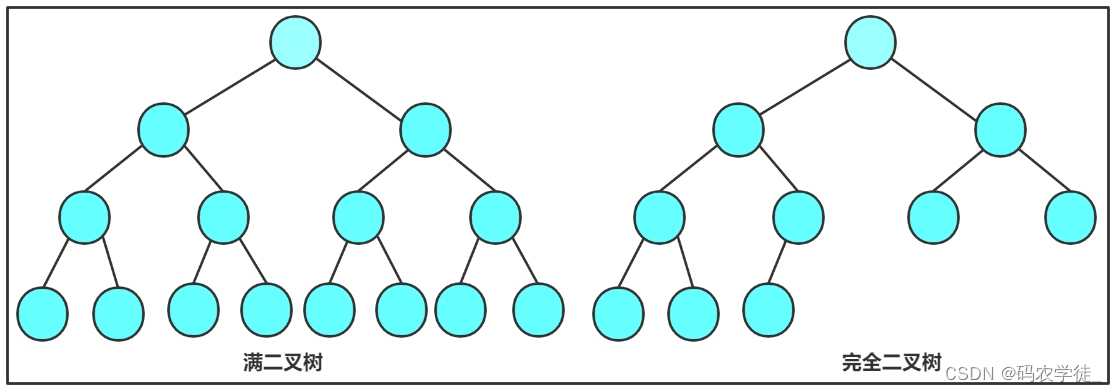
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 (2^k)-1,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K
的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
堆
堆就是上面描述的完全二叉树的一种,完全二叉树就是除了最后一层外,其他层节点数达到最大。
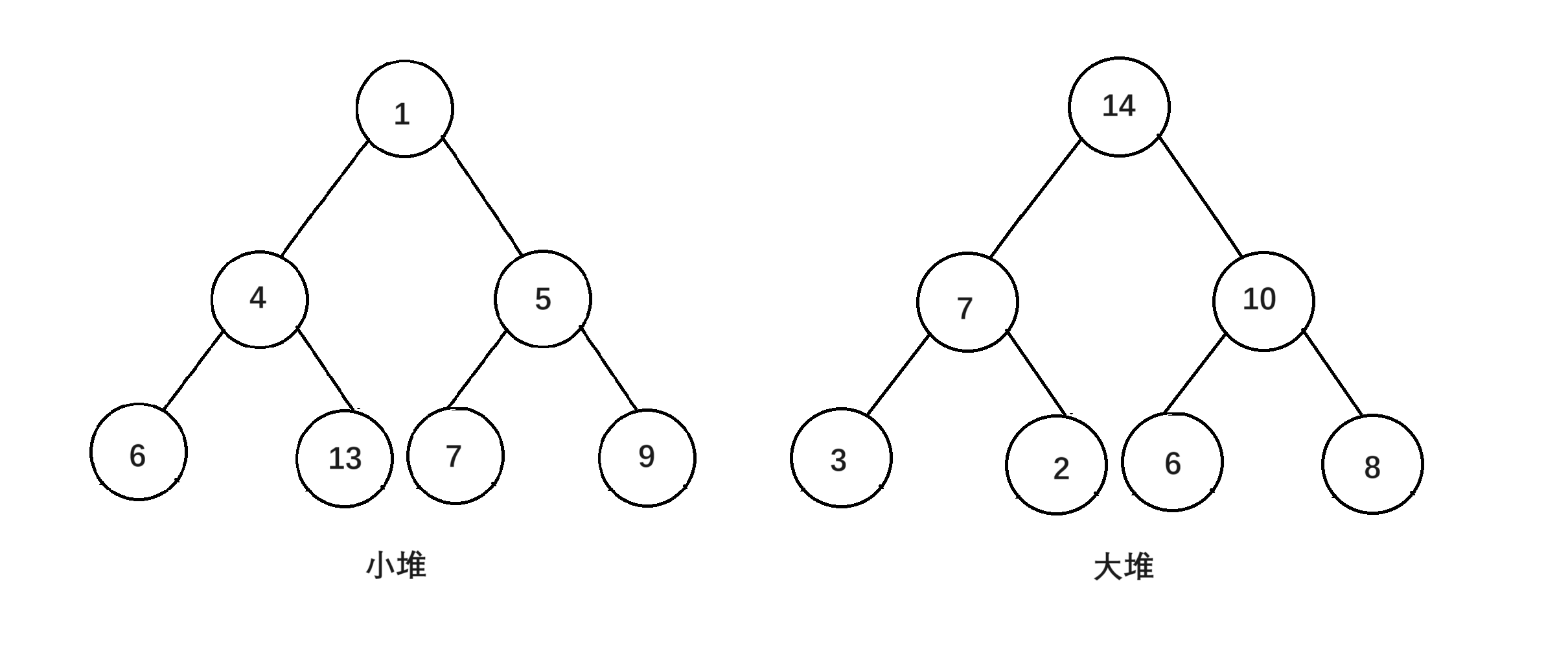
堆与普通的完全二叉树结构相似,但存在大小堆的性质
-
大堆:树任何一个父节点>=子节点
-
小堆:树任何一个父节点<=子节点
堆的主要操作包括:
- 插入:将新元素添加到堆中,同时保持堆的性质。
- 删除堆顶元素:删除堆顶元素,同时保持堆的性质。
- 获取堆顶元素值:返回堆顶元素的值但不删除它。
- 调整堆(向上调整/向下调整):将一个数组或部分数组调整成堆的形状。
堆一些应用实例:
- 堆排序(Heap Sort):堆排序算法利用堆数据结构对数组进行排序。它的时间复杂度为O(NlogN),在特定情况下,它可能比快速排序还要快。
- 优先队列(Priority Queue):在任务调度等场景中,堆可以作为优先队列实现,确保优先级高的任务先执行。
- 快速查找问题:例如,在大量数据中找出前K个最大或最小的元素,尤其是在内存受限的情况下,堆是一个有效的解决方案。
堆的实现
我们今天实现一个小堆,并利用这个小堆实现一个简单的堆排序。
首先创建三个文件:
Heap.h —— 用于声明函数的头文件。
Heap.c —— 堆主要函数的实现。
test.c——测试堆,并实现简单堆排序。
创建堆
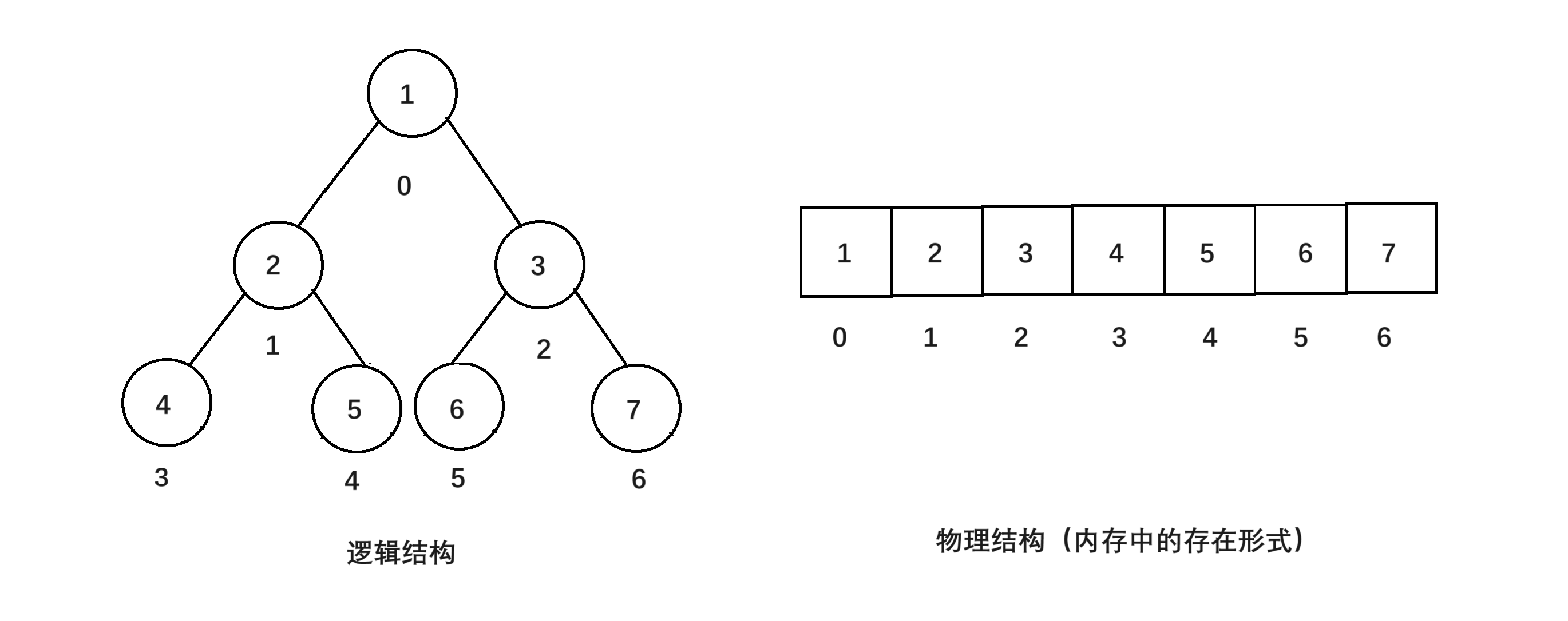
堆在逻辑上是二叉树的结构,但在实际上是数组结构
typedef int HPDataType;//方便后需更改数据类型
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
堆的初始化
//堆的初始化
void HeapInit(Heap* hp)
{
assert(hp);
hp->_a = NULL;
hp->_capacity = hp->_size = 0;
}
堆的销毁
// 堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp->_a);
hp->_a = NULL;
hp->_capacity = hp->_size = 0;
}
调整堆
交换数据
单独封装交换函数便于使用
//交换数据
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType* tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
向上调整
因为我们要建立小堆,在插入数据后(尾插)我们要调整这个数据的位置,使它满足小堆的性质,也就是父节点>=子节点。所以只要遇到父节点<子节点的情况,我们就交换这两个节点,然后向上更新父亲和孩子的位置,继续循环查看父节点<子节点的情况,直到这个插入的数据到达正确的地方。
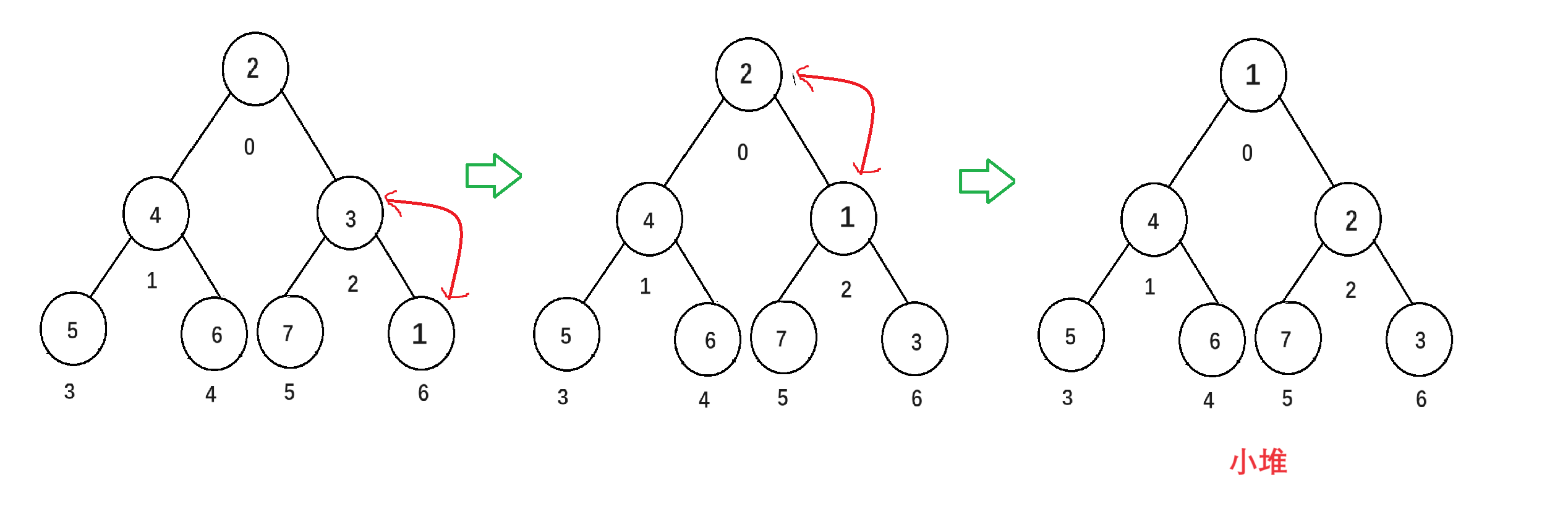
//向上调整
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);//交换节点
//更新父亲和孩子的位置
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
向下调整
因为我们要建立小堆,在删除堆顶元素时,我们需要将堆顶和堆尾交换位置然后删除堆尾,为了满足小堆的性质,也就是父节点>=子节点。所以从堆顶向下只要遇到父节点<子节点的情况,我们就交换这两个节点,然后向下更新父亲和孩子的位置,继续循环查看父节点<子节点的情况,直到交换上来的这个数据到正确的地方。
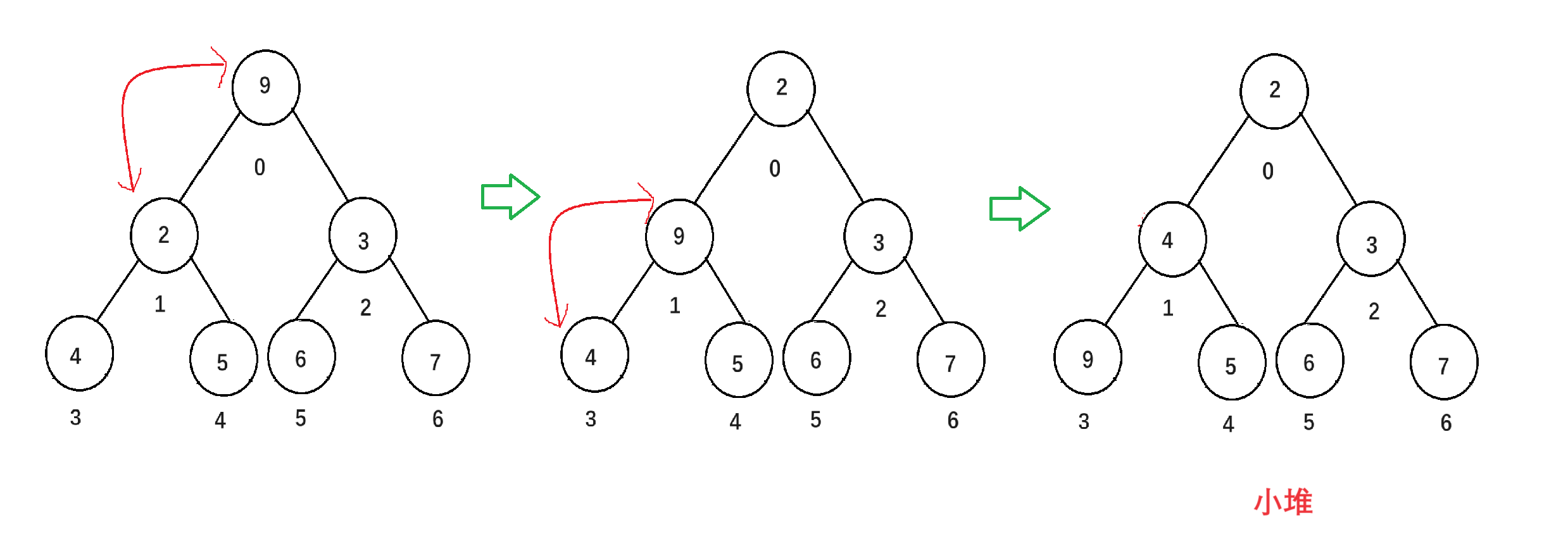
//向下调整
void AdjustDown(HPDataType* a, int n, int parent)//n是堆元素个数
{
int child = (parent * 2) + 1;//左孩子
while (child < n)
{//child+1<n防止越界访问
if ((child + 1 < n) && (a[child] > a[child + 1]))//假设法找出较小的孩子
child++;
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = (parent * 2) + 1;
}
else
{
break;
}
}
}
堆的插入
没有空间开辟空间,然后将数据尾插,再向上调整让小堆恢复其性质
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->_capacity == hp->_size)
{
int newcapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;
HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
perror("realloc");
exit(1);
}
hp->_capacity = newcapacity;
hp->_a = tmp;
}
hp->_a[hp->_size] = x;
hp->_size++;
AdjustUp(hp->_a, hp->_size - 1);
}
堆的删除
准确来说是删除堆顶,先将堆顶和堆尾交换,删除堆尾(原堆顶),再向下调整让其恢复小堆的性质。
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp);
assert(hp->_size>0);
Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
hp->_size--;
AdjustDown(hp->_a, hp->_size, 0);
}
取堆顶的数据
直接返回即可。
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp);
assert(hp->_size>0);
return hp->_a[0];
}
堆的数据个数
// 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);
return hp->_size;
}
堆的判空
返回size == 0时的结果,因为此时堆为空
// 堆的判空
int HeapEmpty(Heap* hp)
{
assert(hp);
return hp->_size == 0;
}
堆源码以及简单堆排序
Heap.h
#include<stdbool.h>
#include<assert.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
//堆的初始化
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
//向上调整
void AdjustUp(HPDataType* a, int child);
//向下调整
void AdjustDown(HPDataType* a, int n, int parent);
//交换数据
void Swap(HPDataType* p1, HPDataType* p2);
Heap.c
#include"Heap.h"
//堆的初始化
void HeapInit(Heap* hp)
{
assert(hp);
hp->_a = NULL;
hp->_capacity = hp->_size = 0;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);
free(hp->_a);
hp->_a = NULL;
hp->_capacity = hp->_size = 0;
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);
if (hp->_capacity == hp->_size)
{
int newcapacity = hp->_capacity == 0 ? 4 : 2 * hp->_capacity;
HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
perror("realloc");
exit(1);
}
hp->_capacity = newcapacity;
hp->_a = tmp;
}
hp->_a[hp->_size] = x;
hp->_size++;
AdjustUp(hp->_a, hp->_size - 1);
}
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp);
assert(hp->_size>0);
Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
hp->_size--;
AdjustDown(hp->_a, hp->_size, 0);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp);
assert(hp->_size>0);
return hp->_a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);
return hp->_size;
}
// 堆的判空
int HeapEmpty(Heap* hp)
{
assert(hp);
return hp->_size == 0;
}
//交换数据
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//向上调整
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = (parent * 2) + 1;
while (child < n)
{
if ((child + 1 < n) && (a[child] > a[child + 1]))
child++;
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = (parent * 2) + 1;
}
else
{
break;
}
}
}
text.c(简单堆排序)
创建一个堆,把一个数据混乱的数组插入到小堆中,然后循环打印堆顶数据(堆顶数据最小),再将堆顶数据删除,最后销毁堆。注意:这里的排序只是打印出来了排序的结果,数组内部并没有真正排序
#include"heap.h"
void heap1()
{
Heap hp;
HeapInit(&hp);
int arr[] = { 123,645,21433,45,24,7654,2,3,12,122 };
for (int i = 0; i < (sizeof(arr) / sizeof(int)); i++)
{
HeapPush(&hp, arr[i]);
}
while (!HeapEmpty(&hp))
{
printf("%d ", HeapTop(&hp));
HeapPop(&hp);
}
printf("\n");
HeapDestory(&hp);
}
int main()
{
heap1();
return 0;
}
排序结果
将大堆变成小堆
只需要将向上调整和向下调整中if (a[child] < a[parent])改为if (a[child] > a[parent])即可。