---

前言：

张量？张亮？张量是什么？

张量是一个可以用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数，张量作为一种特殊的数据结构，和数组和矩阵都有一定的相似性，是MindSpore网络运算中的基本数据结构。在本节当中主要介绍了张量以及稀疏张量的属性和用法。

今日所学：

1. 创建张量

其中第一部分讲述了创建张量，其包含了根据数据直接生成，从Numpy数组生成，使用init初始化器构造，继承另一个张量的属性，形成新的张量等方法来进行创建。
比如，直接由数据生成的方式如下：

data = [1, 0, 1, 0]
x_data = Tensor(data)print(x_data, x_data.shape, x_data.dtype)

结果如下：

使用init初始化器构造张量的方式如下代码：

from mindspore.common.initializer import One, Normal

# Initialize a tensor with ones
tensor1 = mindspore.Tensor(shape=(2, 2), dtype=mindspore.float32, init=One())
# Initialize a tensor from normal distribution
tensor2 = mindspore.Tensor(shape=(2, 2), dtype=mindspore.float32, init=Normal())

print("tensor1:\n", tensor1)
print("tensor2:\n", tensor2)

结果如下：

2. 张量的属性

第二个部分介绍了张量的属性，它的属性包括了形状、数据类型、转置张量、单个元素大小、占用字节数量、维数、元素个数和每一维步长等内容。
其属性事例如下：

x = Tensor(np.array([[1, 2], [3, 4]]), mindspore.int32)

print("x_shape:", x.shape)
print("x_dtype:", x.dtype)
print("x_itemsize:", x.itemsize)
print("x_nbytes:", x.nbytes)
print("x_ndim:", x.ndim)
print("x_size:", x.size)
print("x_strides:", x.strides)

结果如下：

3.张量索引与运算

然后介绍了张量索引以及张量的运算，其中索引与Numpy索引类似。对于张量的运算。有许多包含了算术、线性代数、矩阵处理、采样等多种运算。
其中普通的运算代码事例如下：

x = Tensor(np.array([1, 2, 3]), mindspore.float32)
y = Tensor(np.array([4, 5, 6]), mindspore.float32)output_add = x + youtput_sub = x - youtput_mul = x * youtput_div = y / xoutput_mod = y % xoutput_floordiv = y // xprint("add:", output_add)print("sub:", output_sub)print("mul:", output_mul)print("div:", output_div)print("mod:", output_mod)print("floordiv:", output_floordiv)

结果如下：

4. NumPy与Tensor的转换

将Tensor变量转换为NumPy变量，可以使用使用 Tensor.asnumpy() 来转换；
将NumPy变量转换为Tensor变量，可以使用Tensor()来转换。

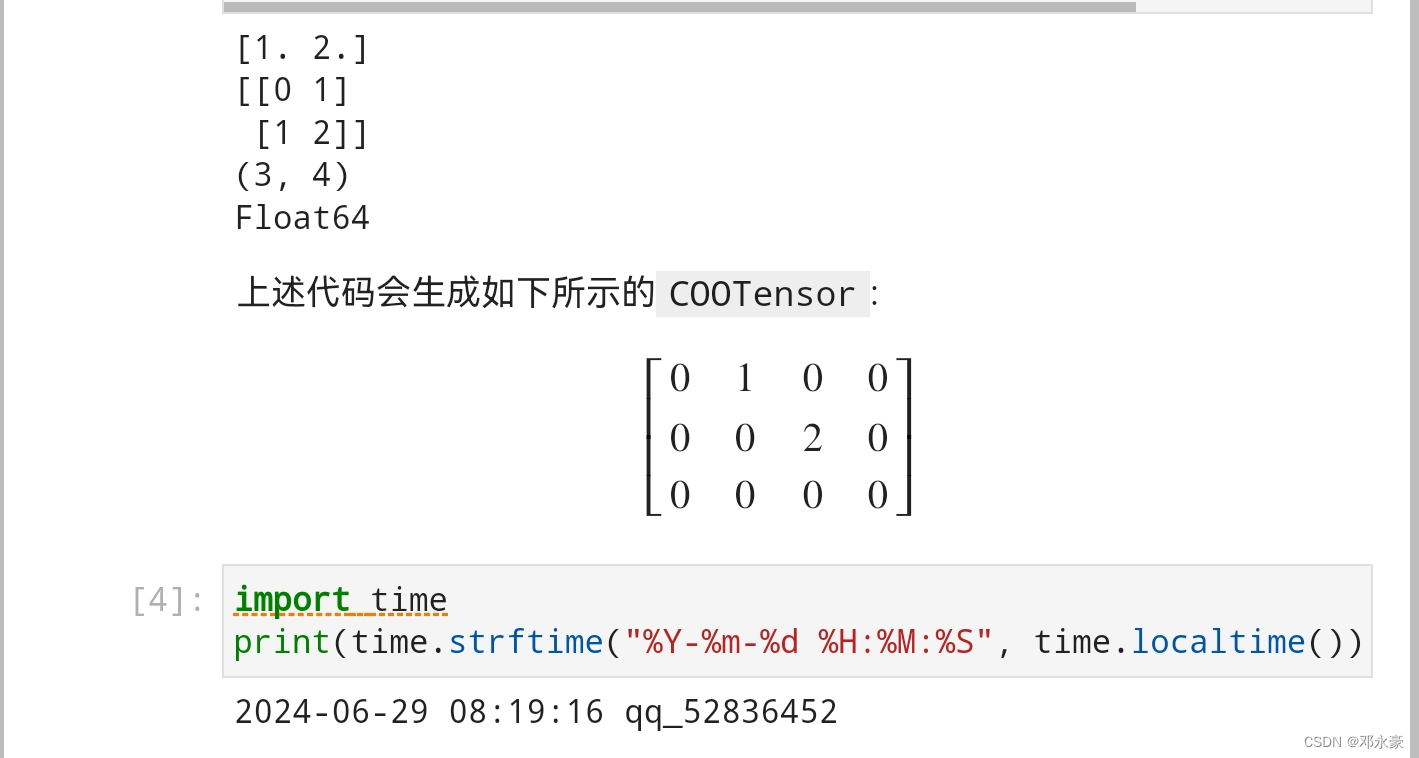
5. 稀疏张量

在本节还介绍了稀疏张量。稀疏张量是作为一种特殊的张量，它的大部分元素的值为零。稀疏张量可以减少不必要的运算、储存和通讯开销等，从而更加的高效。

以上就是今天我所学习的内容啦～