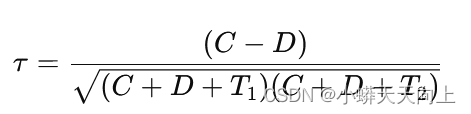计算Dice损失的函数

def Dice_loss(inputs, target, beta=1, smooth = 1e-5):
n,c, h, w = inputs.size() #
nt,ht, wt, ct = target.size() #nt,
if h != ht and w != wt:
inputs = F.interpolate(inputs, size=(ht, wt), mode="bilinear", align_corners=True)
temp_inputs = torch.softmax(inputs.transpose(1, 2).transpose(2, 3).contiguous().view(n, -1, c),-1)
temp_target = target.view(n, -1, ct)
#--------------------------------------------#
# 计算dice loss
#--------------------------------------------#
tp = torch.sum(temp_target[...,:-1] * temp_inputs, axis=[0,1])
fp = torch.sum(temp_inputs , axis=[0,1]) - tp
fn = torch.sum(temp_target[...,:-1] , axis=[0,1]) - tp
score = ((1 + beta ** 2) * tp + smooth) / ((1 + beta ** 2) * tp + beta ** 2 * fn + fp + smooth)
dice_loss = 1 - torch.mean(score)
return dice_loss
这段代码是用于计算二分类问题的混淆矩阵(Confusion Matrix)中的True Positives(TP),False Positives(FP)和False Negatives(FN)。在混淆矩阵中,TP表示模型正确预测为正类的数量,FP表示模型错误地预测为正类的数量,FN表示实际为正类但模型没有预测为正类的数量。
让我们分解这段代码来理解每个部分的作用:
-
temp_target[..., :-1] * temp_inputs:temp_target[..., :-1]获取temp_target张量中除了最后一维之外的所有元素。:-1是一个切片操作,它表示从开始到倒数第二个元素。temp_inputs是模型的预测输出。- 这两个张量进行元素相乘,只有当
temp_target的最后一维等于 1 时,才会乘以temp_inputs对应的位置的值。这模拟了只有当预测和真实标签都为正类(1)时,才认为是真正的正类检测。
-
torch.sum(..., axis=[0,1]):- 这是一个求和操作,计算在指定维度上(这里是第0维和第1维)的总和。
axis=[0,1]表示在第0维和第1维上进行求和。通常,第0维代表批量大小(batch size),第1维代表序列长度(sequence length)。- 这样做的效果是将所有正类预测的和(TP)汇总起来,无论它们在批量中的哪个位置或序列中。
-
tp = torch.sum(temp_target[...,:-1] * temp_inputs, axis=[0,1]):- 最终,
tp保存了所有正类预测的数量。
- 最终,
-
fp = torch.sum(temp_inputs, axis=[0,1]) - tp:torch.sum(temp_inputs, axis=[0,1])计算了所有预测为正类的数量,无论它们是否真的是正类。- 然后从中减去
tp,得到假正类的数量(FP),即模型错误地预测为正类的数量。
-
fn = torch.sum(temp_target[...,:-1], axis=[0,1]) - tp:torch.sum(temp_target[...,:-1], axis=[0,1])计算了实际为正类的数量,无论模型是否预测它们为正类。- 然后从中减去
tp,得到假负类的数量(FN),即实际为正类但模型没有预测为正类的数量。
综上所述,这段代码通过计算TP、FP和FN,来评估模型在二分类任务中的性能。这些值是计算精确度(Precision)、召回率(Recall)和F1得分的关键。