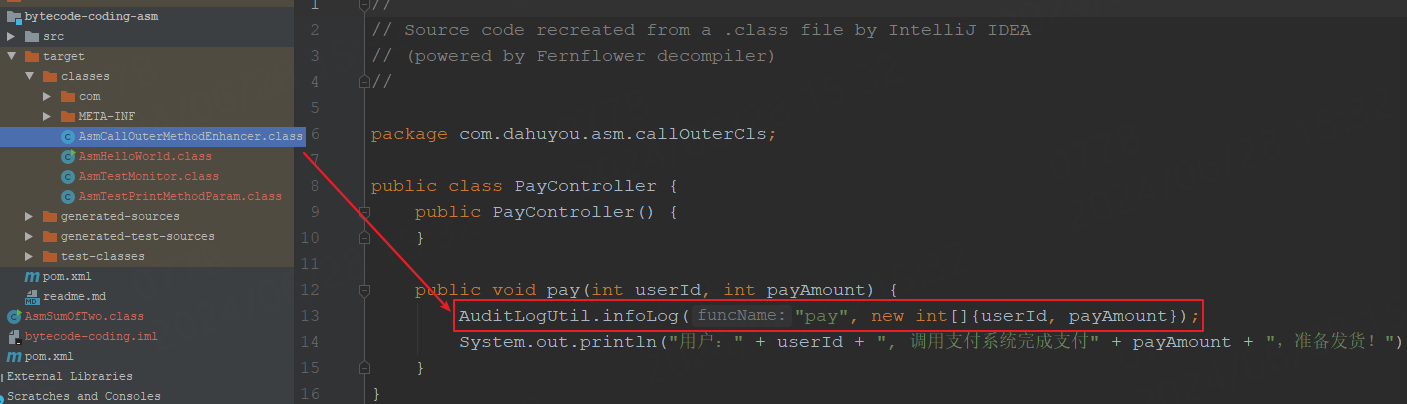
目录

一，问题 

二，思路

1，图形

 2，分析

3，伪代码 

三，代码

---

一，问题 

二，思路

1，图形

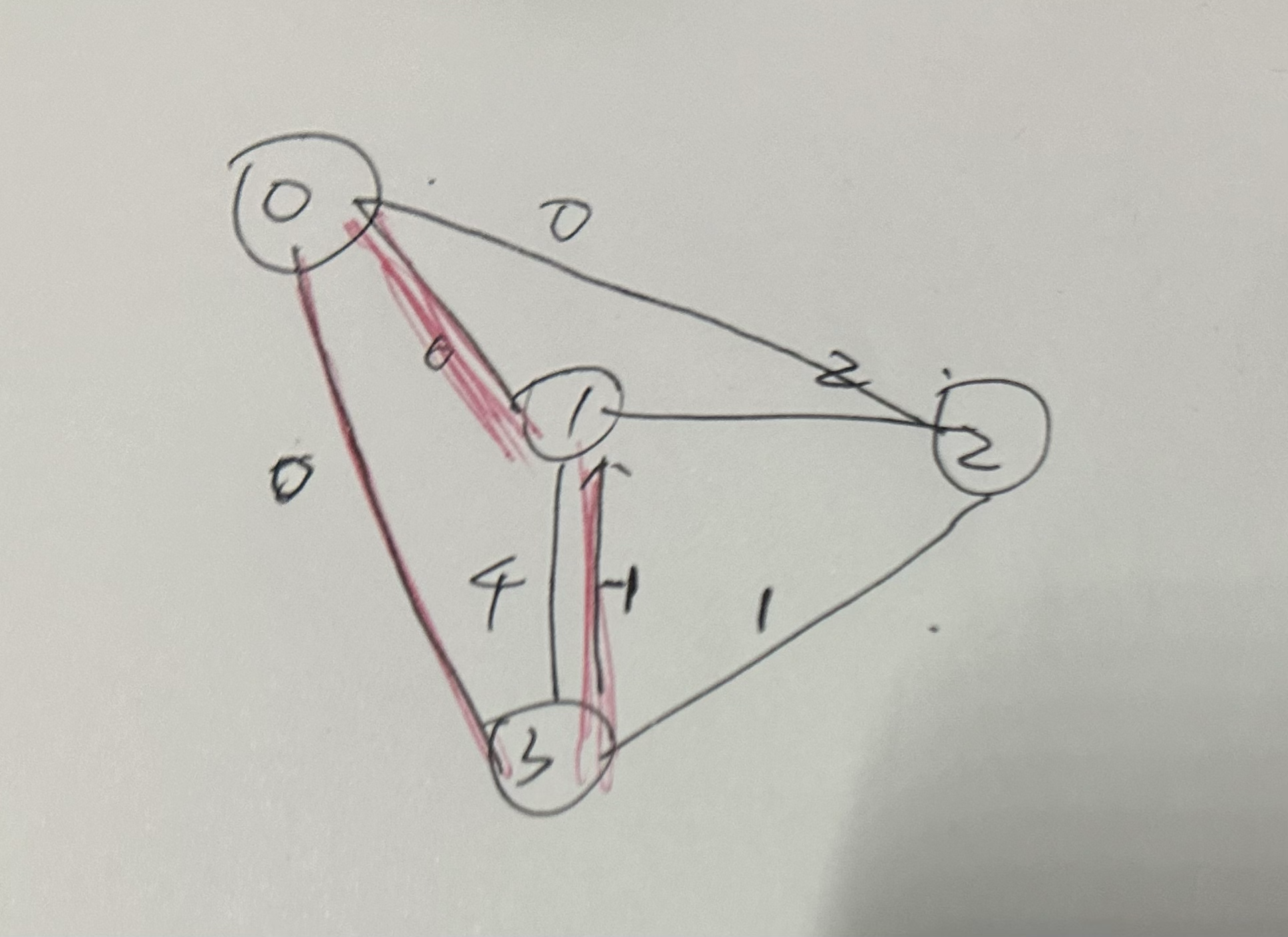
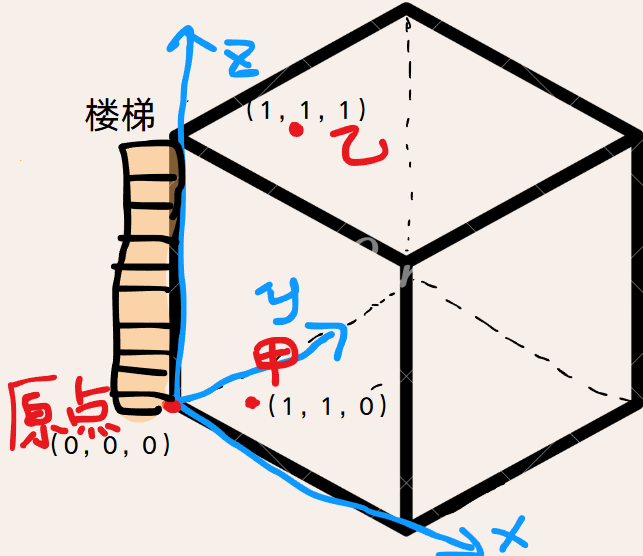
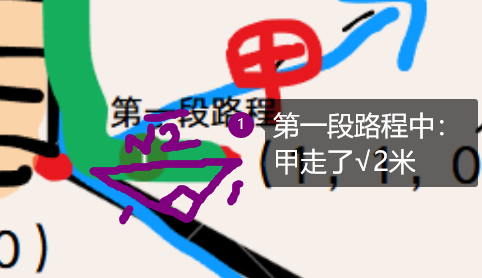
根据题目，绘制出来的图形如下👇 

 

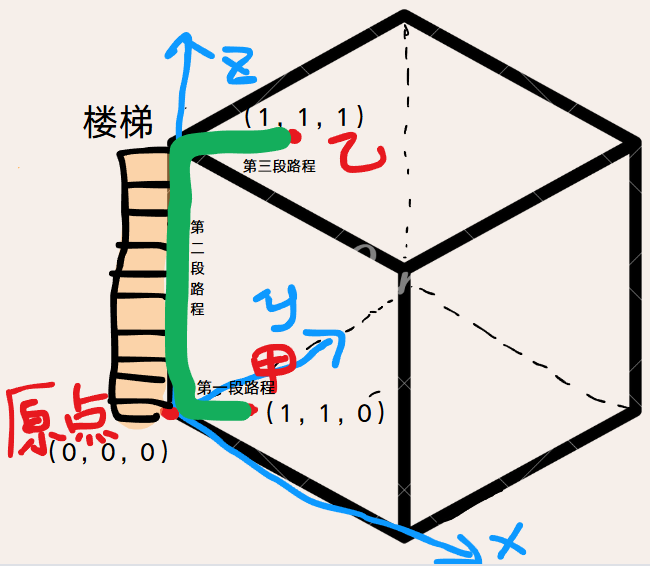
之后再绘制甲经过楼梯到已的路程（绿色的线），如下👇

 2，分析

 使用图形来进行数学分析的数学思想叫数形结合，通过上图，可以直观明了的看到，甲到已需要经过的路程：第一，第二，第三段路程。

• 第一段路程：甲还在一楼，使用勾股定理，可得甲走了√2米，如下

• 第二段路程：甲开始爬楼梯，所以甲走的路程就是楼梯的高度3
• 第三段路程：甲到了二楼，使用勾股定理，可得甲走了√2米，如下

 所以甲走到已总共走了√2+1+√2（米）

根据题目，要求甲走到已花费的时间，可以时间公式：时间等于路程除以速度。即t=s/v;

3，伪代码 

1. 声明定义六个变量g,v,x1,y1,x2,y2
2. 键盘输入六个变量的值
3. 输出时间t=(sqrt(x1*x1+y1*y1)+g+sqrt(x2*x2+y2*y2))/v

三，代码

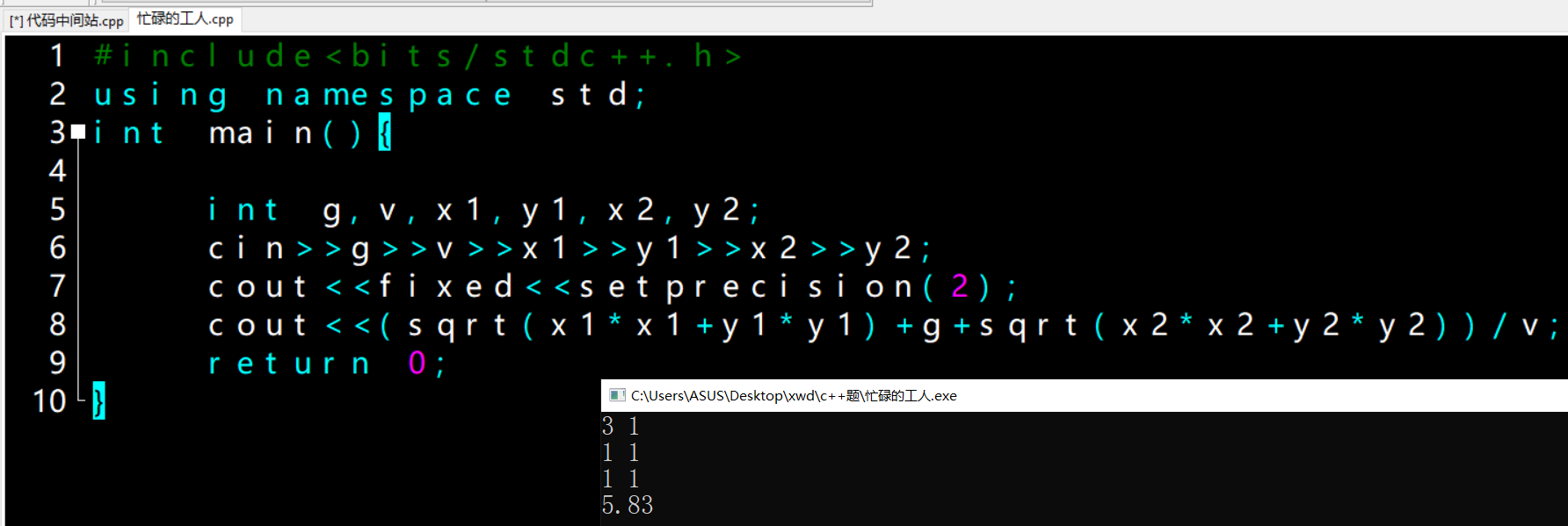
#include<bits/stdc++.h>
using namespace std;
int main(){
	
	int g,v,x1,y1,x2,y2;
	cin>>g>>v>>x1>>y1>>x2>>y2;
	cout<<fixed<<setprecision(2); 
	cout<<(sqrt(x1*x1+y1*y1)+g+sqrt(x2*x2+y2*y2))/v;
	return 0;
}

有问题请在评论区留言或者是私信我，回复时间不超过一天。