spfa的拓展应用——负环
理论
- 01分数规划
- 负环:一个环边权之和小于零
求负环的基本方法,基于SPFA:
都是基于抽屉原理,如果超过n条边,那一定有两个点相同,那就一定存在一个环
(1) 统计每个点入队次数,如果某个点入队n次,则说明存在负环;
- 本质是bellman_ford——O( n 2 n^2 n2)
(2) 统计当前每个点的最短路中所包含的边数,如果某点的最短路所包含的边数大于等于n,则说明也存在负环;
(3) 取巧做法trick:
- 当所有点入队次数超过一定阈值时, 2 n 2n 2n,则我们认为图中有很大可能是存在负环的
初始化tips
- 将起始点全部入队
- 建立虚拟原点
基本模版
int d[N];
void spfa(){
memset(d,0x3f,sizeof d);
d[1]=0;
st[1]=1;
queue<int> q;
while(q.size()){
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];~i;i=ne[i]){
int j=e[i];
if(!st[j]){
d[j]=min(d[t]+g[t][j],d[j]);
st[j]=true;
}
}
}
}
拓展模版
在基础之上增加一个cnt[N]用来判断负环
题单
1.虫洞
思考:
- “表示存在一条从田地 𝑆 走到田地 𝐸 的虫洞,走过这条虫洞,可以回到 T T T 秒之前。”回到起始点之前,这里是将时间当作边的长度,比起始的长度还小,表明存在负环
- 所以直接spfa开打
- 打完单点spfa发现并没有告诉出发点,并且是说几片农场,有些农场可能并没有连通,全部点先入队一遍吧
#include<bits/stdc++.h>
using namespace std;
int f,n,m,w;
const int N=510,M=1e4+10;
int h[N],e[M],ne[M],weight[M],idx;
int d[N],st[N],cnt[N];
void add(int a,int b,int c){
e[idx]=b,weight[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool spfa(){
memset(d,0x3f,sizeof d);
memset(st,0,sizeof st);
memset(cnt,0,sizeof cnt);
queue<int> q;
d[0]=0;
for(int i=1;i<=n;i++){
add(0,i,0);
add(i,0,0);
}
q.push(0);
while(q.size()){
int t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(d[j]>d[t]+weight[i]){
d[j]=d[t]+weight[i];
cnt[j]=cnt[t]+1;
//cout<<t<<' '<<j<<' '<<d[j]<<endl;
if(cnt[j]>=n+1){
return 1;
}
if(!st[j]){
q.push(j);
st[j]=1;
}
}
}
}
return 0;
}
signed main(){
cin>>f;
while(f--){
cin>>n>>m>>w;
memset(h,-1,sizeof h);
idx=0;
for(int i=0;i<m;i++){
int x,y,z;
cin>>x>>y>>z;
add(x,y,z),add(y,x,z);
}
for(int i=0;i<w;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,-c);
}
int res=spfa();
if(!res) puts("NO");
else puts("YES");
}
return 0;
}
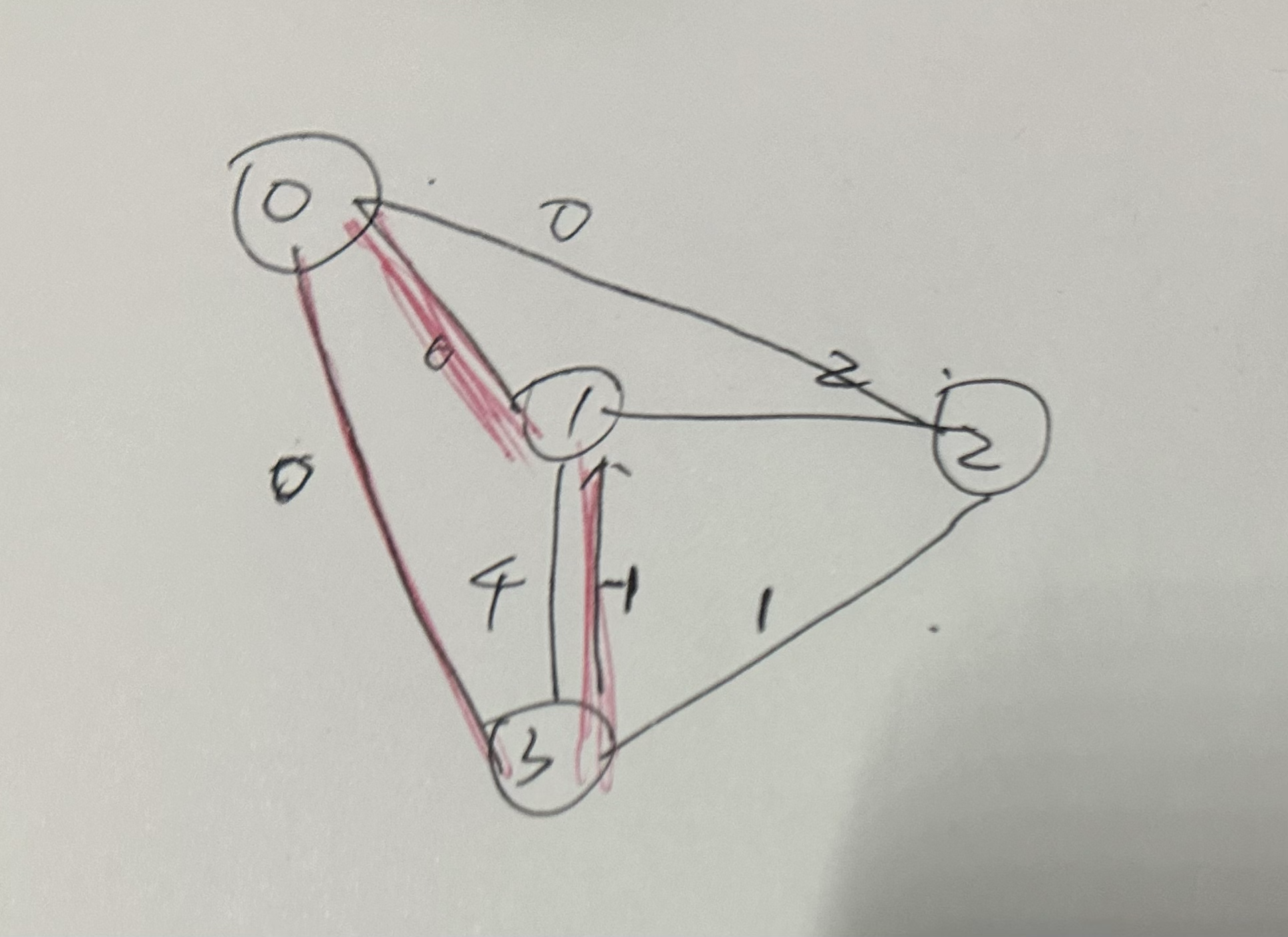
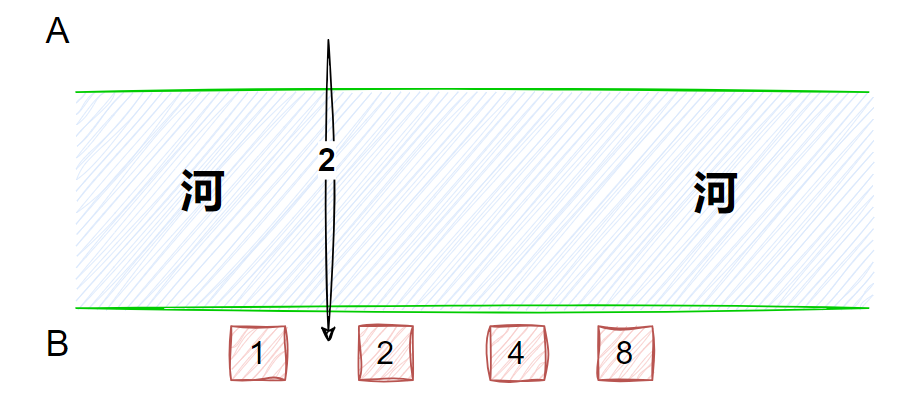
不能直接用虚拟原点建边,这样会引入多一个点,很容易出现负环,虚拟原点到其他点的变长不好定义
如图:
#include<bits/stdc++.h>
using namespace std;
int f,n,m,w;
const int N=510,M=1e4+10;
int h[N],e[M],ne[M],weight[M],idx;
int d[N],st[N],cnt[N];
void add(int a,int b,int c){
e[idx]=b,weight[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool spfa(){
memset(d,0,sizeof d);
memset(st,0,sizeof st);
memset(cnt,0,sizeof cnt);
queue<int> q;
for(int i=1;i<=n;i++){
q.push(i);
st[i]=1;
}
while(q.size()){
int t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(d[j]>d[t]+weight[i]){
d[j]=d[t]+weight[i];
cnt[j]=cnt[t]+1;
//cout<<t<<' '<<j<<' '<<d[j]<<endl;
if(cnt[j]>=n){
return 1;
}
if(!st[j]){
q.push(j);
st[j]=1;
}
}
}
}
return 0;
}
signed main(){
scanf("%d",&f);
while(f--){
cin>>n>>m>>w;
memset(h,-1,sizeof h);
idx=0;//别忘了初始化idx
for(int i=0;i<m;i++){
int x,y,z;
cin>>x>>y>>z;
add(x,y,z),add(y,x,z);
}
for(int i=0;i<w;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,-c);
}
int res=spfa();
if(!res) puts("NO");
else puts("YES");
}
return 0;
}
2. 观光奶牛
第一眼:
- “环上各点的权值之和”除以“环上各边的权值之和”第一次见
听y说:
- 01分数规划问题
思考:
- 怎么去体现最大?
- 用mid去划分,因为 ∑ ( f i ) ∑ ( w i ) \frac{\sum(f_i)}{\sum(w_i)} ∑(wi)∑(fi)有一个取值范围
- 那要怎么找到满足大于mid的环?
- 确切的说是如何找到环
- 这个mid是用来生成新的边找到正环的
- 注意”把点权放进边中“这句话在求最长路中的写法
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
int n,m;
const int N=1e3+10,M=5e3+10;
int fa[N],f[N];
int h[N],hr[N],e[M],ne[M],w[M],idx;
int cnt[N],st[N];
double d[N];
void add(int a,int b,int c){
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool check(double mid){
//其实d初不初始化都没太大关系,比较的只是相对关系,已经在
//同一层变化的相对关系是不会发生变化的
//memset(d,0,sizeof d);
memset(cnt,0,sizeof cnt);
memset(st,0,sizeof st);
int q[N];
int hh=0,tt=0;
for(int i=1;i<=n;i++){
q[tt++]=i;
st[i]=1;
}
while(hh!=tt){
int t=q[hh++];
if(hh==N) hh=0;
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(d[j]<d[t]+f[t]-mid*w[i]){
d[j]=d[t]+f[t]-mid*w[i];
cnt[j]=cnt[t]+1;
if(cnt[j]>=n) return true;
if(!st[j]){
st[j]=1;
q[tt++]=j;
if(tt==N) tt=0;
}
}
}
}
return false;
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>f[i];
memset(h,-1,sizeof h);
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
double l=1,r=1001;
while(r-l>1e-4){
double mid=(l+r)/2;
if(check(mid)) l=mid; //如果存在则说明答案在mid右边
else r=mid;
}
printf("%.2f",l);
return 0;
}
3. 单词环
第一眼:
- 不太清楚为什么和求负环有关系
- 和单词接龙会不会有关系
- 相同的处理方式:处理两个串之间的?。。。。感觉又不行
思路:
- 建图用对偶的方式,把首尾各两个字符组合成一个点,这样考虑最多情况也只有26*26种点,而边则依据字符串的长度来创建。
- 同时当mid==0时可以做一层优化
- 相当于减去零,环剩余边权之和如果仍不是正数,则说明一定没有正环
#include<bits/stdc++.h>
using namespace std;
const int N=700,M=1e5+10;
int h[N],e[M],ne[M],w[M],idx;
int n;
int st[N],cnt[N];
double d[N];
void add(int a,int b,int c){
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool check(double mid){
memset(cnt,0,sizeof cnt);
memset(st,0,sizeof st);
int q[N];
int hh=0,tt=0;
for(int i=0;i<26*26;i++){
q[tt++]=i;
st[i]=1;
}
int count=0;
while(hh!=tt){
int t=q[hh++];
if(hh==N) hh=0;
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(d[j]<d[t]+w[i]-mid){
d[j]=d[t]+w[i]-mid;
cnt[j]=cnt[t]+1;
if(cnt[j]>=N) return true;
if(++count > 10000) return true;
if(!st[j]){
q[tt++]=j;
if(tt==N) tt=0;
st[j]=1;
}
}
}
}
return false;
}
signed main(){
while(cin>>n,n){
memset(h,-1,sizeof h);
idx=0;
for(int i=0;i<n;i++){
string s;
cin>>s;
int len=s.length();
int a,b;
if(len>=2){
a=(s[0]-'a')*26+(s[1]-'a');
b=(s[len-2]-'a')*26+(s[len-1]-'a');
add(a,b,len);
}
}
if(!check(0)) puts("No solution");
else{
double l=1,r=1001;
while(r-l>1e-4){
double mid=(l+r)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%lf\n",r);
}
}
return 0;
}