题目

观测到数据：, 假定未知参数A具有先验 PDF

其中，, 是方差为的WGN，且与A独立，求A的MAP估计量。

---

解答

根据题目条件，得到条件概率：

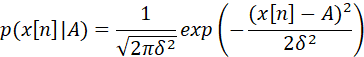
那么对于N个观察的独立数据，有：

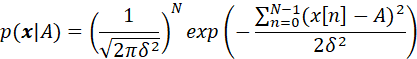
因此，得到

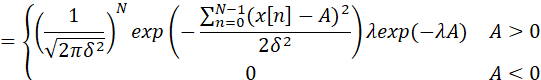
根据函数形式，和具有相同的极值点，因此对，存在：

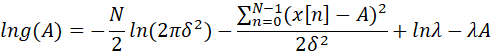
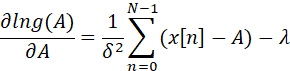
令上式等于零，得到此时A的MAP估计量为：

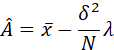
实际过程中，如果，那么可以取到MAP估计量的值，如下图所示。

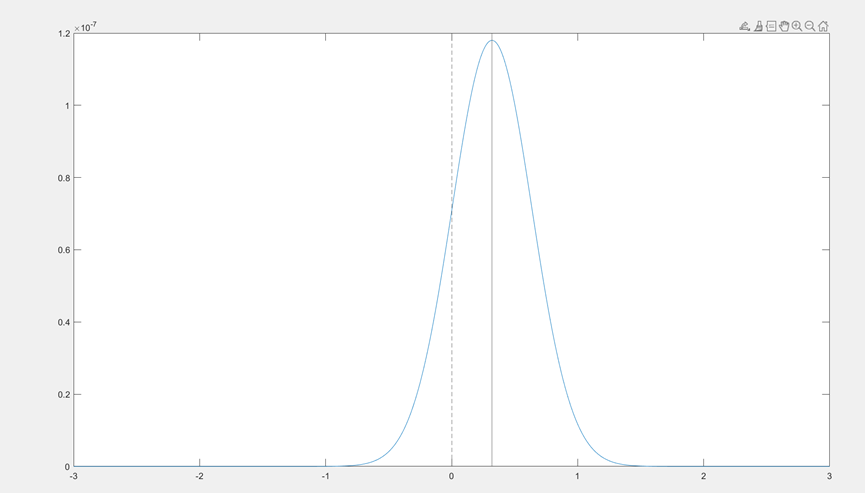
 但如，概率密度如下图。

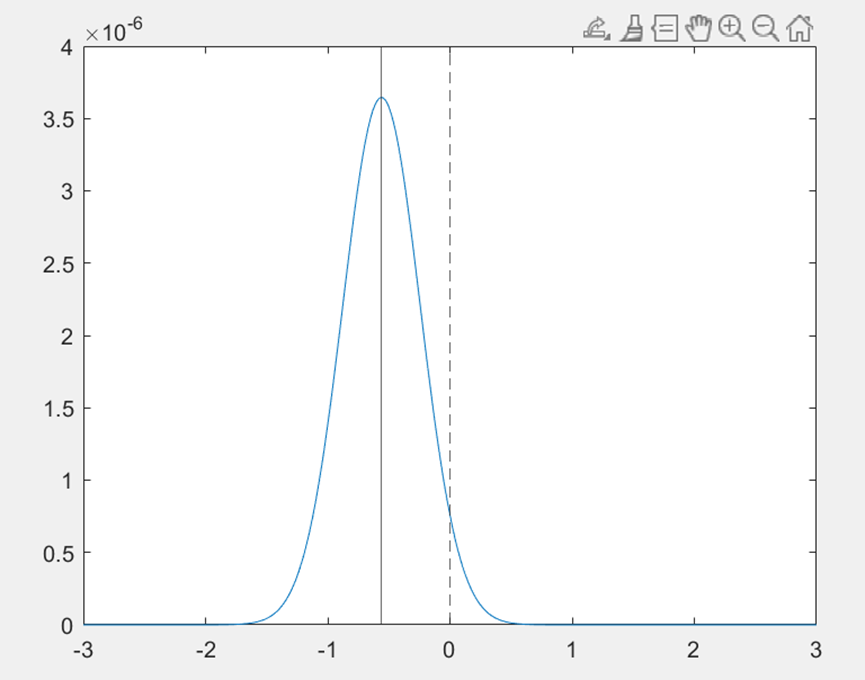
 那么概率密度只能保留的部分，此时概率密度的最大值就发生在A=0处，因此，综合来看，A的MAP估计为：

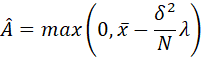
上图仿真代码：

clc, clear, close all;
N=10;
mu=0.3;
sigma=1;
x=normrnd(mu,sigma,N,1)';
lamda=1;
A_Value=-3:0.01:3;
p=zeros(1,length(A_Value));
for index=1:length(A_Value)
    A=A_Value(index);
    p(1,index)=((2*pi*sigma)^(-N/2))*exp(-1/(2*sigma)*sum((x-A).^2))*lamda.*exp(-lamda*A);
end
figure(1)
plot(A_Value,p)
hold on
xline(mean(x)-sigma*lamda/N);
xline(0,"--");
hold off