多元时间序列分析——VAR（向量自回归模型）

news2025/1/11 18:51:33

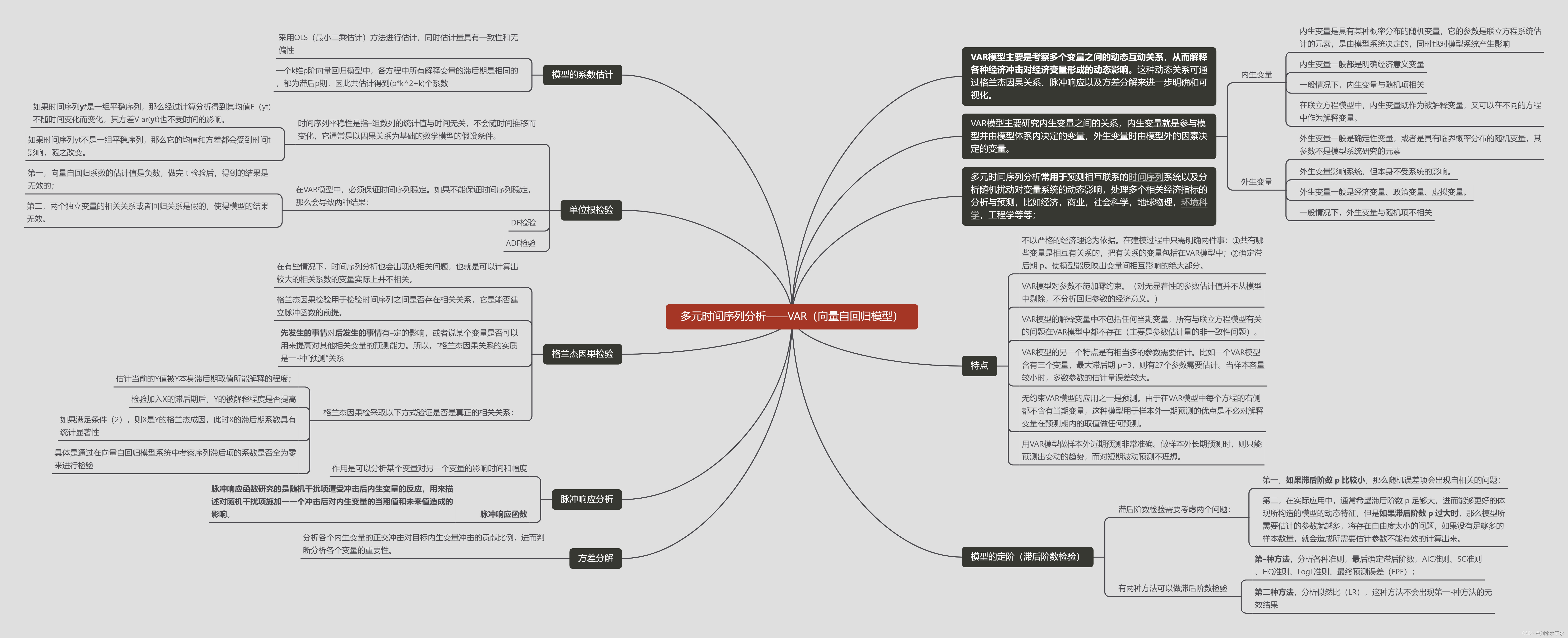
VAR模型主要是考察多个变量之间的动态互动关系，从而解释各种经济冲击对经济变量形成的动态影响。这种动态关系可通过格兰杰因果关系、脉冲响应以及方差分解来进一步明确和可视化。
VAR模型主要研究内生变量之间的关系，内生变量就是参与模型并由模型体系内决定的变量，外生变量时由模型外的因素决定的变量。
- 内生变量
  - 内生变量是具有某种概率分布的随机变量，它的参数是联立方程系统估计的元素，是由模型系统决定的，同时也对模型系统产生影响
  - 内生变量一般都是明确经济意义变量
  - 一般情况下，内生变量与随机项相关
  - 在联立方程模型中，内生变量既作为被解释变量，又可以在不同的方程中作为解释变量。
- 外生变量
  - 外生变量一般是确定性变量，或者是具有临界概率分布的随机变量，其参数不是模型系统研究的元素
  - 外生变量影响系统，但本身不受系统的影响。
  - 外生变量一般是经济变量、政策变量、虚拟变量。
  - 一般情况下，外生变量与随机项不相关
多元时间序列分析常用于预测相互联系的时间序列系统以及分析随机扰动对变量系统的动态影响，处理多个相关经济指标的分析与预测，比如经济，商业，社会科学，地球物理，环境科学，工程学等等；
特点
- 不以严格的经济理论为依据。在建模过程中只需明确两件事：①共有哪些变量是相互有关系的，把有关系的变量包括在VAR模型中；②确定滞后期 p。使模型能反映出变量间相互影响的绝大部分。
- VAR模型对参数不施加零约束。（对无显着性的参数估计值并不从模型中剔除，不分析回归参数的经济意义。）
- VAR模型的解释变量中不包括任何当期变量，所有与联立方程模型有关的问题在VAR模型中都不存在（主要是参数估计量的非一致性问题）。
- VAR模型的另一个特点是有相当多的参数需要估计。比如一个VAR模型含有三个变量，最大滞后期 p=3，则有27个参数需要估计。当样本容量较小时，多数参数的估计量误差较大。
- 无约束VAR模型的应用之一是预测。由于在VAR模型中每个方程的右侧都不含有当期变量，这种模型用于样本外一期预测的优点是不必对解释变量在预测期内的取值做任何预测。
- 用VAR模型做样本外近期预测非常准确。做样本外长期预测时，则只能预测出变动的趋势，而对短期波动预测不理想。
模型的定阶（滞后阶数检验）
- 滞后阶数检验需要考虑两个问题：
  - 第一，如果滞后阶数 p 比较小，那么随机误差项会出现自相关的问题；
  - 第二，在实际应用中，通常希望滞后阶数 p 足够大，进而能够更好的体现所构造的模型的动态特征，但是如果滞后阶数 p 过大时，那么模型所需要估计的参数就越多，将存在自由度太小的问题，如果没有足够多的样本数量，就会造成所需要估计参数不能有效的计算出来。
- 有两种方法可以做滞后阶数检验
  - 第–种方法，分析各种准则，最后确定滞后阶数，AIC准则、SC准则、HQ准则、LogL准则、最终预测误差（FPE）；
  - 第二种方法，分析似然比（LR），这种方法不会出现第一-种方法的无效结果
模型的系数估计
- 采用OLS（最小二乘估计）方法进行估计，同时估计量具有一致性和无偏性
- 一个k维p阶向量回归模型中，各方程中所有解释变量的滞后期是相同的，都为滞后p期，因此共估计得到(p*k^2+k)个系数
单位根检验
- 时间序列平稳性是指–组数列的统计值与时间无关，不会随时间推移而变化，它通常是以因果关系为基础的数学模型的假设条件。
  - 如果时间序列yt是一组平稳序列，那么经过计算分析得到其均值E（yt)不随时间变化而变化，其方差V ar(yt)也不受时间的影响。
  - 如果时间序列yt不是一组平稳序列，那么它的均值和方差都会受到时间t影响，随之改变。
- 在VAR模型中，必须保证时间序列稳定。如果不能保证时间序列稳定，那么会导致两种结果：
  - 第一，向量自回归系数的估计值是负数，做完 t 检验后，得到的结果是无效的；
  - 第二，两个独立变量的相关关系或者回归关系是假的，使得模型的结果无效。
- DF检验
- ADF检验
格兰杰因果检验
- 在有些情况下，时间序列分析也会出现伪相关问题，也就是可以计算出较大的相关系数的变量实际上并不相关。
- 格兰杰因果检验用于检验时间序列之间是否存在相关关系，它是能否建立脉冲函数的前提。
- 先发生的事情对后发生的事情有–定的影响，或者说某个变量是否可以用来提高对其他相关变量的预测能力。所以，“格兰杰因果关系的实质是一-种“预测”关系
- 格兰杰因果检采取以下方式验证是否是真正的相关关系：
  - 估计当前的Y值被Y本身滞后期取值所能解释的程度；
  - 检验加入X的滞后期后，Y的被解释程度是否提高
  - 如果满足条件（2），则X是Y的格兰杰成因，此时X的滞后期系数具有统计显著性
  - 具体是通过在向量自回归模型系统中考察序列滞后项的系数是否全为零来进行检验
脉冲响应分析
- 作用是可以分析某个变量对另一个变量的影响时间和幅度
- 脉冲响应函数
  - 脉冲响应函数研究的是随机干扰项遭受冲击后内生变量的反应，用来描述对随机干扰项施加一一个冲击后对内生变量的当期值和未来值造成的影响。
方差分解
- 分析各个内生变量的正交冲击对目标内生变量冲击的贡献比例，进而判断分析各个变量的重要性。