需要用到中序遍历

中序遍历

94. 二叉树的中序遍历 - 力扣（LeetCode）

递归

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        inoder(root,res);
        return res;
    }


    void inoder(TreeNode* root , vector<int>& res)
    {
        if(!root)
            return;
        
        inoder(root->left, res);
        res.push_back(root->val);
        inoder(root->right, res);
    }
};

迭代

一般的迭代法都是要用到栈，队列等来存root的

用栈，先进后出，中序遍历

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        
        while(root != nullptr || !stk.empty()){
            while(root)
            {
                stk.push(root);
                root = root->left;
            }

            root = stk.top();
            stk.pop();
            res.push_back(root->val);

            root = root->right;
        }

        return res;
    }
};

530. 二叉搜索树的最小绝对差 - 力扣（LeetCode）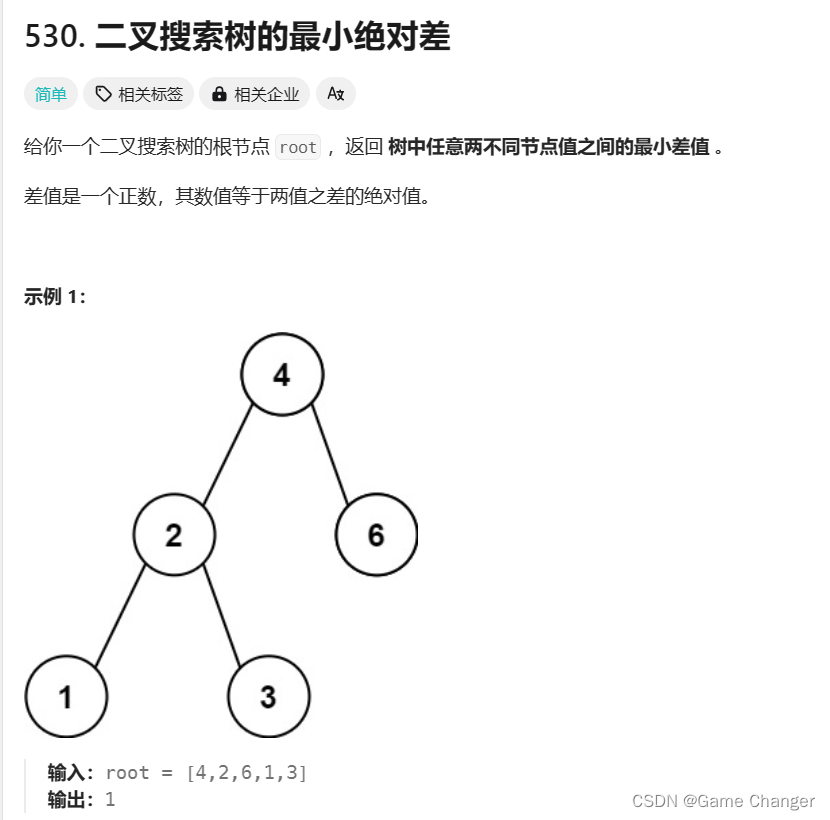

二叉搜索数的性质：二叉搜索树中序遍历得到的值序列是递增有序的

递归到最left的节点，也就是中序遍历最左边，开始ans = min(ans, root->val  - pre);

用pre来记上一个值；

INT_MAX是库里面的，表示最大的值，为了防止有比他小的；

class Solution {
public:

    void dfs(TreeNode* root, int& pre, int& ans)
    {
        if(root == nullptr)
            return;
        
        dfs(root->left, pre, ans);
        if(pre == -1){
            pre = root->val;
        }
        else{
            ans = min(ans, root->val - pre);
            pre = root->val;
        }

        dfs(root->right, pre, ans);
    }



    int getMinimumDifference(TreeNode* root) {
        int ans = INT_MAX , pre = -1;//初始化pre = -1,ans是最大值

        dfs(root, pre, ans);
        return ans;     
    }
};