- FIR数字滤波器设计(2学时)
- 要求:
- 设计一个最小阶次的低通FIR数字滤波器,性能指标为:通带0Hz~1500Hz,阻带截止频率2000Hz,通带波动不大于1%,阻带波动不大于1%,采样频率为8000Hz;
- 用一个仿真信号来验证滤波器的正确性(注意:要满足幅度要求和线性相位特性)。
- 目的:
- 利用学习到的数字信号处理知识解决实际问题;
- 了解线性相位滤波器的特殊结构;
- 要求:
实验报告:
一、实验内容
i.设计一个最小阶次的低通FIR数字滤波器,性能指标为:通带0Hz~1500Hz,阻带截止频率2000Hz,通带波动不大于1%,阻带波动不大于1%,采样频率为8000Hz;
ii.用一个仿真信号来验证滤波器的正确性(注意:要满足幅度要求和线性相位特性)。
二、实验目的
i.利用学习到的数字信号处理知识解决实际问题;
ii.了解线性相位滤波器的特殊结构;
三、涉及实验的相关情况介绍(包含使用软件或实验设备等情况)
Windows系统 Matlab 2022b
四、实验记录
1.原理基础
FIR(有限脉冲响应)滤波器是一种数字滤波器,其脉冲响应在有限的时间内衰减为零。FIR滤波器通过一系列加权系数的线性组合对输入信号进行卷积,以产生输出信号。对于低通FIR滤波器,它允许低频信号通过并抑制高频信号。
线性相位FIR滤波器具有对称或反对称的系数,这保证了滤波器在所有频率上具有相同的相位延迟,这对于避免信号失真非常重要。
设计FIR滤波器时,常用的方法有窗函数法、最小二乘法(如firls函数)和等波纹
法(如remez函数)。这些方法通过最小化通带和阻带内的误差来优化滤波器的性能。
2 实验流程
①确定滤波器参数:
包括采样频率、通带和阻带截止频率、通带和阻带波动等。
②设计FIR滤波器:
使用MATLAB的firls或remez函数设计满足性能要求的FIR滤波器。
③生成仿真信号:
创建一个包含通带和阻带频率分量的仿真信号。
④应用滤波器:
使用MATLAB的filter函数将设计的FIR滤波器应用于仿真信号。
⑤分析滤波结果:
绘制原始信号和滤波后信号的频谱图,检查通带和阻带的波动是否满足要求,并验证滤波器的线性相位特性。
3 源程序代码
%FIR 低通滤波器:1.设计低通滤波器并绘制图像 2.生成复合信号并绘制时域和频域 3.应用滤波器并绘制时域频域
%编辑人:贾雯爽
%目的:掌握模拟低通滤波器设计流程及影响参数
%最后更新时间:2024/06/05
%%1.设计低通滤波器并绘制图像
%%参数设置
fs = 8000; %设置采样频率 8k
Fp = 1500; %通带截止频率
Fs = 2000; %阻带截止频率
Rs = 0.01; %阻带衰减
Rp = 0.01; %通带波纹
figure
[n, fo, mo, w] = remezord([1500 2000], [1 0], [0.01 0.01], 8000);
b = remez(n, fo, mo, w);
%[h w] = freqz(b, 1, 128);
%plot(w/pi, abs(h));
freqz(b, 1, 128);
N=1024; %采样点数
n=0:N-1;
t=0:1/fs:1-1/fs; %时间序列
f=n*fs/N; %频率序列
%%2.生成复合信号并绘制时域和频域
Signal_Original=sin(2*pi*25*t); %信号25Hz正弦波
Signal_Noise1=sin(2*pi*2000*t); %噪声50Hz正弦波
Signal_Noise2=sin(2*pi*3000*t); %噪声100Hz正弦波
Signal_Noise3=sin(2*pi*4500*t); %噪声150Hz正弦波
Mix_Signal=Signal_Original+Signal_Noise1+Signal_Noise2+Signal_Noise3; %将信号Signal_Original和Signal_Original合成一个信号进行采样
figure
subplot(211);
plot(t, Mix_Signal); %绘制信号Mix_Signal的波形
xlabel('时间');
ylabel('幅值');
title('原始信号');
grid on;
f1 = Fs/N*(0:(N/2));
subplot(212);
y=fft(Mix_Signal, N); %对信号 Mix_Signal做FFT
P2 = abs(y/N);%取模值 根FFT公式
P1 = P2(1:N/2+1);%自变量只取前半部分
P1(2:end-1) = 2*P1(2:end-1);%单边频谱值为双边频谱值的两倍(除原点外,原点值不变)
plot(f1,P1);
xlabel('频率/Hz');
ylabel('振幅');
title('原始信号FFT');
grid on;
%%3.应用滤波器并绘制时域频域
% 绘制原始信号时域图
figure;
subplot(3,1,1);
plot(t, Mix_Signal);
title('原始信号');
xlabel('时间 (s)');
ylabel('幅度');
grid on;
%绘制滤波后时域图
Y =filter(b, 1, Mix_Signal);
subplot(3,1,2);
plot(t, Y);
title('滤波后的信号');
xlabel('时间 (s)');
ylabel('幅度');
grid on;
%绘制滤波后频域分布图
f1 = Fs/N*(0:(N/2));
subplot(313);
y=fft(Y, N);
P2_2 = abs(y/N);%取模值 根FFT公式
P1_2 = P2_2(1:N/2+1);%自变量只取前半部分
P1_2(2:end-1) = 2*P1_2(2:end-1);%单边频谱值为双边频谱值的两倍(除原点外,原点值不变)
plot(f1,P1_2,"LineWidth",1)
title("滤波后的频域分布图")
xlabel("f (Hz)")
ylabel("|P1_1(f)|")
4 实验结果
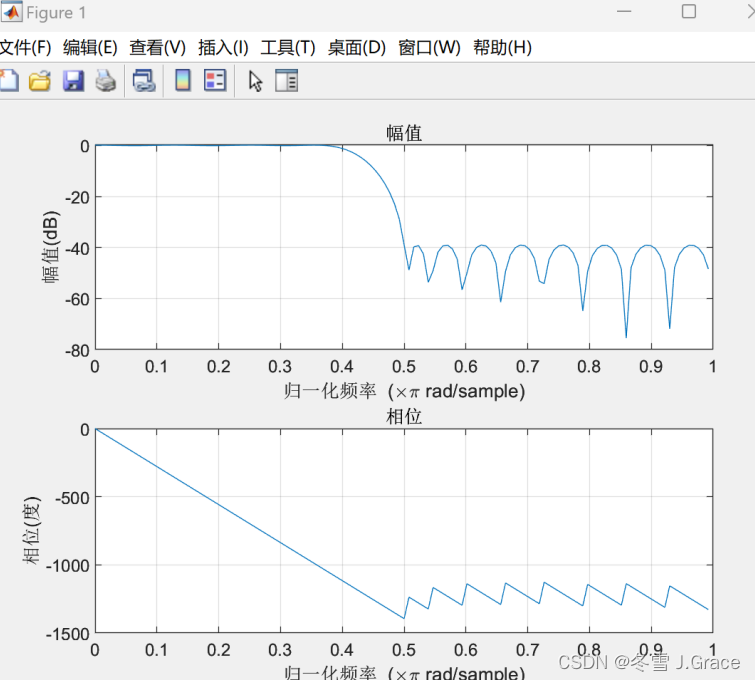
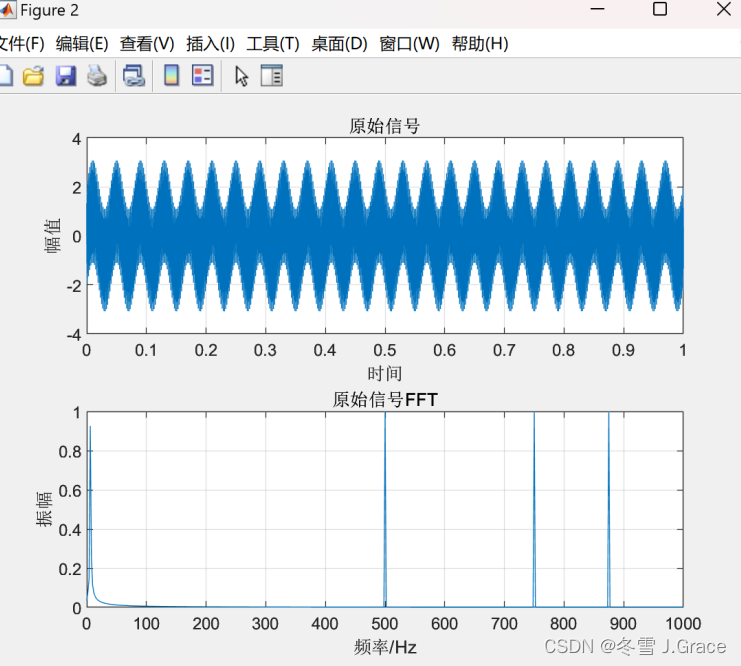
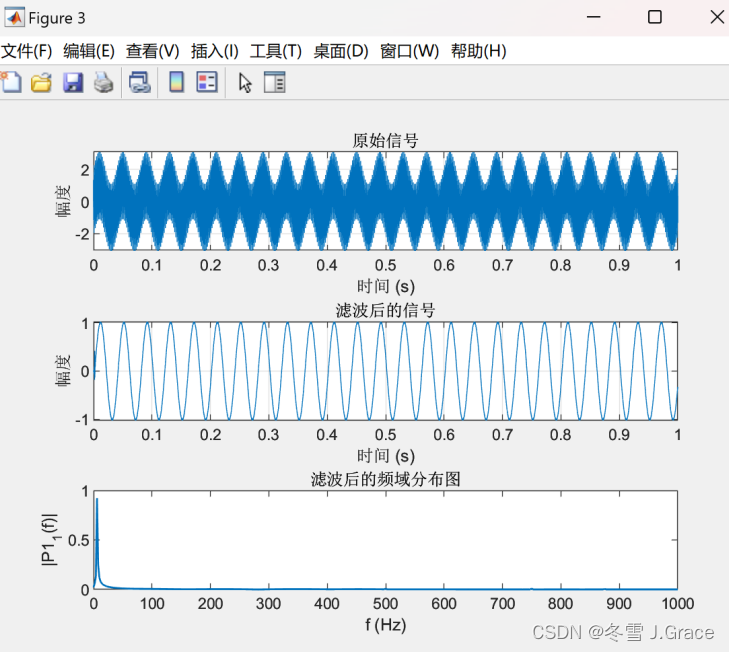
5实验结果分析
在分析实验结果时,滤波器的频率响应满足设计要求,特别是通带波动和阻带波动是否在给定的阈值内。同时,我们也验证了滤波后信号的波形或频谱如预期那样,通带内的信号得以保留,而阻带内的信号被抑制。此外,我们还验证了滤波器的线性相位特性,确保在所有频率上相位响应保持一致。
五、实验总结
通过本次实验,我们成功设计了一个满足性能指标的低通FIR数字滤波器,并通过仿真信号验证了其性能。实验结果表明,我们设计的滤波器能够有效地保留通带内的信号并抑制阻带内的信号,同时保持线性相位特性。这对于处理实际信号中的噪声和干扰具有重要意义。
然而,在实验过程中我们也发现了一些可以改进的地方。例如,滤波器的阶数对滤波性能有很大影响,我们需要通过尝试不同的阶数来找到最优解。此外,我们还可以尝试使用不同的设计方法或优化算法来进一步提高滤波器的性能。这些改进措施将为我们未来的实验和研究提供有价值的参考。
原创文章内容,学术不精恐有错漏之处,恳请各位批评指正。如有Matlab代码源文件或其他沟通需要,可通过邮箱(2642610289@qq.com)联系我,特情注意,学业繁忙难以及时回复,敬请理解。




![【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 数字排列游戏(200分) - 三语言AC题解(Python/Java/Cpp)](https://i-blog.csdnimg.cn/direct/32042c370ca64534b8347252bf707ac2.png)





![vue2(vue-cli3x[vue.config.js])使用cesium新版(1.117.0)配置过程](https://img-blog.csdnimg.cn/direct/31d9c21061bb42318efe87401fe8b3e2.png)

