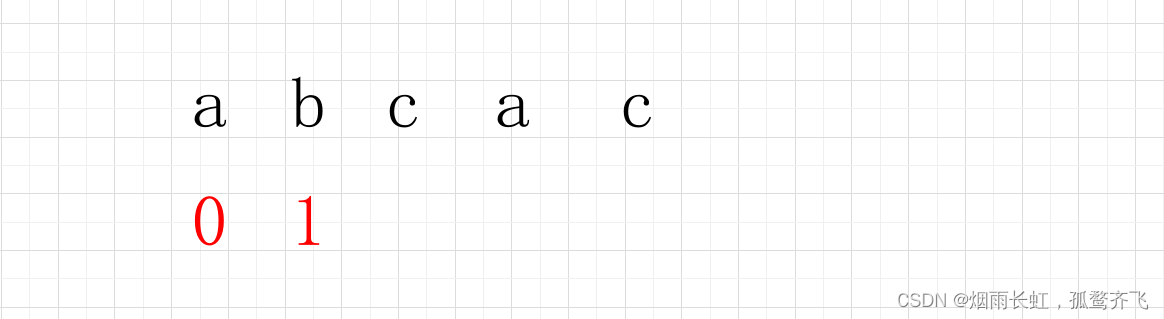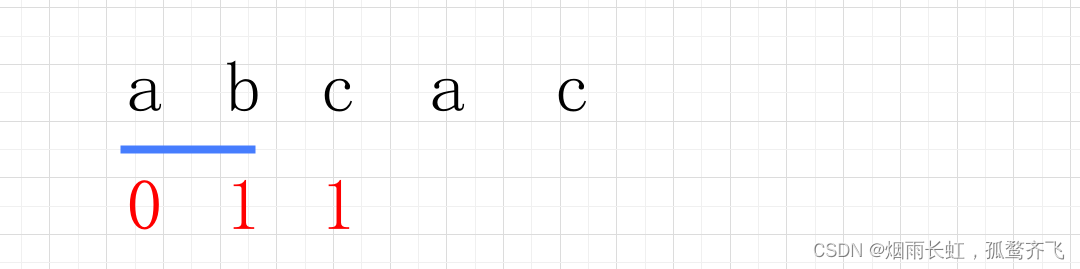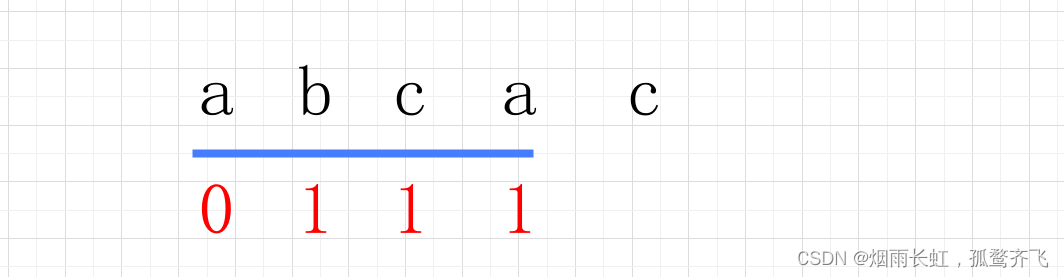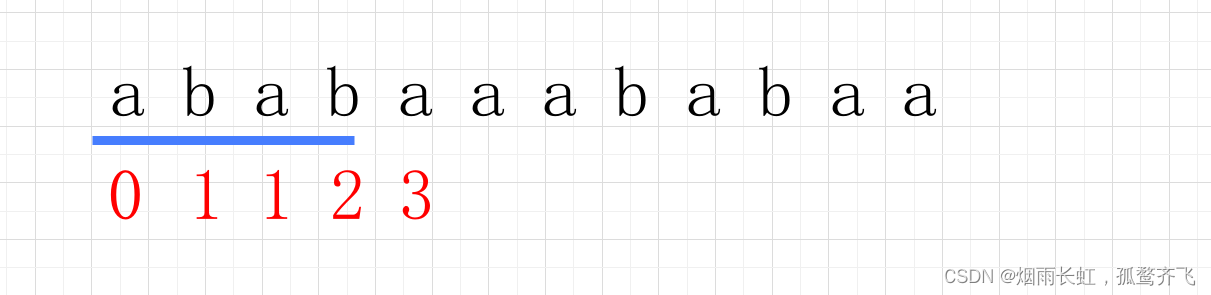竹月光中诗世界
松风影里酒生涯
目录
串的常见考法(一)BF算法
串的常见考法(二)KMP求 next数组
串的常见考法(三)串的概念及性质
串的常见考法(四)给出主串求子串数量
数组的常见考法(一)计算二维数组中的某个空间地址
数组的常见考法(二)二维数组下标的计算
数组的常见考法(三)给出表达式求个数

契子✨
承接上回,我们来复习串这一章的内容 ~
说到串,其实也不难,不过考点分布算是有点多。这里我们依旧是以题型进行分析:
<1> BF算法:一般考主串在哪个位置与子串匹配 (大概率)
<2> KMP算法:给出一个串求其 next 数组 (大概率)
<3> 串的概念以及性质(比如说特殊线性表,存储的数据元素是字符)
<4>给出一个主串求子串数量

串的大概考点便是以上这些,我们再来聊一聊数组:
考数组的话,肯定是不会给你一维数组的,要考也是考二维,常以计算一个二维数组中的某个空间地址出题
<1>计算二维数组中的某个空间地址
<2>二维数组下标的计算(可能会结合一维数组考)
<3>给出几维数组表达式求几维数组元素个数
串的常见考法(一)BF算法
StrIndex (‘DATASTRUCTURE',1,‘STR')= ()。 A. 3 B. 7 C. 5 D. 9首先我先来说明一下 StrIndex 这个函数的意思:
在主串 DATASTRUCTURE 中的第 1 个位置找到子串 STR 的位置并返回,若是找不到则返回 -1
所以这是一个字符串匹配的题目,我们只需简单的数一下从主串的第一个位置到子串的位置的距离便可以啦 ~
所以答案选择 C
S1='good',S2='morning',执行函数SubStr(S2,4,LenStr(S1))后的结果为()。 A. 'good' B. 'go' C. 'morn' D. 'ning'我先来说一下 SuStr、LenStr 的功能:
(1)substr()是 C++ 函数,主要功能是复制子字符串,要求从指定位置开始,并具有指定的长度。如果没有指定长度或超出了源字符串的长度,则子字符串将延续到源字符串的结尾
(2)strlen 是C语言的函数用来求字符串的长度
所以我们的题目应该这么理解,在 S2(morning )中的第 4 个位置复制 S1(good)长度个并存储在临时空间,S2的第 4 个位置便是 n,所以结果便是 n 开始的后面 4 个字符
所以答案选择 D
串的常见考法(二)KMP求 next数组
感觉这个有点不好讲,因为我不知道大家的基础是怎么样的,需不需要提一下 KMP 算法,算了还是提一下吧
其实做着种类型题其实不需要懂多少 KMP 的东西
只要知道最长公共前后缀怎么算就可以 KO 这道题
我现在先讲讲:
💞公共前后缀就是字符串前缀与后缀的集合中的相等部分
对于字符串 abab 来说: 前缀 [a,ab,aba],后缀 [b,ab,bab],那么公共前后缀也就是 [ab],长度为2 公共前后缀是可以重合的: [ababa]的前缀[aba]和后缀[aba]公共前后缀的长度就是3我们知道这个知识点便可以做题了
我们先来个简单点的,看下面的类型题
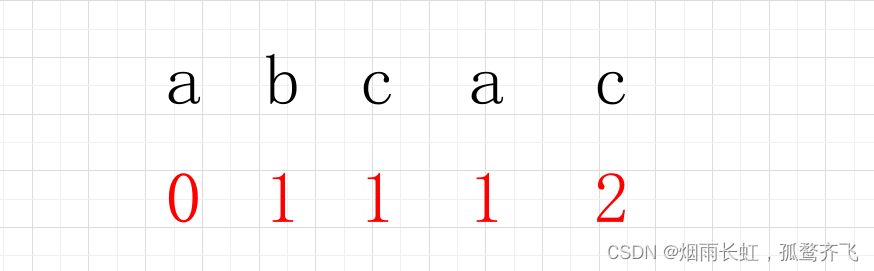
串“abcac”的next数组为( )。
我们数组的第一和第二位置直接无脑 0、1(固定的)
然后到我们的 c 位置(第三位置),就看前面那些写好 next 数组的串有没有公共前后缀
如果没有便写入 1,如果有就 1 加上最长公共前后缀的长度
我们这里看的是 ab 所以没有公共前后缀,所以写上 1 即可
这里稍微快进一下
这个时候我们来到 c 位置,我们看的便是 abca 这个串,它有公共前后缀 a 且是最大的,所以我们就要 1 加上它的长度,便是 2
是不是很简单,我们再看一道题:
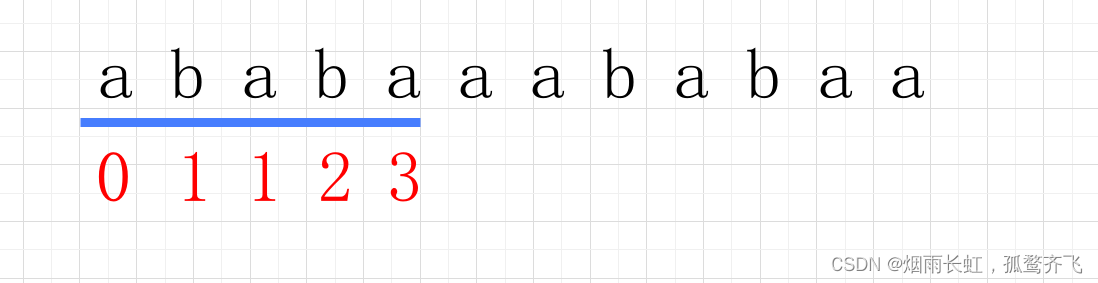
串“ababaaababaa”的next数组为() A. 012345678999 B.012121111212 C.011234223456 D.0123012322345我们还是按照之前的方法,开局无脑 01,虽然说答案都是 01,但是要一步一步来
然后开始在看看有没有公共前后缀
<1>没有直接写 1
<2>有便用 1 加上最长公共前后缀,在我们 b(第4个位置)这个地方,前面的串是 aba
那么最长公共前后缀为 1,加上便是 2
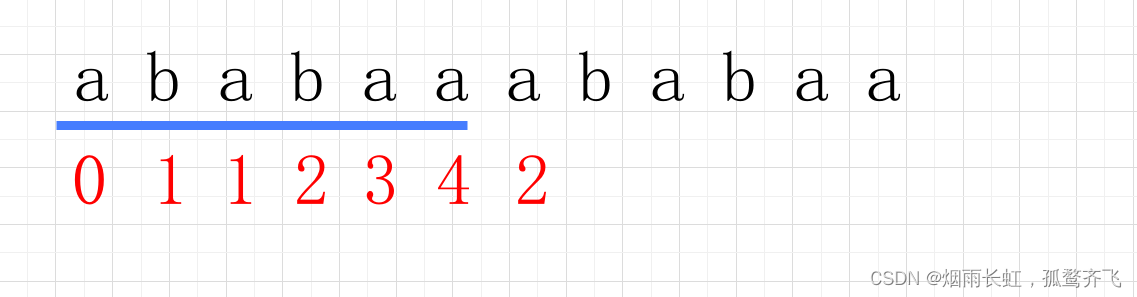
这里就不说明了,直接看图吧
这里就是我之前提到过的:公共前后缀是可以重叠的(所以这里公共前后缀是3)
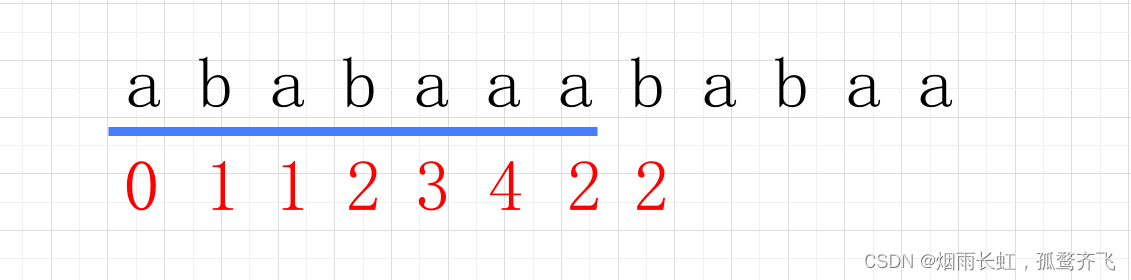
按步骤反复,便可以得出结果了:
所以答案选择 C
方法想必已经教会你们了,所以我就来讲讲别的题型啦 ~

串的常见考法(三)串的概念及性质
像这种概念题都考得很简单,我这里就直接给出答案了,放在这里只是为了让你们更好的了解题目
(1)串是一种特殊的线性表,其特殊性体现在( )。 A.可以顺序存储 B.数据元素是一个字符 C.可以链式存储 D.数据元素可以是多个字符若答案选 B
(2)串下面关于串的的叙述中,( )是不正确的? A.串是字符的有限序列 B.空串是由空格构成的串 C.模式匹配是串的一种重要运算 D.串既可以采用顺序存储,也可以采用链式存储答案选 B
串的长度是指( )。 A.串中所含不同字母的个数 B.串中所含字符的个数 C.串中所含不同字符的个数 D.串中所含非空格字符的个数答案选 B
设有两个串p和q,其中q是p的子串,求q在p中首次出现的位置的算法称为()。 A.求子串 B.联接 C.匹配 D.求串长答案选 C
如下陈述中正确的是() A.串中元素只能是字母 B.串的长度必须大于零 C.串是一种特殊的线性表 D.空串就是空白串答案选 C
串的常见考法(四)给出主串求子串数量
若串S=“software”,其子串的个数是()。 A.8 B.37 C.36 D.9大概就是像这样的题型,我们得到一个主串要求出子串的个数
这其实就是初中题好吧,不过有一点要注意的是:子串还包含空串哦
所以这就是相似的选项相差 1 的原因,就是为了坑你!
然后就是找规律了,不过不想找的话就慢慢枚举吧
首先,software 没有重复字符,长度为8 1个字符的子串有8个; 2个字符的子串有8-1个; 3个字符的子串有8-2个; ... ... 7个字符的子串有8-6个; 8个字符的子串有8-7个。 所以子串总数是1+2+3...+8=36个但是字串还包含空字串,所以我们还需要加上 1
所以这道题的答案选择 B
这里总结稍微一下规律:
字串: n(n+1)/2 + 1 非空子串:n(n+1)/2 非空真子串(不包括空串和跟自己一样的子串):n(n+1)/2 - 1

接下来为我们就来总结一下数组吧 ~ 学了那么久的程序,数组还解决不了吗?
数组的常见考法(一)计算二维数组中的某个空间地址
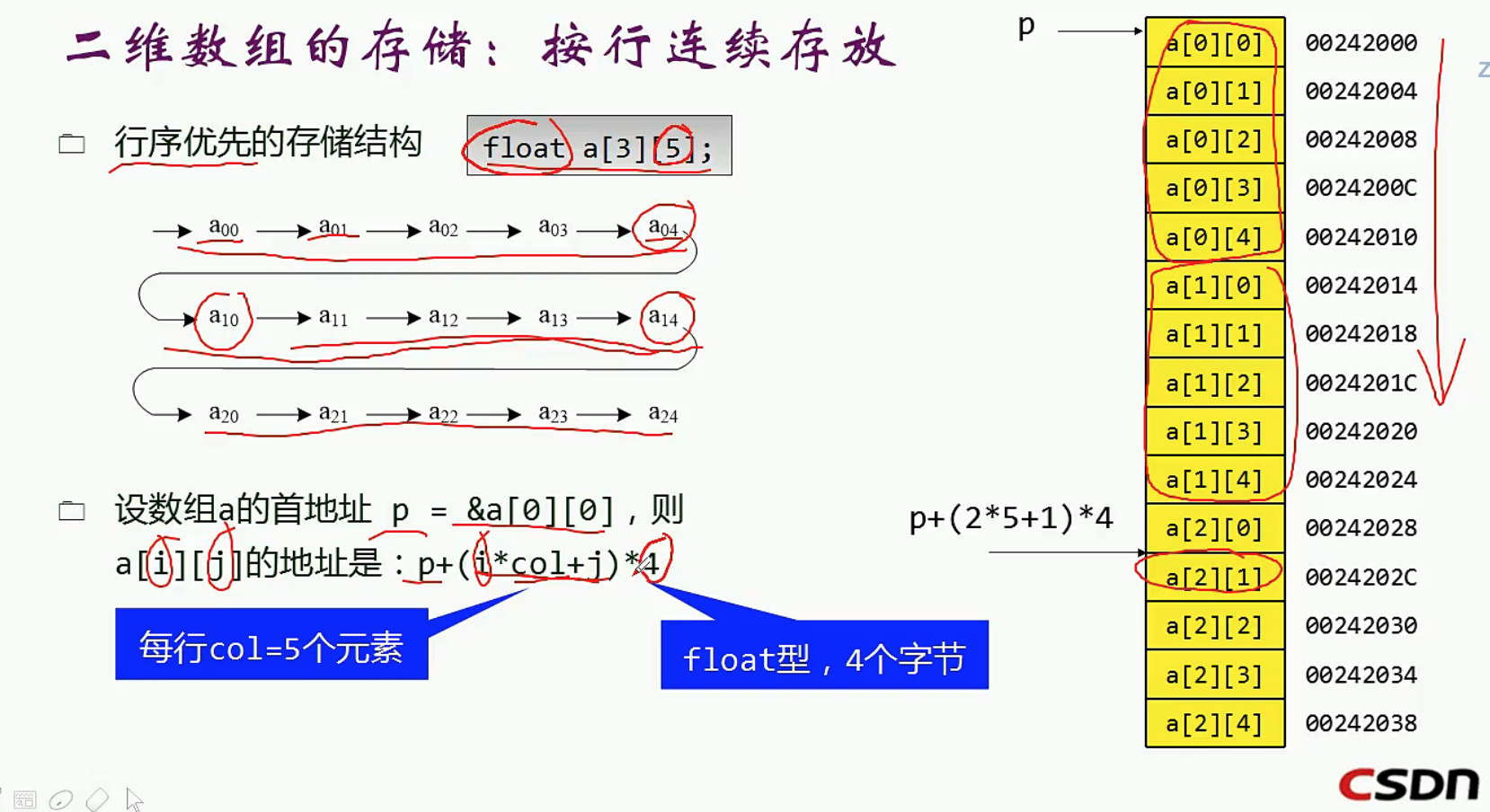
首先讲一下概念(公式)吧 ~
二维数组默认按行存储
A[i][j]的地址 = 基地址 + i * 列数 * 每个元素占的字节数 + j * 每个元素占的字节数
二维数组是 m 行 n 列,行下标和列下标都从0开始
loc[i,j] = 首地址+(i*n +j)*每个数据元素的大小
二维数组是 m 行 n 列,行下标和列下标都从1开始
loc[i,j] = 首地址+((i-1)*n +(j-1))*每个数据元素的大小二维数组默认按列存储
A[i][j]的地址 = 基地址 + i * 行数 * 每个元素占的字节数 + j * 每个元素占的字节数
二维数组是 m 行 n 列,行下标和列下标都从0开始
loc[i,j] = 首地址 + (j*m + i) * 每个数据元素的大小
二维数组是 m 行 n 列,行下标和列下标都从1开始
loc[i,j] = 首地址 + ((j-1)*m + (i-1)) * 每个数据元素的大小
假设以行序为主序存储二维数组A=array[1..100,1..100],设每个数据元素占2个存储单元,基地址为10 则LOC[5,5]=( )。 A. 808 B. 1010 C. 818 D. 1020面对这个题你有两种选择:要么记公式要么画图模拟
画图的话这里就不说了,不过是画图推出公式而已 ~
对了,有一点需要注意,如果题目没有特别说明,我们的数组都是默认从 0 开始的,这里比较特殊是从 1 开始的,我们就简单的套一下公式吧
loc[5,5] = 10 + ((5-1)*100 + (5-1)) * 2算出结果为 818
所以答案选择 C
设有一个10阶的对称矩阵A,采用压缩存储方式,以行序为主存储,a11为第一元素,其存储地址为1 每个元素占一个地址空间,则a85的地址为()。 A、13 B、33 C、18 D、40由于是对称矩阵,因此压缩存储可以认为只要存储下三角矩阵。 (1,1) 1 (2,1) (2,2) 2 (3,1) (3,2) (3,3) 3 (4,1) (4,2) (4,3) (4,4) 4 (5,1) (5,2) (5,3) (5,4) (5,5) 5 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 6 (7,1) (7,2) (7,3) (7,4) (7,5) (7,6) (7,7) 7 (8,1) (8,2) (8,3) (8,4) (8,5) 5 1+2+3+4+5+6+7+5=33首先我们得矩阵是从(1,1)开始的,因为矩阵是对称的,所以我们只需要画出一半的图形便可以直观的做出来
这里可以推一下公式:
k 代表要求的空间地址,i 表示行,j 表示列
k=(i*(i-1)/2)+j所以答案选择 B

数组的常见考法(二)二维数组下标的计算
设二维数组A[1.. m,1.. n](即m行n列)按行存储在数组B[1.. m*n]中 则二维数组元素A[i,j]在一维数组B中的下标为() A. (i-1)*n+j B. (i-1)*n+j-1 C. i*(j-1) D. j*m+i-1其实像这种题如果不会的话可以画图来理解一下的
我们的二维数组中的 22 放在一维数组中是什么地位?
放在我们一维数组来看也就是说:地位 = 上面层数 + 当前序列
设当前层数为 i,当前序列为 j
因为我们的 22 在二维数组中是在第二行的第二个位置,但是由于我们不是从 0 开始而是从 1 开始所以我们需要 (i-1),因为有 n 列所以我们需要乘以 n,即:(i-1)*n
我们的 22 在二维数组的第 2 位,所以需要 + j
模拟完了,答案自然也就出来了
所以答案选择 A
数组的常见考法(三)给出表达式求个数
数组A[0..4,-1..-3,5..7]中含有元素的个数() A. 55 B. 45 C. 36 D. 16可以看到题目给我们的是一个三位数组,但是不要慌,求个数而已,想一想我们一维二维怎么求个数的,三维就怎么求
简单来说这道题就是小学题,不过将其包装了一下
一维数组我们就想象成一条线,我们求一条线的长度不是直接去量?(看)
二维数组我们就想象成一个长方形,我们长乘宽不就成了
三维数组我们就想象成长方体,长乘宽乘高,这就是这道题的做法
我们需要找到(长、宽、高)才能算出其个数,而我们所谓的长、宽、高便是每个维的个数
每维个数 = 上限 - 下限 + 1 4-0+1=5 -1-(-3)+1=3 7-5+1=3最后:5*3*3=45 便可以求出三维数组的个数了
所以答案选择 B