目录

一、二叉树的定义

​编辑

二、二叉树的创建

三、二叉树的遍历

1、前序遍历

2、中序遍历

3、后序遍历

4、层序遍历

四、二叉树遍历方法的使用

五、二叉树的操作

1、节点的个数

2、叶子节点的个数

3、第k层节点的个数

4、二叉树的高度

5、检查值为value的元素是否存在

---

一、二叉树的定义

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分。

二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点。

---

二、二叉树的创建

二叉树每个节点有自己的元素和左右孩子节点的地址，定义一个内部类来定义每个节点。

public class BinaryTree {


    static class TreeNode{

        public char val;

        public TreeNode left;

        public TreeNode right;


        public TreeNode(char val) {

            this.val = val;

        }

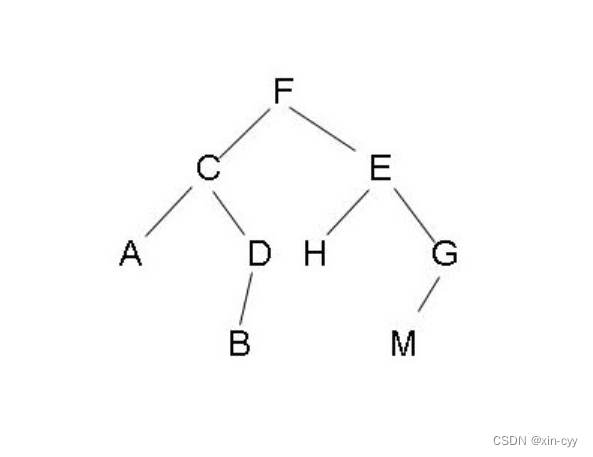
        public TreeNode creatTree(){

            TreeNode A=new TreeNode('A');

            TreeNode B=new TreeNode('B');

            TreeNode C=new TreeNode('C');

            TreeNode D=new TreeNode('D');

            TreeNode E=new TreeNode('E');

            TreeNode F=new TreeNode('F');

            TreeNode G=new TreeNode('G');

            TreeNode H=new TreeNode('H');


            A.left=B;

            A.right=C;

            B.left=D;

            B.right=E;

            C.left=F;

            C.right=G;

            E.right=H;


            return A;

        }

    }

---

三、二叉树的遍历

1、前序遍历

前序遍历：根-->根的左子树-->根的右子树

 void preorder(TreeNode root){

        if (root==null){

            return;

        }

        System.out.print(root.val+" ");


        preorder(root.left);

        preorder(root.right);

    }

---

2、中序遍历

中序遍历：根的左子树-->根-->根的右子树

void inorder(TreeNode root){

        if (root==null){

            return;

        }

        preorder(root.left);

        System.out.print(root.val);

        preorder(root.right);

    }

---

3、后序遍历

后序遍历：根的左子树-->根的右子树-->根

void postorder(TreeNode root){

            if (root==null){

                return;

            }

            postorder(root.left);

            postorder(root.right);

            System.out.print(root.val);

    }

---

4、层序遍历

将节点的值放入队列中，然后出队列。

 void levelorder(TreeNode root){

            if (root==null){

                return;

            }

        Queue<TreeNode>queue=new LinkedList<>();

            queue.offer(root);

            while (!queue.isEmpty()){

                TreeNode cur=queue.poll();

                System.out.print(cur.val+" ");

                
                if (cur.left!=null){

                    queue.offer(cur.left);

                }

                if (cur.right!=null){

                    queue.offer(cur.right);

                }

            }

    }

---

四、二叉树遍历方法的使用

定义一个Main方法

public class Main {

    public static void main(String[] args) {

        BinaryTree binaryTree=new BinaryTree();

        BinaryTree.TreeNode root=binaryTree.creatTree();


        //前序遍历

        binaryTree.preorder(root);
        System.out.println();


        //中序遍历
        binaryTree.inorder(root);
        System.out.println();


        //后序遍历
        binaryTree.postorder(root);
        System.out.println();


        //层序遍历
        binaryTree.levelorder(root);
        System.out.println();

    }

}

执行结果：

A B D E H C F G 
D B E H A F C G 
D H E B F G C A 
A B C D E F G H

---

五、二叉树的操作

1、节点的个数

遍历求节点个数

 public int usedSize;

    int getSize(TreeNode root){

        if (root==null){

            return 0;

        }

        usedSize++;

        getSize(root.left);

        getSize(root.right);

        return usedSize;

    }

---

子问题求节点个数

  int getSize1(TreeNode root){

        if (root==null){

            return 0;

        }

        return getSize1(root.left)+getSize1(root.right)+1;

    }

---

2、叶子节点的个数

当节点的左右子节点为空时，则该节点就是叶子节点。

遍历求叶子节点

 public int leafSize;

    int getLeafNodeCount(TreeNode root) {

        if (root == null) {

            return 0;

        }

        if (root.left == null && root.right == null) {

            leafSize++;

        }

            getLeafNodeCount(root.left);

            getLeafNodeCount(root.right);

            return leafSize;

        }

---

子问题求叶子节点

int getLeafNodeCount1(TreeNode root){

        if (root==null){

            return 0;

        }

        if (root.left==null&&root.right==null){

            return 1;

        }

        return getLeafNodeCount1(root.left)+getLeafNodeCount1(root.right);

        }

---

3、第k层节点的个数

 int getKUsedSize(TreeNode root,int k){

        if (root==null){

            return 0;

        }

        if (k==1){

            return 1;

        }

        return getKUsedSize(root.left,k-1)+getKUsedSize(root.right,k-1);

    }

---

4、二叉树的高度

 int getHight(TreeNode root){

        if (root==null){

            return 0;

        }

        int getleftHight=getHight(root.left);

        int getrightHight=getHight(root.right);


        return getleftHight > getrightHight ? getleftHight+1 : getrightHight+1;

    }

---

5、检查值为value的元素是否存在

 TreeNode findValue(TreeNode root,char value){

        if (root==null){

            return null;

        }

        if (root.val==value){

            return root;

        }

        TreeNode ret1=findValue(root.left,value);

        if (ret1!=null){

            return ret1;

        }

        TreeNode ret2=findValue(root.right,value);

        if (ret2!=null){

            return ret2;

        }

        return null;

    }

---