🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础
💫个人格言: "如无必要,勿增实体"

文章目录
- 高斯混合模型(Gaussian Mixture Models, GMM)深度解析
- 引言
- 1. GMM基础
- 1.1 概念介绍
- 1.2 模型表示
- 2. 参数估计:期望最大化(EM)算法
- 2.1 EM算法概述
- 2.2 具体步骤
- 3. GMM的应用
- 3.1 数据聚类
- 3.2 密度估计
- 3.3 语音识别与图像分割
- 4. GMM的挑战与改进
- 4.1 参数选择与过拟合
- 4.2 算法收敛性与初始化
- 4.3 模型扩展
- 5. 结语
高斯混合模型(Gaussian Mixture Models, GMM)深度解析

引言
在机器学习与统计学领域,高斯混合模型(GMMs)是一种强大的非监督学习工具,广泛应用于数据聚类、密度估计及隐含变量建模。GMM通过结合多个高斯分布(正态分布),为数据点的分布提供了一种灵活且适应性强的描述方式。本文将系统地介绍GMM的基本概念、数学原理、算法流程、参数估计方法、优缺点以及实际应用场景,旨在为读者提供一个全面而深入的理解。
1. GMM基础
1.1 概念介绍
高斯混合模型是一种概率模型,它假设数据是由K个不同的高斯分布(也称作组件)混合而成。每个高斯分布代表数据的一个潜在类别或簇,而数据点属于某个类别的概率决定了它由哪个高斯分布产生。
1.2 模型表示
设有一个观测数据集X = {x_1, x_2, ..., x_n},每个数据点x_i是D维的。GMM模型可以用以下形式表示:
p ( x ∣ θ ) = ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) p(x|\theta) = \sum_{k=1}^{K}\pi_k \mathcal{N}(x|\mu_k, \Sigma_k) p(x∣θ)=k=1∑KπkN(x∣μk,Σk)
其中, p i k pi_k pik是第k个高斯成分的先验概率(或混合比例),满足 s u m k = 1 K π k = 1 sum_{k=1}^{K}\pi_k = 1 sumk=1Kπk=1; ( N ( x ∣ μ k , Σ k ) (\mathcal{N}(x|\mu_k, \Sigma_k) (N(x∣μk,Σk)表示多维高斯分布,其中 μ k \mu_k μk是该分布的均值向量, Σ k \Sigma_k Σk是协方差矩阵; θ = { π k , μ k , Σ k } k = 1 K \theta = \{\pi_k, \mu_k, \Sigma_k\}_{k=1}^{K} θ={πk,μk,Σk}k=1K是GMM的全体参数。
2. 参数估计:期望最大化(EM)算法

2.1 EM算法概述
由于GMM直接求解参数 θ \theta θ非常困难,通常采用期望最大化(Expectation-Maximization, EM)算法来迭代估计这些参数。EM算法分为两步:
- E步骤(Expectation):计算给定当前参数下,每个数据点属于每个高斯分量的后验概率(责任权重)。
- M步骤(Maximization):基于E步骤得到的责任权重,重新估计参数 θ \theta θ,以最大化完全数据的对数似然函数。
2.2 具体步骤
- 初始化:随机或启发式地选择初始参数值 θ ( 0 ) \theta^{(0)} θ(0)。
- 迭代:
- E步骤:计算每个数据点
x_i对于每个高斯分量的归属概率(或责任)r_{ik}。
r i k = π k N ( x i ∣ μ k , Σ k ) ∑ j = 1 K π j N ( x i ∣ μ j , Σ j ) r_{ik} = \frac{\pi_k \mathcal{N}(x_i|\mu_k, \Sigma_k)}{\sum_{j=1}^{K}\pi_j \mathcal{N}(x_i|\mu_j, \Sigma_j)} rik=∑j=1KπjN(xi∣μj,Σj)πkN(xi∣μk,Σk) - M步骤:基于
r_{ik},更新模型参数:
π k ( t + 1 ) = 1 n ∑ i = 1 n r i k ( t ) μ k ( t + 1 ) = ∑ i = 1 n r i k ( t ) x i ∑ i = 1 n r i k ( t ) Σ k ( t + 1 ) = ∑ i = 1 n r i k ( t ) ( x i − μ k ( t + 1 ) ) T ( x i − μ k ( t + 1 ) ) ∑ i = 1 n r i k ( t ) \pi_k^{(t+1)} = \frac{1}{n}\sum_{i=1}^{n}r_{ik}^{(t)} \mu_k^{(t+1)} = \frac{\sum_{i=1}^{n}r_{ik}^{(t)}x_i}{\sum_{i=1}^{n}r_{ik}^{(t)}} \Sigma_k^{(t+1)} = \frac{\sum_{i=1}^{n}r_{ik}^{(t)}(x_i - \mu_k^{(t+1)})^T(x_i - \mu_k^{(t+1)})}{\sum_{i=1}^{n}r_{ik}^{(t)}} πk(t+1)=n1i=1∑nrik(t)μk(t+1)=∑i=1nrik(t)∑i=1nrik(t)xiΣk(t+1)=∑i=1nrik(t)∑i=1nrik(t)(xi−μk(t+1))T(xi−μk(t+1))
- E步骤:计算每个数据点
- 收敛判断:当参数变化小于某一阈值或达到最大迭代次数时,停止迭代。
3. GMM的应用
3.1 数据聚类
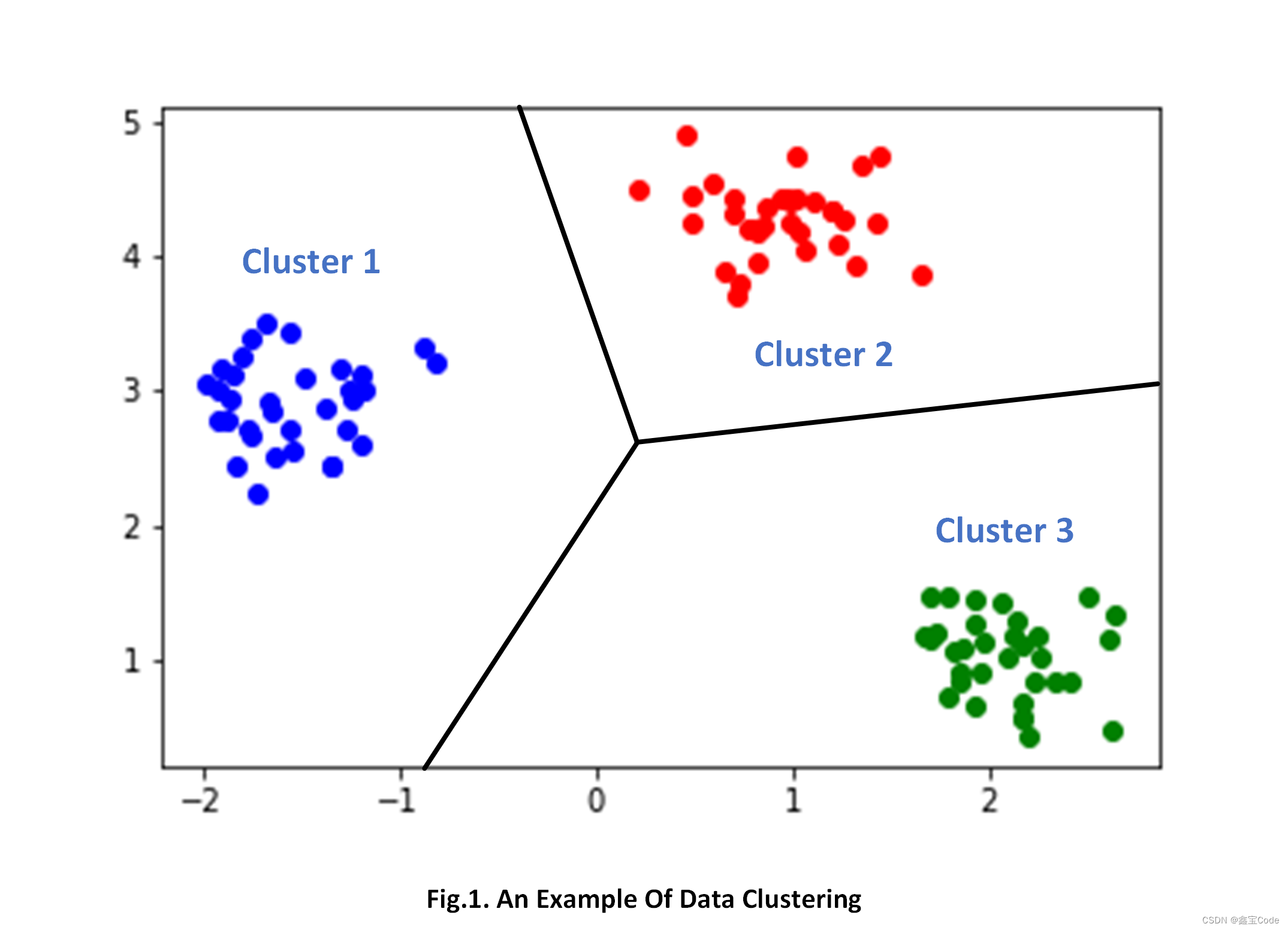
GMM不仅能够估计数据的分布情况,还能自然地进行数据聚类。通过找到数据点最可能属于的高斯分量,即可实现软聚类(每个点可以属于多个簇,以概率表示)。
3.2 密度估计
GMM能够提供一个连续的概率密度函数来描述数据分布,适用于复杂的、多模态的数据密度估计。
3.3 语音识别与图像分割
在信号处理和计算机视觉领域,GMM常用于特征提取和分类,如语音信号的声学建模和图像区域的分割。
4. GMM的挑战与改进
4.1 参数选择与过拟合
选择合适的K值(高斯分量的数量)至关重要,过小会导致模型无法捕获数据的复杂性,过大则可能过拟合。交叉验证是常用的解决方案。
4.2 算法收敛性与初始化
EM算法可能因初始化不佳而陷入局部最优。多种初始化策略(如K-means++)和多次随机初始化结合选择最佳解可以改善这一问题。
4.3 模型扩展
为了处理特定问题,GMM可以与其他模型结合,如隐马尔可夫模型(HMM)、Dirichlet过程GMM等,以适应更复杂的数据结构和动态特性。
5. 结语
高斯混合模型以其强大的灵活性和适应性,在数据挖掘、机器学习和统计分析等领域发挥着重要作用。尽管面临参数选择和收敛性等挑战,通过不断的技术创新和算法优化,GMM的应用潜力仍在不断拓展。无论是学术研究还是工业应用,掌握GMM的原理和实践都是提升数据分析能力的关键一步。随着计算能力的增强和算法理论的深化,期待GMM在未来能解锁更多领域的可能性。