【力扣高频题】011. 盛最多水的容器

news2024/7/7 17:39:05

前面的算法文章，更新了许多 专题系列 。包括：滑动窗口、动态规划、加强堆、二叉树递归套路 等。

还没读过的小伙伴可以关注一下，在主页中点击对应链接查看哦~

接下来的一段时间，将持续 「力扣高频题」 系列文章，想刷 力扣高频题 的小伙伴也可以关注一波哦 ~

言归正传，今天我们来讲一道中等难度的力扣高频题，与 接雨水问题 很类似哦~

11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的 最大水量 。

示例 1：

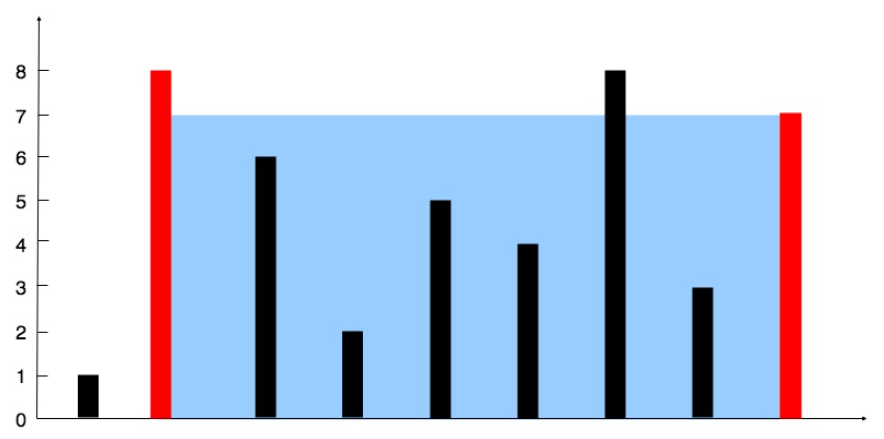
输入： [1,8,6,2,5,4,8,3,7]

输出： 49

解释： 图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7] 。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49 。

示例 2：

输入： [1,1]

输出： 1

提示：
n == height.length
2 <= n <= $10^5$
0 <= height[i] <= $10^4$

思路分析

一个很简单的道理：能够装多少水量，取决于较短的竖线的长度，以及两根竖线之间的距离。

总水量 = 较短的长度（高度） × 距离（宽度）

由于两个因素变量是相乘的关系，两者的改变可能会导致结果呈现此起彼伏的变化，不便于讨论分析。因此，需要想办法控制变量。

显然，若 高度一样 的情况下，距离越长 能够存储的 最大水量越大 。最终要找的就是最大值，因此设置两个指针一开始先分别指向数组的首尾（此时距离最长），然后逐步缩小该距离（即移动双指针）。

要想当 距离缩短 时，反而获得更大的存储水量，唯一的办法就是 增高较短边的长度 。

思考到这里，做题的思路就逐步清晰了：缩短距离时，优先要移动此时较短的指针，只有这样才能有增大最终答案的 可能性 。

如果错误的先移动了较长的边，高度只有可能 不变或减小 ，距离 一定会减小，导致了最终答案也一定是变小，做了无用功。

代码

public static int maxArea(int[] h) {
    int max = 0;
    int l = 0;
    int r = h.length - 1;
    while (l < r) {
        max = Math.max(max, Math.min(h[l], h[r]) * (r - l));
        if (h[l] > h[r]) {
            r--;
        } else {
            l++;
        }
    }
    return max;
}