傅里叶变换，拉普拉斯变换，卷积 & 卷积定理

开胃小菜（收敛性）

傅里叶变换是一种将时间域信号转换为频率域信号的数学变换，它能够揭示信号的频率成分。
拉普拉斯变换是傅里叶变换的一种推广形式，用于线性常微分方程的求解。
卷积是一种积分运算，常用于信号处理中，表示一个信号对另一个信号的响应。
卷积定理指出，两个信号的卷积在时间域等价于它们在频域的乘积。

收敛性定义
狄利赫利条件：

1、 𝑓(𝑥) 绝对可积，即

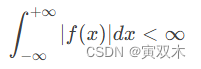
2、在任何有限区间内， 𝑓(𝑥) 只有有限个最大值和最小值。
3、在任何有限区间内， 𝑓(𝑥) 有有限个不连续点，并且在每个不连续点都必须是有限值。

---

一、傅里叶变换

​傅里叶变换（Fourier Transform）是一种将一个时间域信号转换为其频域表示的方法，它能够将信号分解成不同的频率成分。
傅里叶逆变换（Inverse Fourier Transform）则是将频域表示的信号重新转换回时间域的过程。
傅里叶变换和其逆变换在信号处理、图像处理、通信、物理学等领域有着广泛的应用。

核心原理

连续周期信号可以表示为一系列不同频率的正弦波的线性叠加
连续周期信号可以表示为一系列不同频率的正弦波的线性叠加
连续周期信号可以表示为一系列不同频率的正弦波的线性叠加

---

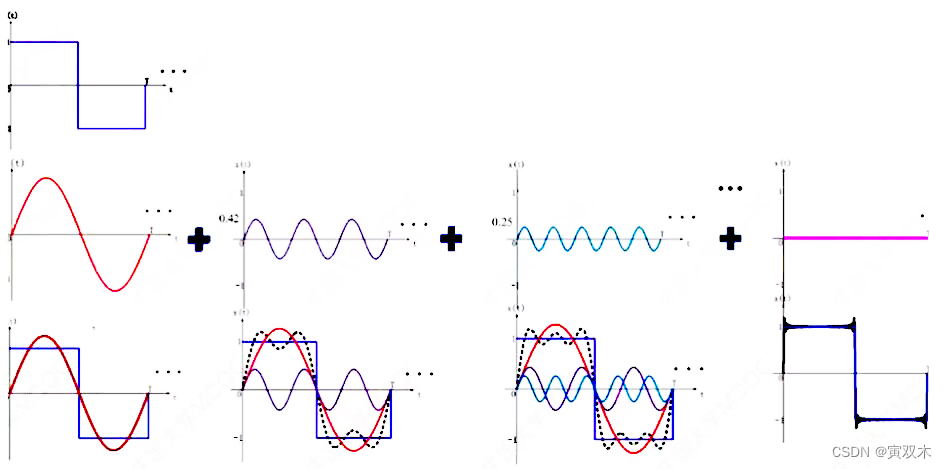
定义

连续时间信号

对于一个连续的时间域信号 𝑓(𝑡)，其傅里叶变换 𝐹(𝜔) 定义为：

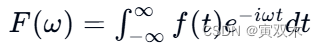
其中，𝑖 是虚数单位，𝜔 是角频率。

傅里叶逆变换是用来从频域表示恢复到时间域信号的过程，定义为：

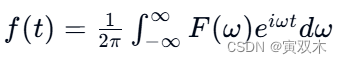
离散时间信号（了解）

傅里叶变换是一种数学技术，用于将一个函数（如时间信号）表示为不同频率的正弦波和余弦波的组合。
对于时间信号 𝑓(𝑡)，其离散傅里叶变换（DFT）可以表示为：

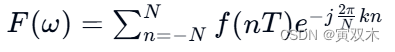
其中，N 是采样点的数量，
𝑇 是采样周期，
𝜔 是角频率，
𝑘 是从 0 到 𝑁−1 的整数，
𝑗 是虚数单位，
𝑓(𝑛𝑇) 是时间信号在时间点 𝑛𝑇 的值

逆傅里叶变换则是从频域回到时域的过程。对于离散情况，逆DFT为：

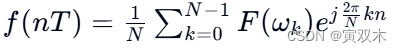
逆傅里叶变换的物理意义就是将信号从频域变回时域。
在数字信号处理中，快速傅里叶变换（FFT）算法被广泛用来计算DFT，因为它极大地减少了所需的计算量。
傅里叶变换的应用非常广泛，包括信号处理、图像处理、热传导分析、量子力学等多个领域。

---

傅里叶级数

傅里叶级数是一种将周期函数表示为其不同频率成分的数学工具
它通过将函数展开成无限个正弦和余弦函数的和来实现这一点。
如果一个函数 𝑓(𝑥)在区间2𝜋上是周期性的，即

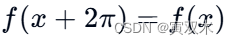
那么它可以表示为：

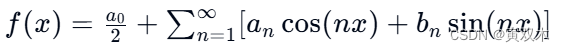
其中，𝑎0，𝑎𝑛, 和 𝑏𝑛是傅里叶系数，可以通过以下公式计算：

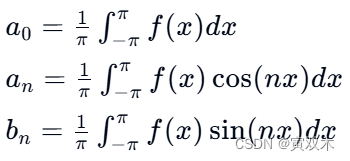
这些系数决定了函数在每个频率成分上的权重。通过计算这些系数，我们可以了解函数在不同频率上的分布情况。

---

傅里叶变换基本性质 & 简表：傅里叶变换 & 拉普拉斯变换 简表及其常见定理性质

---

傅氏变换缺陷

傅氏变换是建立在傅氏积分基础上的，一个函数除要满足狄氏条件外，还要在(-∞,+∞)上绝对可积，才有古典意义下的傅氏变换
而绝对可积是一个相当强的条件，即使是一些很简单的函数(如线性函数，正弦与余弦函数等)，都不满足此条件

引人δ函数后，傅氏变换的适用范围被拓宽了许多，使得“缓增”函数也能进行傅氏变换，但对于以指数级增长的函数仍无能为力。
另外，傅氏变换必须在整个实轴上有定义。
但在工程实际问题中，许多以时间 t 作为自变量的函数，在 t<0 时是无意义的，或者是不需要考虑的。
因此在使用傅氏变换处理问题时，具有一定的局限性.

---

二、拉普拉斯变换

为了解决傅里叶变换这些问题，拉普拉斯变换应运而生，既具有类似于傅氏变换的性质，又能克服以上的不足。

拉普拉斯变换定义

设函数 𝑓(𝑡) 在 t ≥ 0 时有定义，且积分

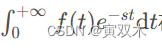
在复平面 𝑠 的某一区域内收敛，则有拉普拉斯变换：

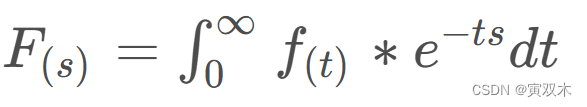
拉普拉斯逆变换

---

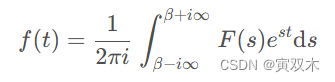
拉普拉斯变换存在条件

（第(2) 点了解）
拉普拉斯变换的存在定理 若函数𝑓(𝑡)满足下列条件：
(1) 在 𝑡 ≥ 0 的任一有限区间上连续或分段连续；
(2) 当 𝑡→ +∞ 时，**𝑓(𝑡)**的增长速度不超过某一指数函数，即存在 M > 0 和 c ≥ 0 使得

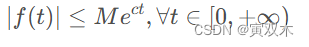
则 𝑓(𝑡) 的拉普拉斯变换 𝐹(𝑠) 在半平面 Re(s)>c 上一定存在，右端的积分在 Re( s ) ≥ c1 > c 上绝对收敛而且一致收敛，并且在 Re⁡(s) > c 的半平面内， 𝐹(𝑠) 为解析函数。 c 称为 𝑓(𝑡) 的增长指数。

---

拉普拉斯基本定理 & 简表：傅里叶变换 & 拉普拉斯变换 简表及其常见定理性质

---

三、卷积 & 卷积定理

卷积定义

卷积是信号处理中的一种基本操作，用于计算两个信号之间的相互影响或混合效果。
在数学上，它是通过一种特定的积分或求和方式来定义的，具体取决于信号是离散的，还是连续的。

离散时间信号（了解）

对于两个离散时间信号 𝑓[𝑛] 和 𝑔[𝑛] , 它们的卷积 ℎ[𝑛] 定义为:

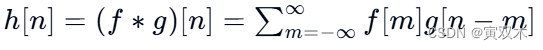
这里的求和是对所有可能的 𝑚值进行的，其中𝑛是卷积结果的索引。
离散卷积广泛应用于数字信号处理、图像处理等领域，用于模拟和分析离散时间系统的行为。

连续时间信号（重点）

对于连续时间信号 𝑓(𝑡) 和 𝑔(𝑡) ，它们的卷积 ℎ(𝑡) 定义为

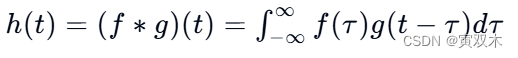
这里， 𝜏 是积分中的变量，表示时间上的推迟。
卷积运算在信号处理中非常重要，因为它描述了系统对输入信号的响应如何随着时间演变。
例如，在滤波器设计中，卷积用于计算输出信号如何由输入信号和系统响应决定。

卷积定理

卷积定理是傅里叶分析中的一个重要结果，它表明在时域中的卷积等价于频域中的乘积。具体来说，如果 𝑓(𝑡) 和 𝑔(𝑡) 是两个连续时间信号，它们的傅里叶变换分别为 𝐹(𝜔) 和 **𝐺(𝜔)** ，
那么这两个信号卷积的结果 ℎ(𝑡)=(𝑓∗𝑔)(𝑡) 的傅里叶变换 𝐻(𝜔) 满足 𝐻(𝜔) = 𝐹(𝜔)𝐺(𝜔)

同样地，在离散时间信号处理中，对于信号 𝑓[𝑛] 和 𝑔[𝑛] 的卷积 ℎ[𝑛] ，
它们的离散时间傅里叶变换（DTFT）也满足 𝐻(𝑛) = 𝐹(𝑛)𝐺(𝑛) 。
卷积定理是信号处理和通信理论中的基础，它提供了解决时域和频域问题之间转换的关键联系。

---

傅里叶变换 & 拉普拉斯变换 简表及其常见定理性质 详见：
傅里叶变换 & 拉普拉斯变换 简表及其常见定理性质

---

┈┈┈┈▕▔╲┈┈┈┈┈┈┈ ┈┈┈┈▕▔╲┈┈┈┈┈┈┈ ┈┈┈┈▕▔╲┈┈┈┈┈┈┈┈
┈┈┈┈┈▏▕┈┈┈┈┈┈┈ ┈┈┈┈┈▏▕┈┈┈┈┈┈┈ ┈┈┈┈┈▏▕┈┈┈┈┈┈┈ ┈
┈┈┈┈┈▏ ▕▂▂▂▂▂┈┈┈┈┈┈┈▏ ▕▂▂▂▂▂┈┈┈┈┈┈┈▏ ▕▂▂▂▂▂┈┈┈
▂▂▂▂╱┈┈▕▂▂▂▂▏┈ ▂▂▂▂╱┈┈▕▂▂▂▂▏┈ ▂▂▂▂╱┈┈▕▂▂▂▂▏┈┈
▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈ ▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈ ▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈
▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈ ▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈ ▉▉▉┈┈┈┈▕▂▂▂▂▏ ┈
▔▔▔▔╲▂▂▕▂▂▂▂▏┈ ▔▔▔▔╲▂▂▕▂▂▂▂▏┈ ▔▔▔▔╲▂▂▕▂▂▂▂▏┈┈

如果对你有帮助，就点赞收藏把！(｡･ω･｡)ﾉ♡