先抛一个问题，一副扑克牌随机发牌，均匀发给三人，已知你手上有两张K，另外两张K，每人一张的概率大，还是分给一个人的概率大，或者这两种场景概率一样？

        从小开始学数学，但毕业后全都还给了老师，只是为了学（考试）而学。

       16年开始，拜读了吴军老师的《数学之美》一书，初步感受到了数学的魅力，然后开始有意或无意的学习一些数学知识，并尝试于工作中运用一些数学思维。最近又拜读了吴军老师的《吴军数学通识讲义》一书，逐渐被她所吸引。现在记录一些自己的想法，分享一些数学给我带来的帮助。

        一、抽象能力的提升。会尝试抽取共性，由个例上升到规律。

        早两天，我女儿给我介绍她做的华容道游戏规则说明书，上面写了一个具体的案例，然后说明基于该案例如何移动，以完成游戏。我问她，如果换一个案例，按照游戏规则说明书，能否完成游戏。她意识到了问题，然后重新设计了游戏规则说明书。她的问题在于用个例来说明规则，但个例不具有普适性。

        勾三股四弦五，勾股定理，是我们初中学的经典数学定理之一，在国外，被称为毕达哥拉斯定理。但在古埃及人建造大金字塔时就已经按照勾股数在设计墓室的尺寸了，比毕达哥拉斯生活的年代早了约2000年，为什么会称为毕达哥拉斯定理？勾三股四弦五，包括古埃及使用的勾股数，都只是个例，没有描述共性，即规律。他们的共性是：直角边的平方和等于斜边的平方。

        基于这个视角来审视我的工作，自能辨识出产品设计的优劣。

        二、理性的看待问题。用数据说法，而非感觉。

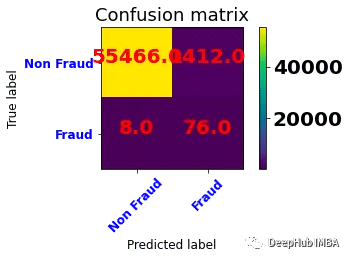
        以本文开始的扑克牌案例说明，我的第一感觉是两种场景的概率一样大，而实际是每人一张的概率更大。第一个人拿到第一张K的概率为：1/36 * 18，共36张牌，K分布的概率是均等的，即1/36，第一个人有18张牌，于是有1/2的几率拿到第一张牌。拿到第一张后拿到第二张K的概率为: 1/35 * 17，由于一张牌被K占用，只有35张牌（空位），第一个人手上只有17张牌（空位）。两个人，均有可能拿到两张K，最终两张牌被一个拿到的概率略小于1/2，而平分的概率略大于1/2。

        三、简单是美。同样的效果，用简单的方案。好的方案，在逻辑上，应该是简单的。

        四、动态、变化的眼光看问题。

        ... ...

        想表达的有很多，但受限于个人能力，如同茶壶里煮饺子——有嘴倒(道)不出。

        重新拾起这些数学知识后，感觉打开了一扇新的窗户，回顾以前学习的知识，时常有耳目一新的感觉。我想，她可能在升级我的认知。

        树，包括根系和树冠。二者各有其价值所在，根系的大小和树冠的大小是成正比的，根系是大树的地基。作为工作十多年的老兵，深深感受到元能力（学习、理解、抽象、思辨等）的重要性，他就是我们的地基。而数学、逻辑学、语文、自然科学、哲学等通识教育，会帮助我们夯实地基。