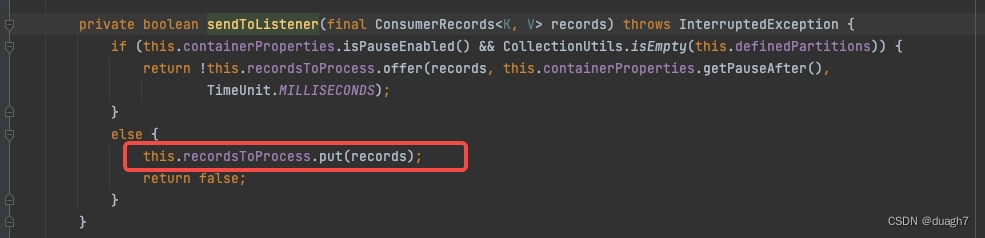
一、 问题描述

 二、算法思想  

       首先，我们需要判断一个数列是否是接龙数列。可以通过遍历数列的每一个元素，判断该元素的首位数字是否等于前一个元素的末位数字。如果所有元素都满足条件，则该数列是接龙数列。

       接下来，我们需要计算最少删除多少个数才能将数列变成接龙数列。可以使用动态规划的方法解决这个问题。令dp[i]表示长度为i的数列中最少删除的数的个数。对于dp[i]，我们可以分为两种情况来考虑：

1. 删除第i个数，即dp[i] = dp[i-1] + 1；
2. 保留第i个数，即dp[i] = dp[i-1]。

       然后，我们需要判断第i个数是否可以和第i-1个数连接起来形成一个接龙数列。如果可以，则dp[i]取上述两种情况中较小的一个；如果不可以，则只能删除第i个数。

最后，我们取dp数组中的最大值作为最终答案，即为最少删除的数的个数。

具体实现时，我们可以使用一个辅助数组numCount来记录每个首位数字的出现次数。遍历数列的每一个元素，判断该元素的首位数字是否等于前一个元素的末位数字，然后更新numCount数组和dp数组。最后返回dp数组中的最大值即可。

三、代码实现 

#include<stdio.h>
int main()
{
    int a=0,b=0;
    int n=0,amount=0;
    int dp[10]={0},number=0;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
            scanf("%d",&number);
            b=number%10;
            while(number>=10)
            {
                a=number/10;
                number/=10;
            }
            dp[b]=dp[a]+1>dp[b]?dp[a]+1:dp[b];
            if(dp[b]>amount)
            {
                amount=dp[b];
            }
    }
        printf("%d",n-amount);
}

执行结果   

 结语  

志在山顶的人

不会贪念山腰的风景

！！！