目录
step函数(求阶跃响应):
impulse函数(求脉冲响应):
lsim函数(求输出):
1,求二阶系统不同阻尼比条件下的阶跃响应曲线
2,求二阶负反馈系统的动态性能指标
利用MATLAB可以方便地进行控制系统的时域分析。洋相判断系统的稳定性,只要求出系统的闭环极点,即闭环传递函数的分母多项式的根即可,而分析系统的动态特性,只要求出系统的阶跃响应即可。
利用MATLAB控制系统工具箱中所提供的求联系系统的单位阶跃响应函数step(),单位冲激响应函数impluse(),任意输入信号下的响应函数lsim()等函数可以方便的求出系统在该信号作用下的响应。
step函数(求阶跃响应):
step(num,den)
num表示分子各阶系数,den表示分母各阶系数
作用:已知闭环传递函数,求其阶跃响应
step(num,den)会输出图像;ct2=step(num,den)输出数值。
impulse函数(求脉冲响应):
impulse(num,den)
num表示分子各阶系数,den表示分母各阶系数
作用:已知闭环传递函数,求其脉冲响应
impulse(num,den)会输出图像;ct2=impulse(num,den)输出数值。
lsim函数(求输出):
lsim(sys,u,t)
sys传递函数,u 输入函数,t时域自变量
作用:已知输入函数和传递函数,用这个可以的到每次系统的输入对应的输出(输入函数u要是时域中的,可以输出图像也可以是对应的值)
1,求二阶系统不同阻尼比条件下的阶跃响应曲线
已知典型二阶系统的传递函数为
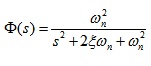
假设Wn=1,试在同一张图上绘制当阻尼比分别为0、0.1、0.3、0.5、0.7、1、2时系统的单位阶跃曲线
dum=[4];
den1=[1 0 4];
den2=[1 0.4 4];
den3=[1 1.2 4];
en4=[1 2 4];
den5=[1 2.8 4];
den6=[1 4 4];
den7=[1 8 4];
sys1=tf(dum, den1);
sys2=tf(dum, den2);
sys3=tf(dum, den3);
sys4=tf(dum, den4);
sys5=tf(dum, den5);
sys6=tf(dum, den6);
sys7=tf(dum, den7);
step(sys1, sys2, sys3, sys4, sys5, sys6, sys7);
可以看到阻尼比为0时无法收敛,其他阻尼比均收敛
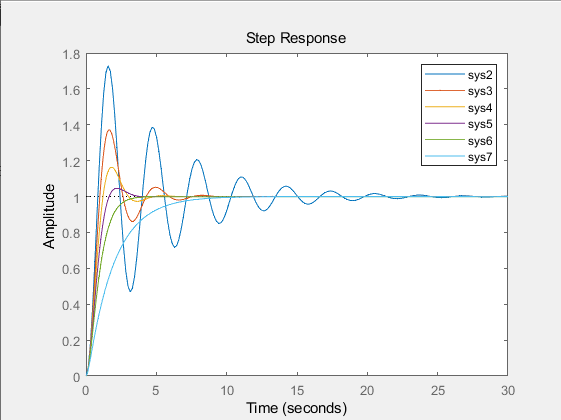
2,求二阶负反馈系统的动态性能指标
设单位负反馈二阶系统的开环传递函数为
G(s)=1.25/s²+s
试计算系统的动态性能指标:上升时间tr、峰值时间tp、超调量、调整时间ts
clear
num=1.25;
den=[1 1 0];
sys=tf(num,den);%建立系统开环传递函数模型
sys=feedback(sys,1);%建立系统闭环传递函数模型
[y,t]=step(sys);%求系统单位阶跃响应
ytr=find(y>=1);
rise_time=t(ytr(1))%计算上升时间
[ymax,tp]=max(y);
peak_time=t(tp)%计算峰值时间
max_overshoot=ymax-1%计算超调量
s=length(t);
while y(s)>0.98&y(s)<1.02
s=s-1;
end
settling_time=t(s+1)%计算调整时间
plot(t,y,'k',t,ones(length(t),1),'k-.')%绘制响应曲线
axis([0 10 0 2.2])
title('Plot of Unit-Setp Response Curves','Position',[5 2.22],'FontSize',8)
xlabel('Time(sec)')
ylabel('Response')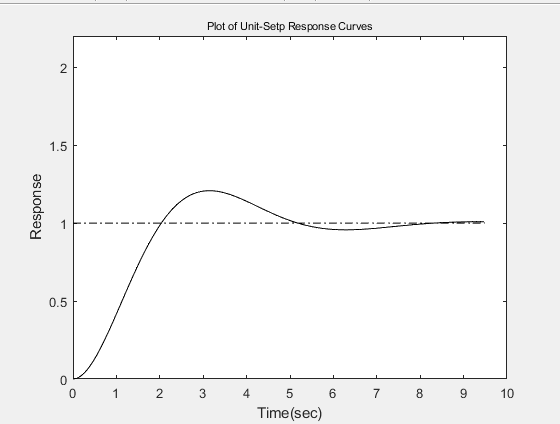






![[GXYCTF2019]luck_guy1题解](https://img-blog.csdnimg.cn/img_convert/9802c8db9a7ada5cbeea23f2a6b413cb.jpeg)