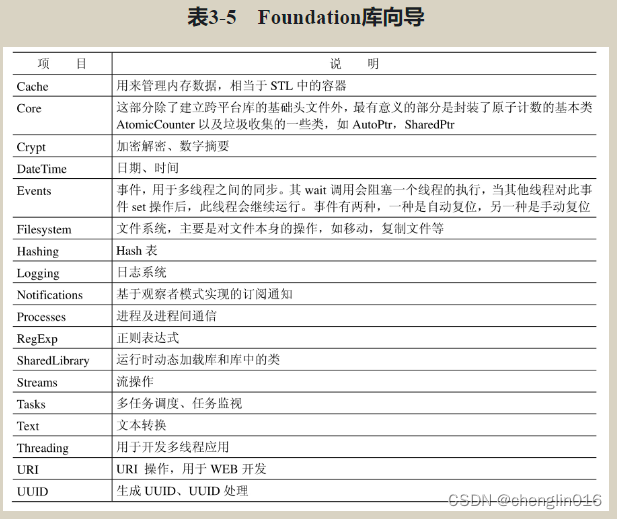
🎯要点

🎯达朗贝尔一维波动通解，二维变速模拟 | 🎯达朗贝尔算子解双曲波形微分方程 | 🎯耗散系统粘性伯格斯方程快速傅里叶变换算法 | 🎯二维线性和非线性对流扩散解和湍流隐式建模

📜偏微分方程用例：Python自动造波器椭圆曲线波孤子解

📜有限差分用例：Python微磁学磁倾斜和西塔规则算法

🍇Python一维粘性伯格斯方程

一维空间中粘性伯格斯方程的一般形式是耗散系统：
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=\nu \frac{{\partial }^{2}u}{\partial x^2}$$
此项 $u\partial u/\partial x$ 也可以重写为 $\partial \left(u^2/2\right)/\partial x$。当扩散项不存在时（即 $\nu =0$​ ），粘性伯格斯程变为无粘伯格斯方程：
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=0$$
这是可以产生不连续性（冲击波）的守恒方程的原型。

当人们检查等式的左侧时，$\nu$ 的小值形成锐梯度的原因就变得直观清楚了。此项 $\partial /\partial t+u\partial /\partial x$ 显然是一个波算子，描述以 $u$ 速度沿正 $x$ 方向传播的波。由于波速为$u$，表现出较大$u$值的区域将比表现出较小$u$值的区域更快地向右传播；换句话说，如果 $u$ 最初沿 $x$ 方向减小，则位于背面的较大 $u$ 将赶上位于正面的较小 $u$ 。右侧扩散项的作用本质上是阻止梯度变得无穷大。

在此，我们将使用非线性对流和扩散，仅创建一维伯格方程。
$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=\nu \frac{{\partial }^{2}u}{\partial x^2}$$
我们可以离散化这个微分，采用以下形式：
$$\frac{u_i^{n+1}-u_i^n}{\Delta t}+u_i^n\frac{u_i^n-u_{i-1}^n}{\Delta x}=v\frac{u_{i+1}^n-2u_i^n+u_{i-1}^n}{\Delta x^2}$$
在解决了未知数之后，我们得到了用 Python 编码的算法。
$$u_i^{n+1}=u_i^n-u_i^n\frac{\Delta t}{\Delta x}\left(u_i^n-u_{i-1}^n\right)+v\frac{\Delta t}{\Delta x^2}\left(u_{i+1}^n-2u_i^n+u_{i-1}^n\right)$$
速度的初始条件是使用以下函数创建的：
$$\begin{array}{rl}u& =-\frac{2v}{\varphi }\frac{\partial \varphi }{\partial x}+4\\ \varphi & =\exp \left(\frac{-x^2}{4v}\right)+\exp \left(\frac{-(x-2\pi {)}^2}{4v}\right)\end{array}$$
边界条件意味着周期性，由下式给出：
$$u(0)=u(2\pi )$$
有一个解析解：
$$\begin{array}{rl}& u=-\frac{2v}{\varphi }\frac{\partial \varphi }{\partial x}+4\\ & \varphi =\exp \left(\frac{-(x-4t{)}^2}{4v(t+1)}\right)+\exp \left(\frac{-(x-4t-2\pi {)}^2}{4v(t+1)}\right)\end{array}$$
解该问题的Python代码如下：

import numpy as np
import sympy as sp
import pylab as pl
pl.ion()

x, nu, t = sp.symbols('x nu t')
phi = sp.exp(-(x-4*t)**2/(4*nu*(t+1))) + sp.exp(-(x-4*t-2*np.pi)**2/(4*nu*(t+1)))

phiprime = phi.diff(x)
u = -2*nu*(phiprime/phi)+4

from sympy.utilities.lambdify import lambdify
ufunc = lambdify ((t, x, nu), u)

nx = 101 
nt = 100 
dx = 2*np.pi/(nx-1) 
nu = 0.07 
dt = dx*nu 
T = nt*dt 

grid = np.linspace(0, 2*np.pi, nx) 
un = np.empty(nx) 
t = 0
u = np.asarray([ufunc(t, x, nu) for x in grid])

pl.figure(figsize=(11,7), dpi=100)
pl.plot(grid,u, marker='o', lw=2)
pl.xlim([0,2*np.pi])
pl.ylim([0,10])
pl.xlabel('X')
pl.ylabel('Velocity') 
pl.title('1D Burgers Equation - Initial condition')

for n in range(nt): 
    un = u.copy()
    for i in range(nx-1):
        u[i] = un[i] - un[i] * dt/dx * (un[i]-un[i-1]) + \
            nu * dt/(dx**2) * (un[i+1] - 2*un[i] + un[i-1])

    u[-1] = un[-1] - un[-1] * dt/dx * (un[-1]-un[-2]) + \
            nu * dt/(dx**2) * (un[0] - 2*un[-1] + un[-2])

u_analytical = np.asarray([ufunc(T, xi, nu) for xi in grid])

pl.figure(figsize=(11,7), dpi=100)
pl.plot(grid, u, marker='o', lw=2, label='Computational')
pl.plot(grid, u_analytical, label='Analytical')
pl.xlim([0, 2*np.pi])
pl.ylim([0,10])
pl.legend()
pl.xlabel('X')
pl.ylabel('Velocity') 
pl.title('1D Burgers Equation - Solutions')

👉参阅：计算思维 | 亚图跨际