文章目录
- 前言
- 一、SVPWM的控制原理
- 二、空间矢量的概念
- 三、电压与磁链空间矢量的关系
- 四、三相逆变器的基本电压空间矢量
- 五、SVPWM 算法的合成原理
- 六、SVPWM 算法推导
- 6.1.七段式SVPWM
- 6.2.五段式SVPWM(又称DPWM)
- 七、SVPWM 算法实现
- 7.1.合成矢量Uref所处扇区的判断
- 7.2.基本电压空间矢量作用时间计算
- 7.3.扇区矢量切换点的确定
- 7.4.PWM信号生成
- 八、七段式SVPWM仿真分析
- 8.1.仿真电路分析
- 8.2.仿真结果分析
- 九、五段式SVPWM仿真分析
- 9.1.仿真结果分析
- 十、PMSM电压开环控制Matlab/Simulink仿真分析
- 10.1.仿真电路分析
- 10.2.仿真结果分析
- 总结
前言
本章节首先介绍SVPWM控制技术的原理,然后详细分析SVPWM控制算法的具体实现方式,并通过Matlab/Simulink对SVPWM控制算法进行仿真分析,最后通过永磁同步电机矢量控制的实例进行算法实现。
一、SVPWM的控制原理
SPWM控制技术主要控制逆变器的输出电压尽量接近正弦波,并未顾及输出电流的波形。电流滞环跟踪控制则直接控制输出电流接近正弦波。
有关PWM控制技术请阅读:
PWM控制技术+Simulink仿真详解
交流电机需要输入三相正弦电流的最终目的是在电机空间形成圆形旋转磁场,从而产生恒定的电磁转矩。把逆变器和交流电机视为一体,以圆形旋转磁场为目标来控制逆变器的工作,这种控制方法称做“磁链跟踪控制”,磁链轨迹的控制是通过交替使用不同的电压空间矢量实现的,所以又称为“电压空间矢量PWM(Space Vector PWM,SVPWM)控制”。
实践和理论证明,与直接的 SPWM 技术相比,SVPWM 算法的主要优点有:
1、SVPWM优化谐波程度比较高,消除谐波效果要比SPWM好,容易实现,并且可以提高电压利用率,输出电压最高可提高15%左右。
2、SVPWM算法提高了电压源逆变器的直流电压利用率和电机的动态响应速度,同时减小了电机的转矩脉动等缺点。
3、SVPWM比较适合于数字化控制系统。
二、空间矢量的概念
在三相逆变器控制中,通常输入输出三相变量要分别描述,若能将三相变量用一个合成量表示,并保持信息的完整性,则三相的问题将简化为单向的问题,由此引入空间矢量的概念。

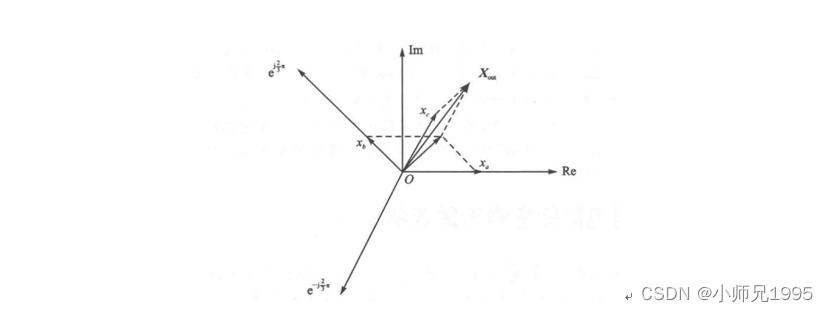



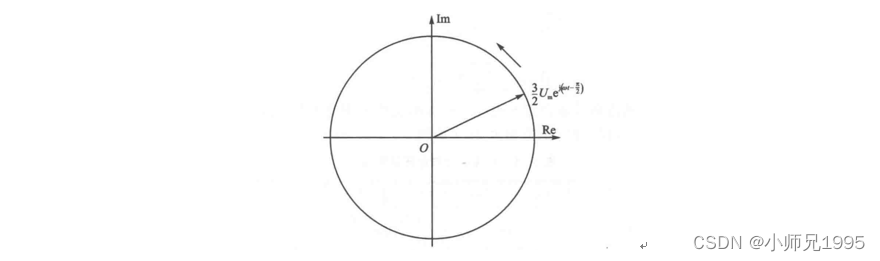
三、电压与磁链空间矢量的关系



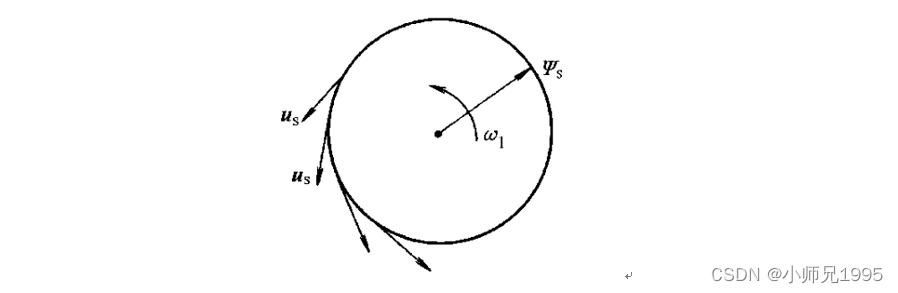
四、三相逆变器的基本电压空间矢量
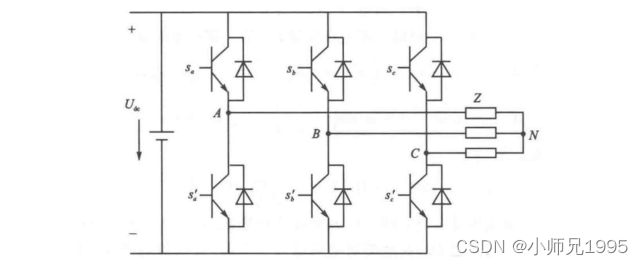

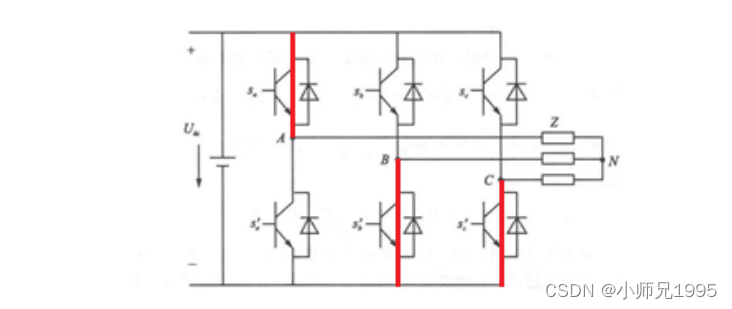
此时等效电路为:
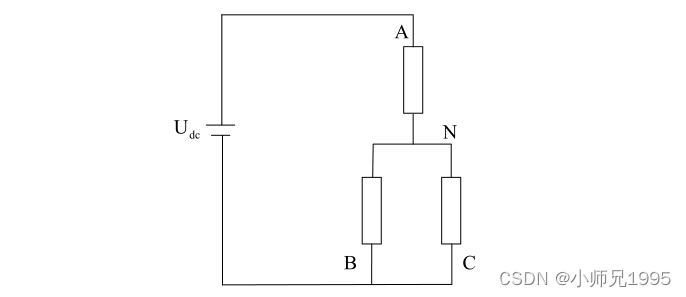
由此可推出:
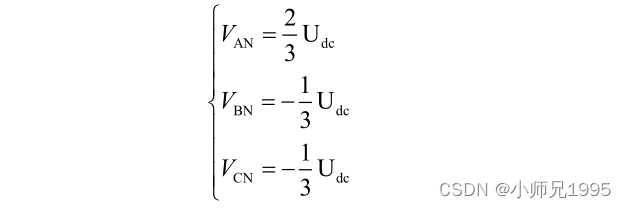
同理,可推出其他组合的电压空间矢量如下表所示:
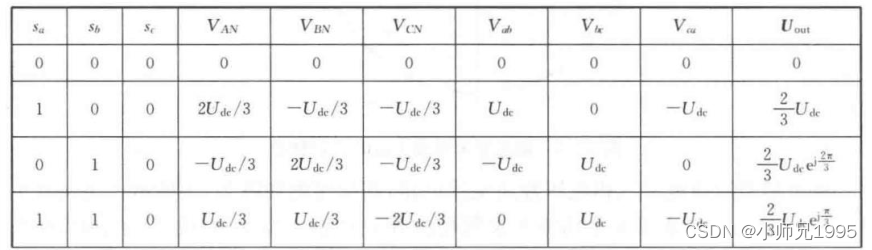
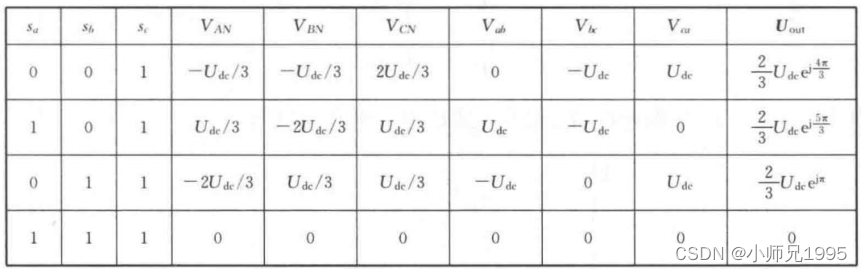

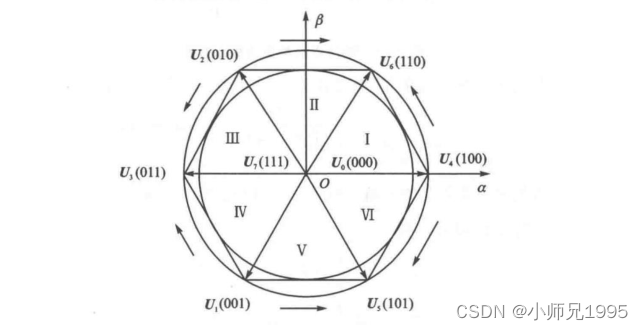
五、SVPWM 算法的合成原理


由上述分析三相正弦波电压在电压空间向量中合成一个等效的旋转电压矢量,其旋转速度为输入的电源角频率,该等效旋转电压矢量的运动轨迹为圆形。所以要产生三相正弦波电压,可以利用以上电压空间矢量合成的技术,在电压空间向量上,将设定的电压向量由一起始位置开始如 100,每次增加一个小增量,每个小增量设定的电压向量可以用该区中相邻的两个基本非零向量与零电压矢量予以合成,如此所得到的设定电压向量就等效为一个在电压空间向量平面上平滑旋转的电压空间矢量,从而达到电压空间矢量脉宽调制的目的。
六、SVPWM 算法推导





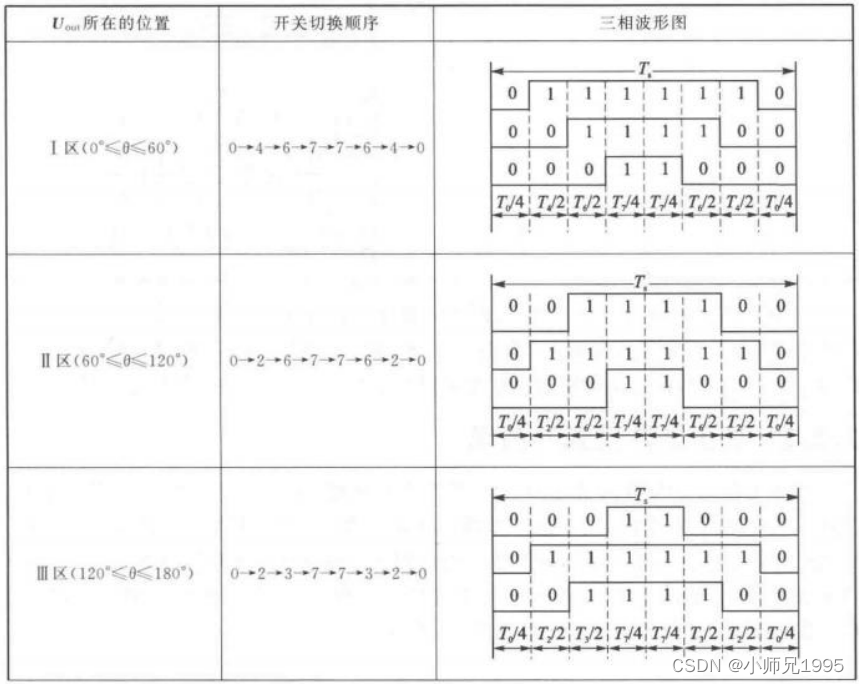
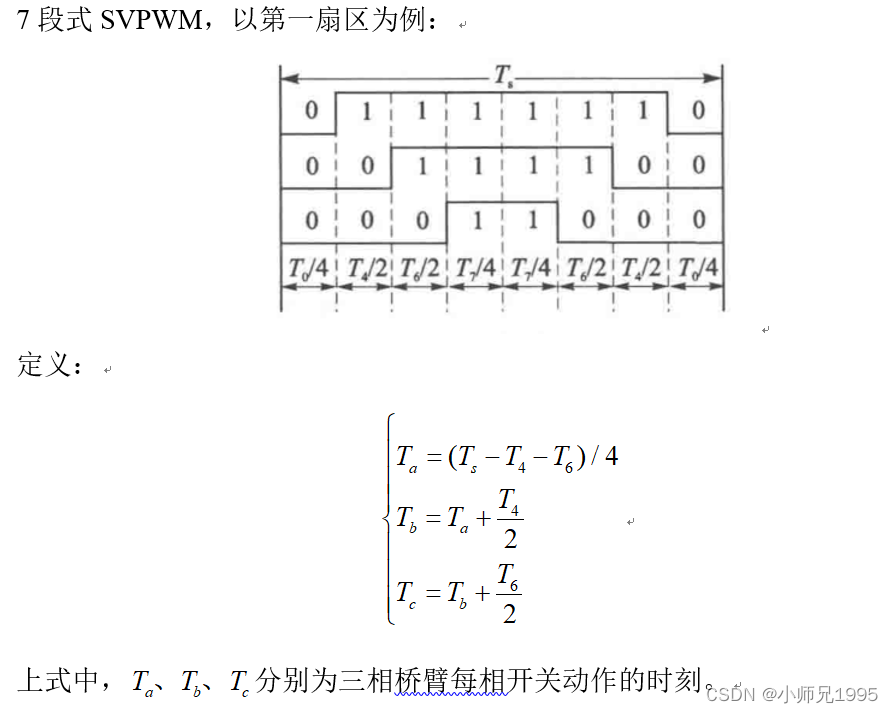
6.1.七段式SVPWM
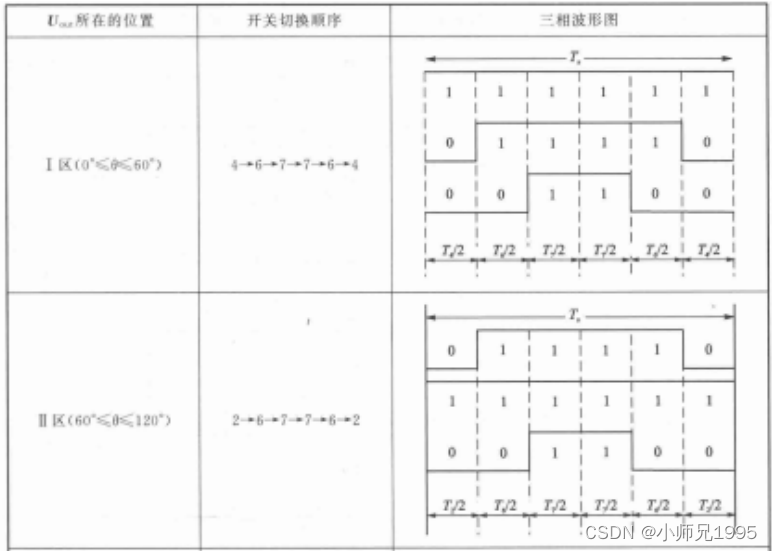
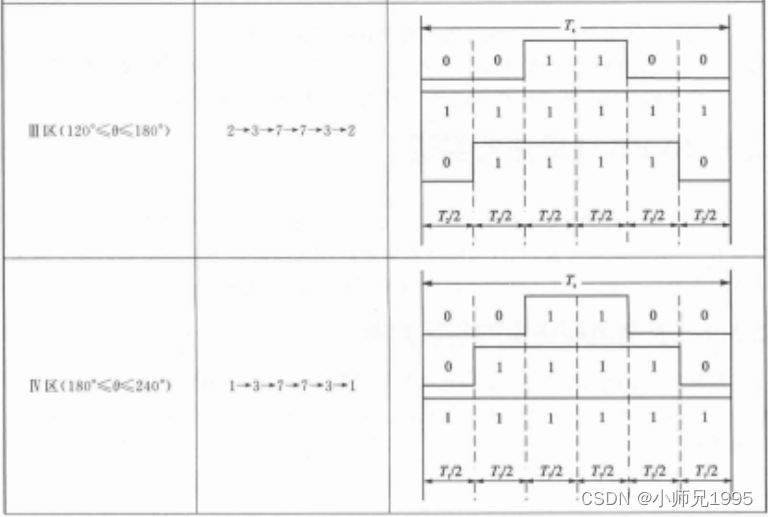
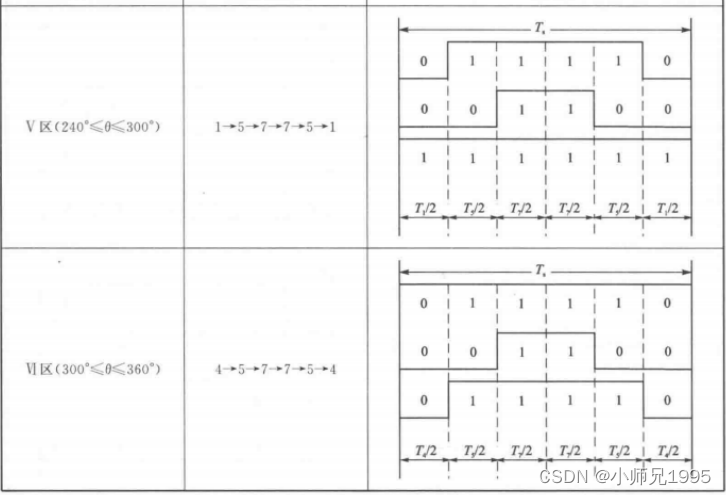
以减少开关次数为目标,将基本矢量作用顺序的原则选定为:在每次开关状态转换时,只改变其中一相的开关状态。并且对零矢量在时间上进行了平均分配,以使产生的 PWM 对称,从而有效的降低 PWM 的谐波分量。例如当从 100变为 000 时只需要改变 A 相桥臂上下开关管的状态,当从 100 变为 111 则需要改变 BC 两相桥臂上下开关管的状态,这种方式增加了一倍的开关损耗。因此,要改变电压向量 100、010、001 的大小需配合零电压矢量 000,要改变110、011、101 的大小需配合零电压矢量 111。这样通过在不同区间内安排不同的开关切换顺序,就可以获得对称的输出波形,其他各扇区的开关顺序如下所示:
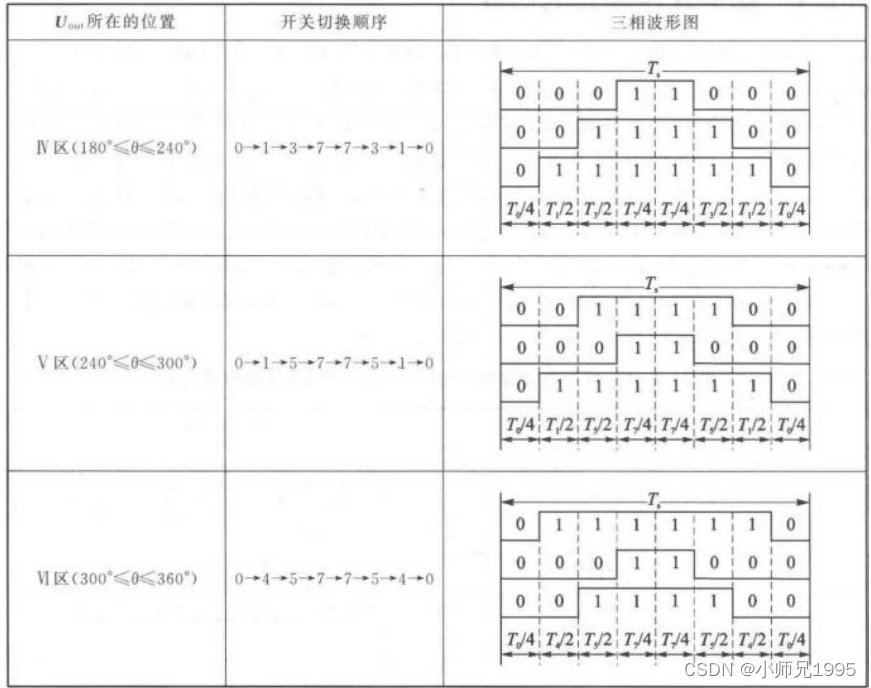

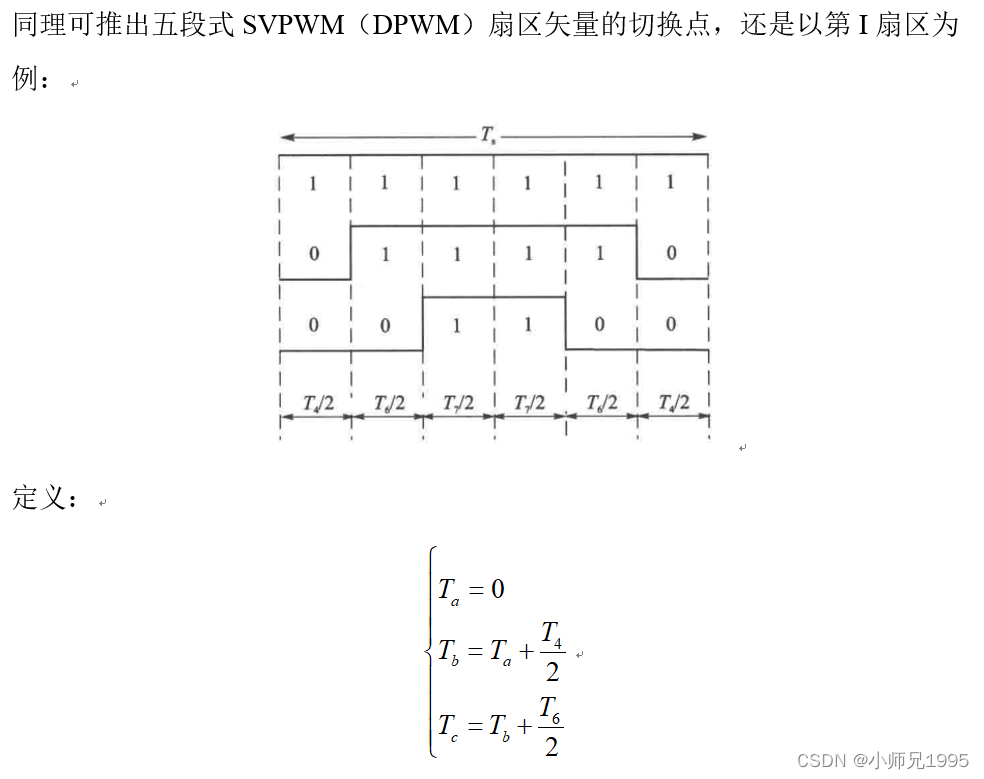
6.2.五段式SVPWM(又称DPWM)

七、SVPWM 算法实现


7.1.合成矢量Uref所处扇区的判断






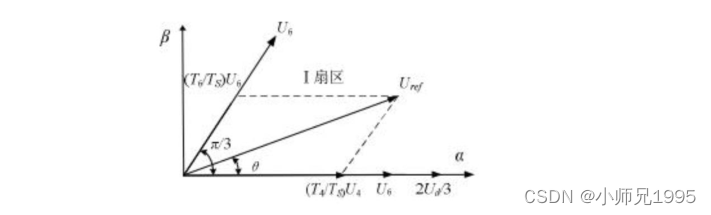
7.2.基本电压空间矢量作用时间计算
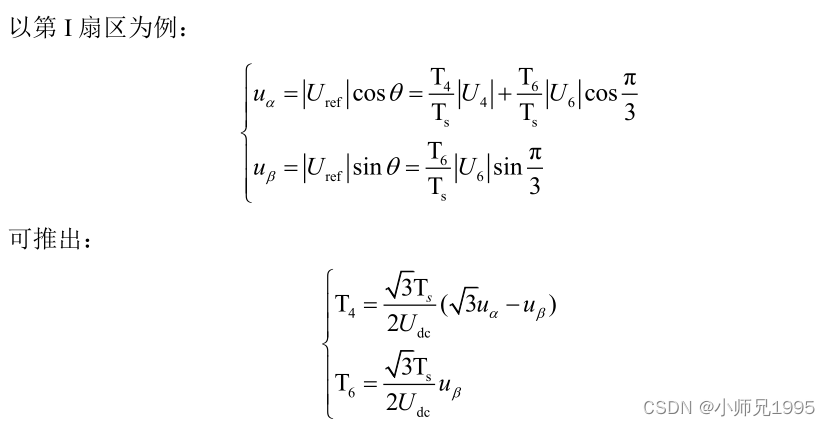

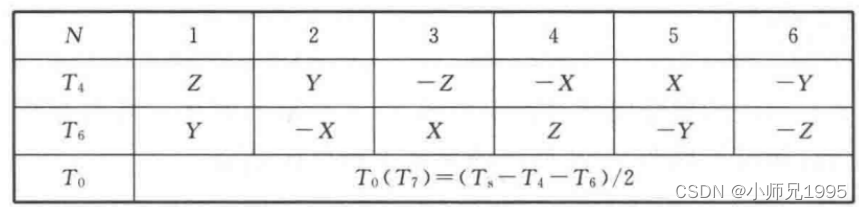
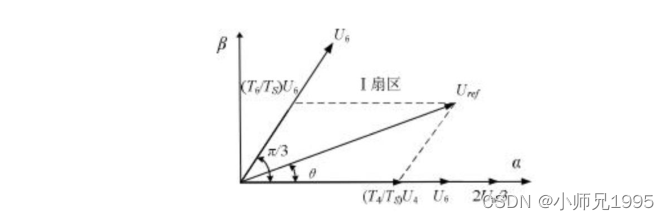
当两个零矢量作用时间为 0 时,一个 PWM 周期内非零电压矢量的作用时间最长,此时的合成空间电压矢量幅值最大。从下图可知其最大幅值不会超过图中所示的正六边形边界,而当合成矢量落在该边界之外时,将发生过调制,逆变器输出电压波形将发生失真。在 SVPWM 调制模式下,逆变器能够输出的最大不失真圆型旋转电压矢量为下图所示虚线正六边形的内切圆,其幅值为:

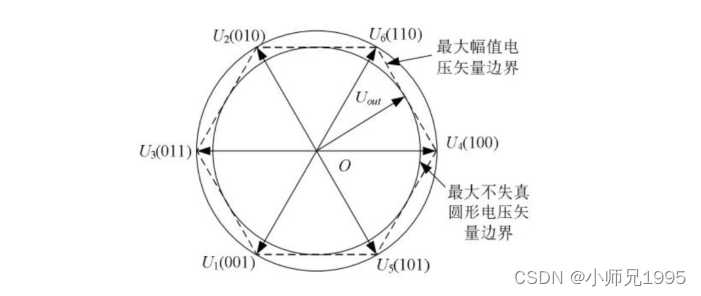


按照上述过程,就能得到每个扇区相邻两电压空间矢量和零电压矢量的作用时间。当Uref所在的扇区和对应有效电压矢量的作用时间确定后,再根据 PWM调制原理,计算出每一相对应比较器的值。
7.3.扇区矢量切换点的确定
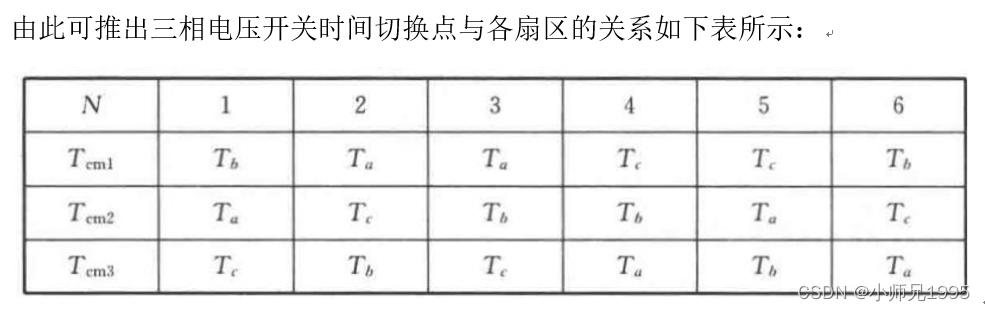
7.4.PWM信号生成
扇区矢量切换点确定后,用一定频率的三角载波信号与各个扇区矢量切换点进行比较,从而产生逆变器所需的PWM控制信号。
八、七段式SVPWM仿真分析
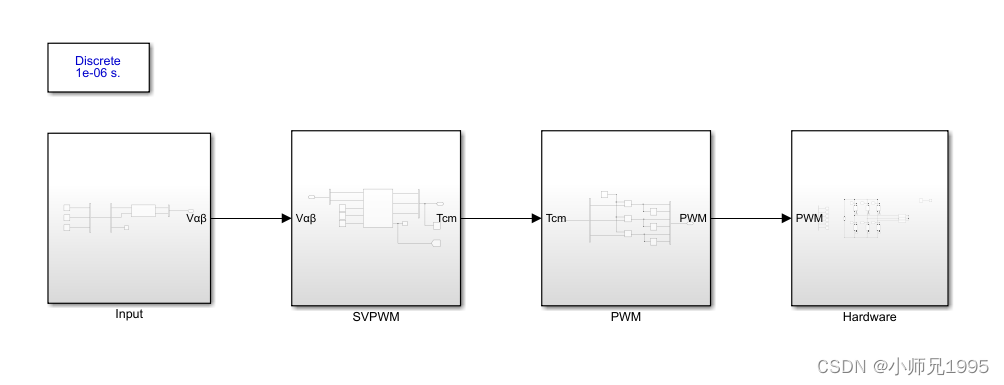
8.1.仿真电路分析
信号输入:幅值为2,频率为50Hz的三相正弦波信号
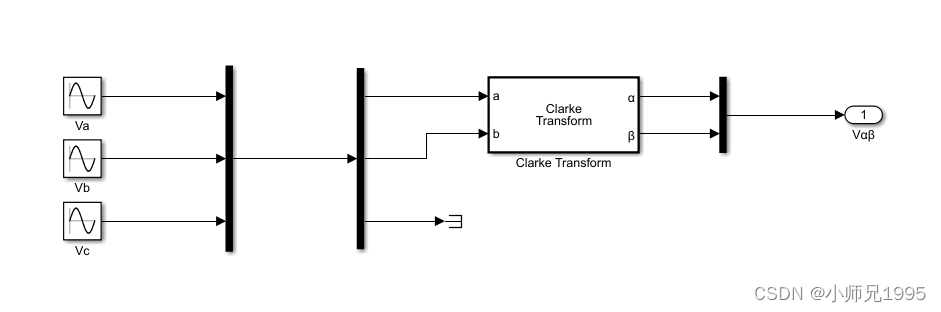
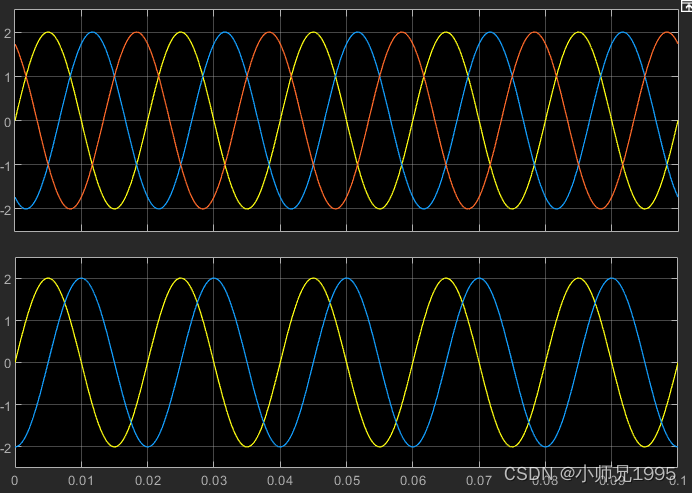
SVPWM算法实现:载波为20KHz的三角波,三相逆变电路的直流侧电压为24V
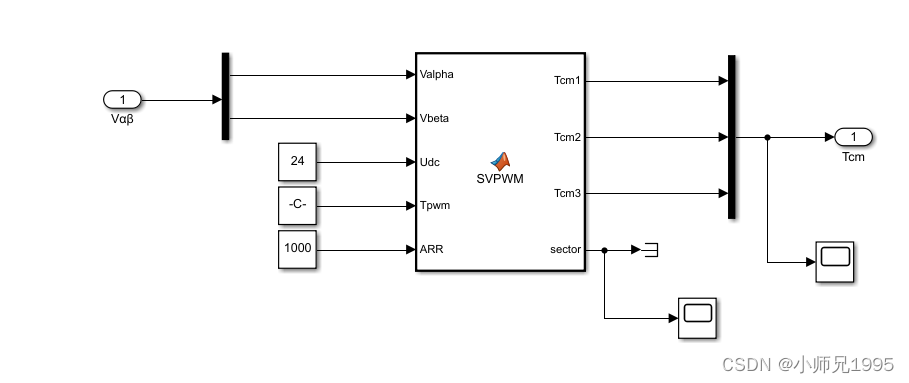
function [Tcm1,Tcm2,Tcm3,sector] = SVPWM(Valpha,Vbeta,Udc,Tpwm,ARR)
%输出变量初始化
Tcm1 = 0;
Tcm2 = 0;
Tcm3 = 0;
sector = 0;
%扇区计算
%N与扇区对应的关系
% 3 1 5 4 6 2
% I II III IV V VI
Vref1 = Vbeta;
Vref2 = (sqrt(3)*Valpha-Vbeta)/2;
Vref3 = (-sqrt(3)*Valpha-Vbeta)/2;
if(Vref1>0)
sector = 1;
end
if(Vref2>0)
sector = sector+2;
end
if(Vref3>0)
sector = sector+4;
end
%扇区内合成矢量作用时间计算
X = sqrt(3)*Vbeta*Tpwm/Udc;
Y = Tpwm/Udc*(3/2*Valpha+sqrt(3)/2*Vbeta);
Z = Tpwm/Udc*(-3/2*Valpha+sqrt(3)/2*Vbeta);
switch(sector)
case 1
T1 = Z;T2 = Y;
case 2
T1 = Y;T2 = -X;
case 3
T1 = -Z;T2 = X;
case 4
T1 = -X;T2 = Z;
case 5
T1 = X;T2 = -Y;
otherwise
T1 = -Y;T2 = -Z;
end
%过调制处理
if(T1+T2>Tpwm)
T1 = Tpwm*T1/(T1+T2);
T2 = Tpwm*T2/(T1+T2);
else
T1 = T1;
T2 = T2;
end
%扇区内合成矢量切换点时间计算
%此处为7段式,两个零矢量000 111 111插在中间,000均分插在两端
ta = (Tpwm-(T1+T2))/4;
tb = ta+T1/2;
tc = tb+T2/2;
%输出调制信号
switch(sector)
case 1
Tcm1 = tb;
Tcm2 = ta;
Tcm3 = tc;
case 2
Tcm1 = ta;
Tcm2 = tc;
Tcm3 = tb;
case 3
Tcm1 = ta;
Tcm2 = tb;
Tcm3 = tc;
case 4
Tcm1 = tc;
Tcm2 = tb;
Tcm3 = ta;
case 5
Tcm1 = tc;
Tcm2 = ta;
Tcm3 = tb;
case 6
Tcm1 = tb;
Tcm2 = tc;
Tcm3 = ta;
end
%调制信号处理,生成输入到MCU中的调制信号
Tcm1 = 2*Tcm1/Tpwm;
Tcm2 = 2*Tcm2/Tpwm;
Tcm3 = 2*Tcm3/Tpwm;
Tcm1 = Tcm1*ARR;
Tcm2 = Tcm2*ARR;
Tcm3 = Tcm3*ARR;
end
PWM信号生成:载波为20KHz的三角波
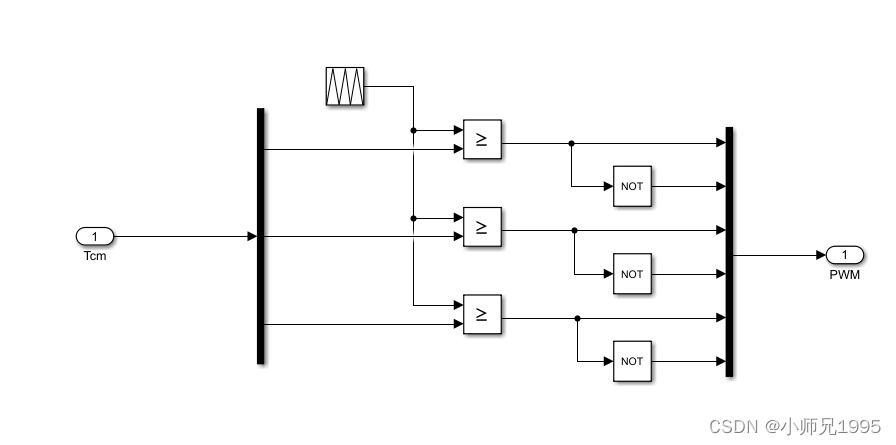
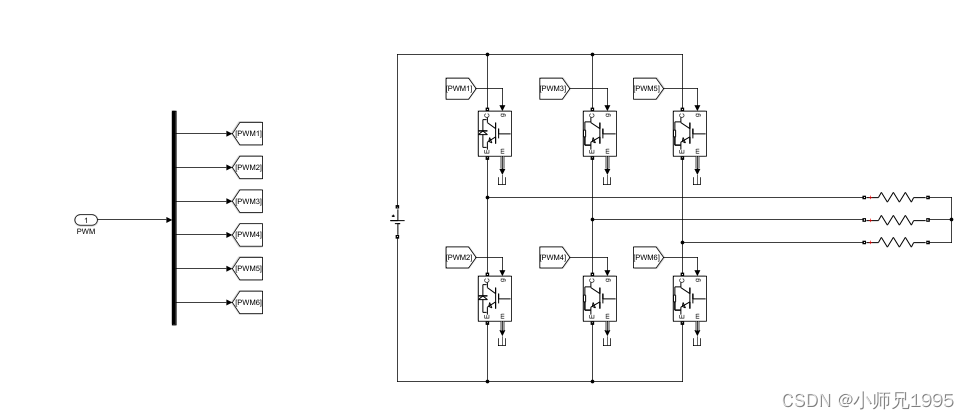
硬件电路:
8.2.仿真结果分析
电压空间矢量的运动轨迹:
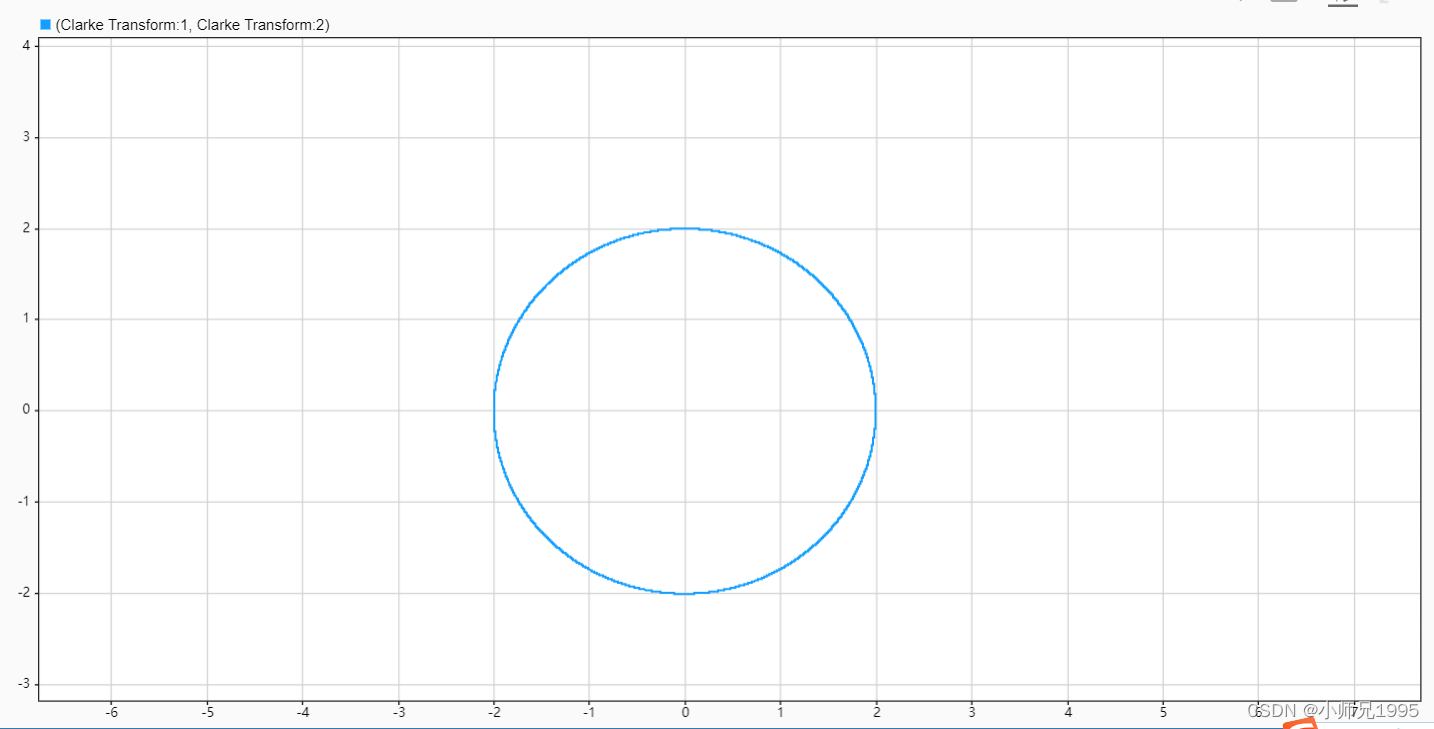
扇区判断结果:
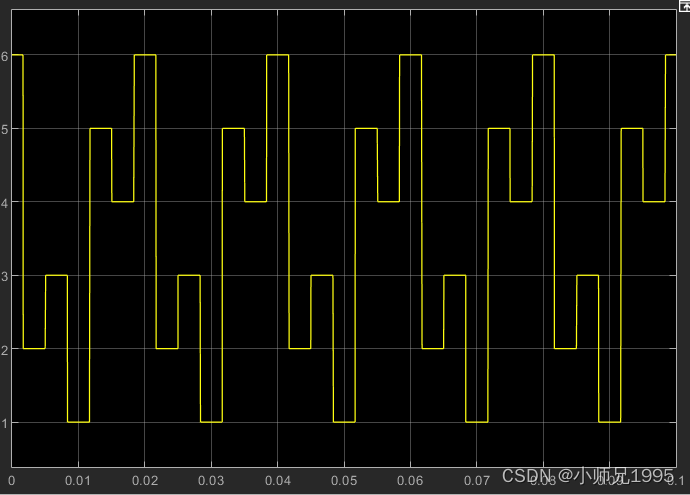
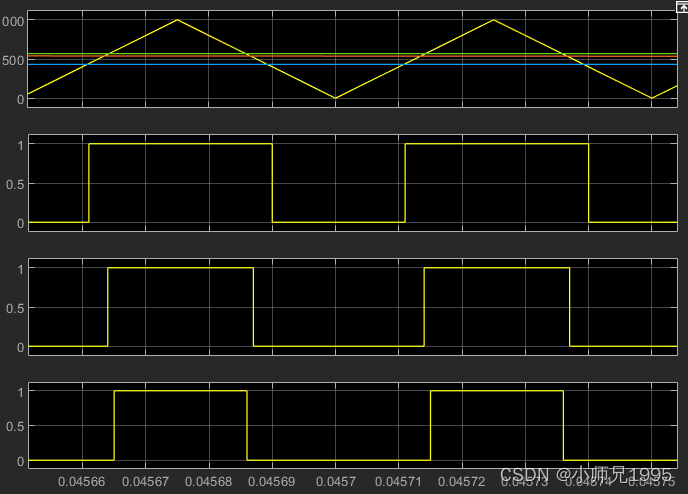
扇区内矢量切换点,即调制波波形:
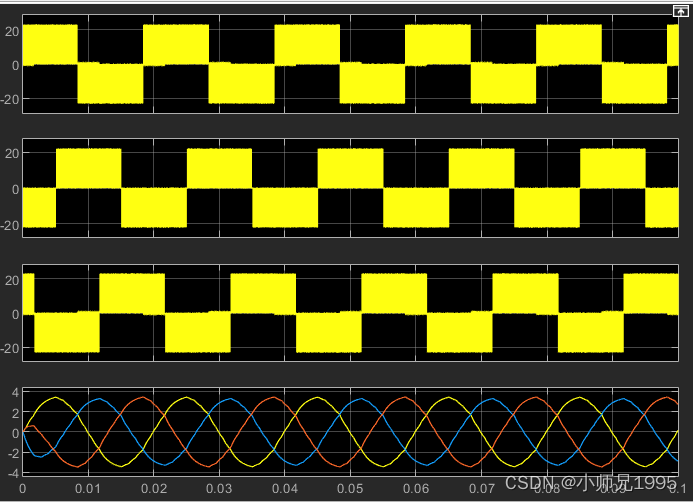
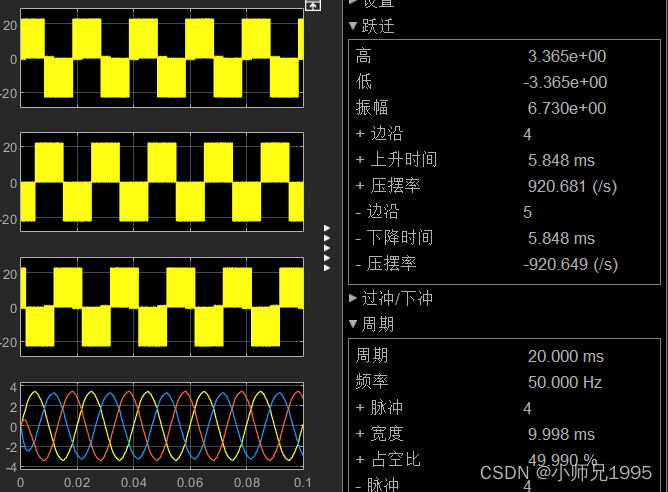
PWM信号:
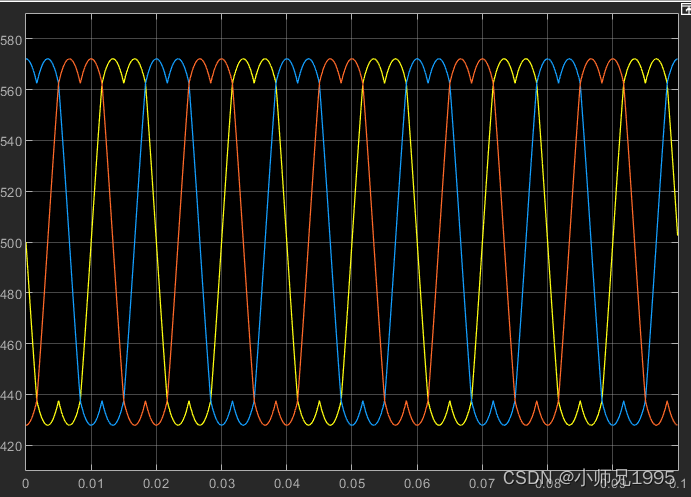
三相相电压及滤波后的三相相电压波形:生成的三相正弦电压与期望的输入电压参数一致,幅值为2,频率为50Hz。

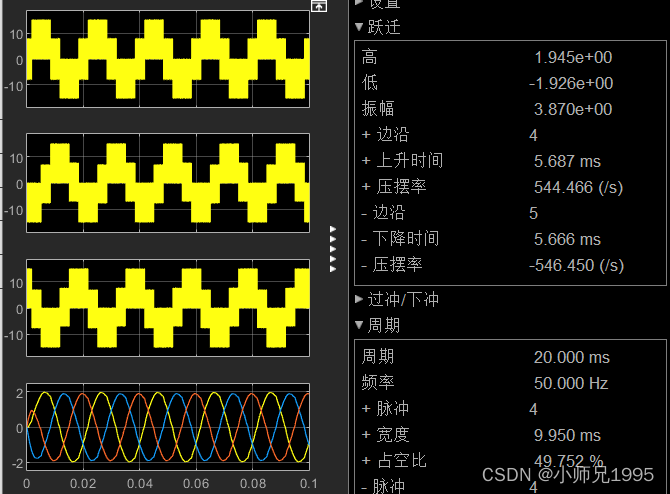
三相相电流及滤波后的三相相电流波形:
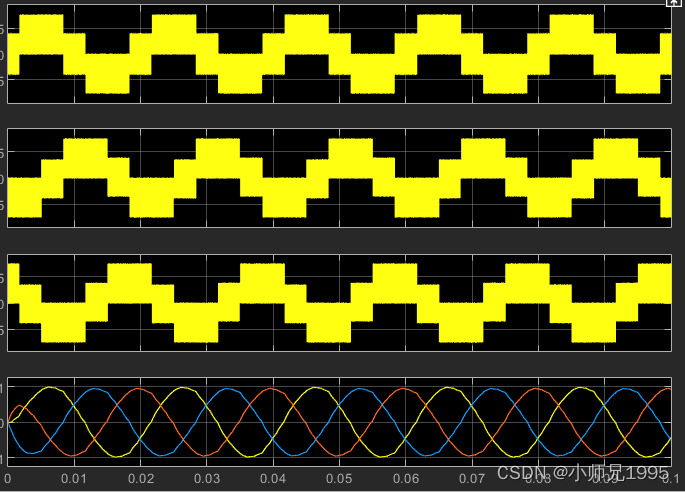
三相线电压及滤波后的三相线电压波形:
九、五段式SVPWM仿真分析
与上述7段式SVPWM算法的不同点就是,算法扇区切换点的时间不同,算法改动如下,其余部分同上述7段式SVPWM算法仿真。
function [Tcm1,Tcm2,Tcm3,sector] = SVPWM(Valpha,Vbeta,Udc,Tpwm,ARR)
%输出变量初始化
Tcm1 = 0;
Tcm2 = 0;
Tcm3 = 0;
sector = 0;
%扇区计算
%N与扇区对应的关系
% 3 1 5 4 6 2
% I II III IV V VI
Vref1 = Vbeta;
Vref2 = (sqrt(3)*Valpha-Vbeta)/2;
Vref3 = (-sqrt(3)*Valpha-Vbeta)/2;
if(Vref1>0)
sector = 1;
end
if(Vref2>0)
sector = sector+2;
end
if(Vref3>0)
sector = sector+4;
end
%扇区内合成矢量作用时间计算
X = sqrt(3)*Vbeta*Tpwm/Udc;
Y = Tpwm/Udc*(3/2*Valpha+sqrt(3)/2*Vbeta);
Z = Tpwm/Udc*(-3/2*Valpha+sqrt(3)/2*Vbeta);
switch(sector)
case 1
T1 = Z;T2 = Y;
case 2
T1 = Y;T2 = -X;
case 3
T1 = -Z;T2 = X;
case 4
T1 = -X;T2 = Z;
case 5
T1 = X;T2 = -Y;
otherwise
T1 = -Y;T2 = -Z;
end
%过调制处理
if(T1+T2>Tpwm)
T1 = Tpwm*T1/(T1+T2);
T2 = Tpwm*T2/(T1+T2);
else
T1 = T1;
T2 = T2;
end
%扇区内合成矢量切换点时间计算
%此处为5段式SVPWM切换点时间计算
ta = 0;
tb = ta+T1/2;
tc = tb+T2/2;
%输出调制信号
switch(sector)
case 1
Tcm1 = tb;
Tcm2 = ta;
Tcm3 = tc;
case 2
Tcm1 = ta;
Tcm2 = tc;
Tcm3 = tb;
case 3
Tcm1 = ta;
Tcm2 = tb;
Tcm3 = tc;
case 4
Tcm1 = tc;
Tcm2 = tb;
Tcm3 = ta;
case 5
Tcm1 = tc;
Tcm2 = ta;
Tcm3 = tb;
case 6
Tcm1 = tb;
Tcm2 = tc;
Tcm3 = ta;
end
%调制信号处理,生成输入到MCU中的调制信号
Tcm1 = 2*Tcm1/Tpwm;
Tcm2 = 2*Tcm2/Tpwm;
Tcm3 = 2*Tcm3/Tpwm;
Tcm1 = Tcm1*ARR;
Tcm2 = Tcm2*ARR;
Tcm3 = Tcm3*ARR;
end
9.1.仿真结果分析
电压空间矢量的运动轨迹:

扇区判断结果:
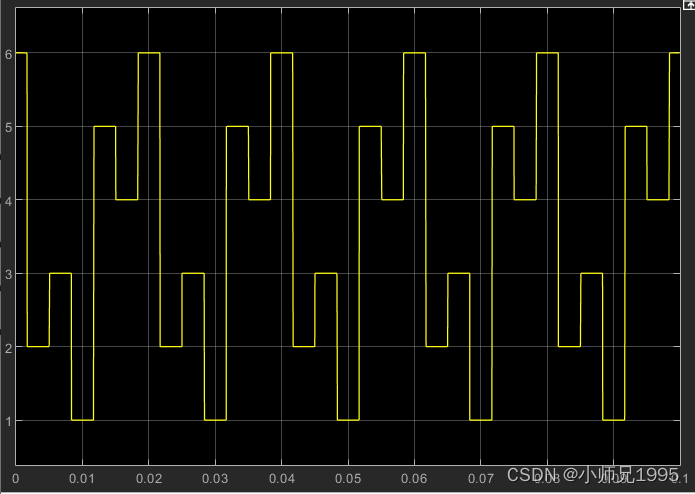
扇区内矢量切换点,即调制波波形:
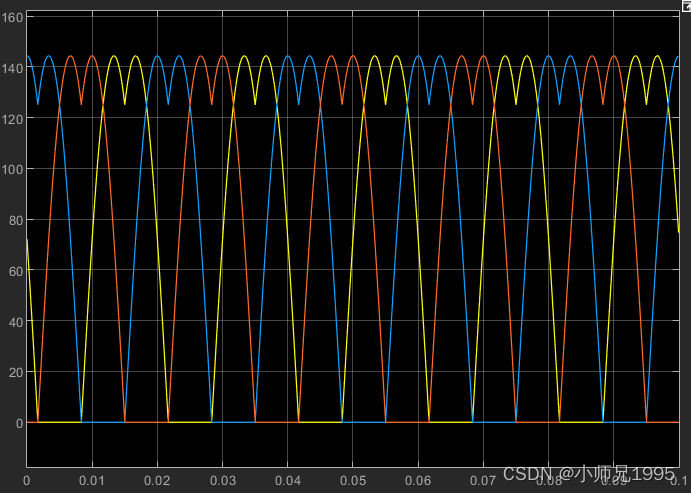
PWM信号:
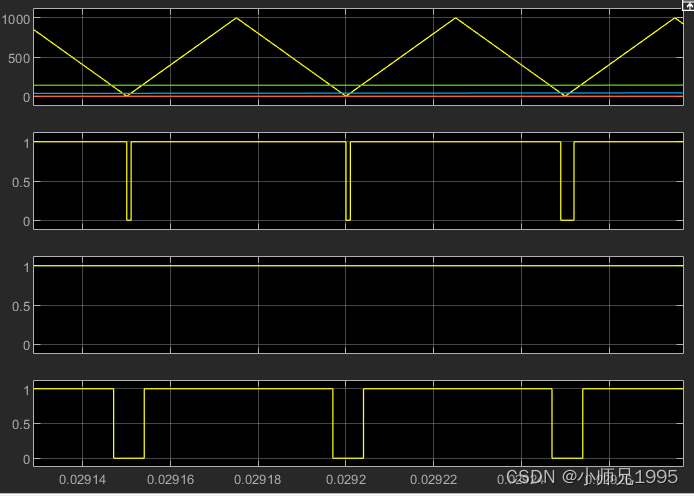
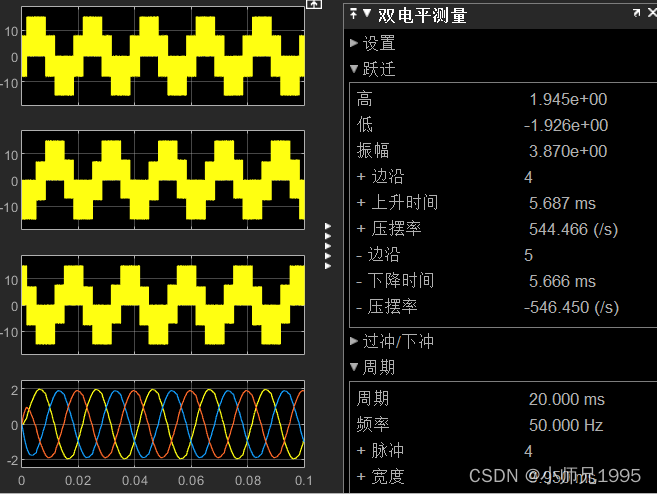
三相相电压及滤波后的三相相电压波形:生成的三相正弦电压与期望的输入电压参数一致,幅值为2,频率为50Hz。

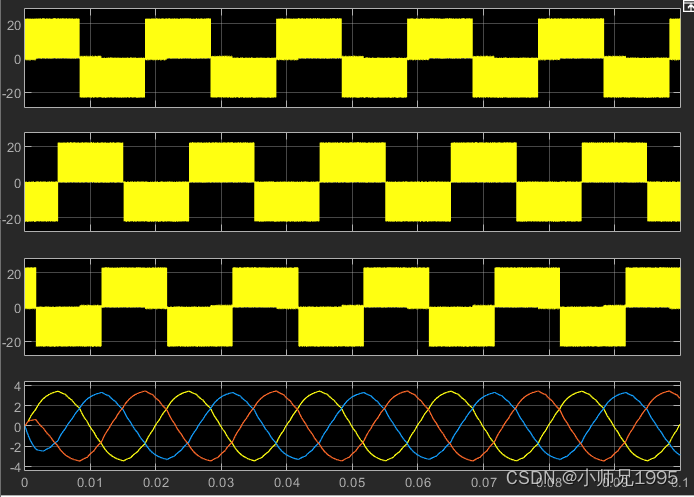
三相相电流及滤波后的三相相电流波形:

三相线电压及滤波后的三相线电压波形:
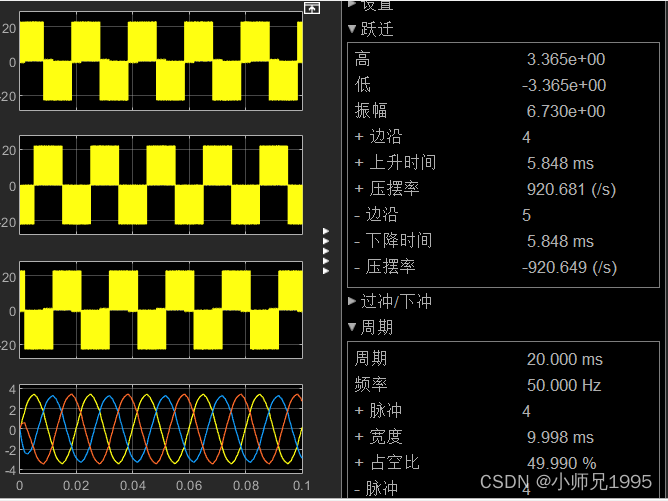
十、PMSM电压开环控制Matlab/Simulink仿真分析
有关永磁同步电机电压开环控制的原理请阅读:
永磁同步电机(PMSM)磁场定向控制(FOC)及Matlab/Simulink仿真分析
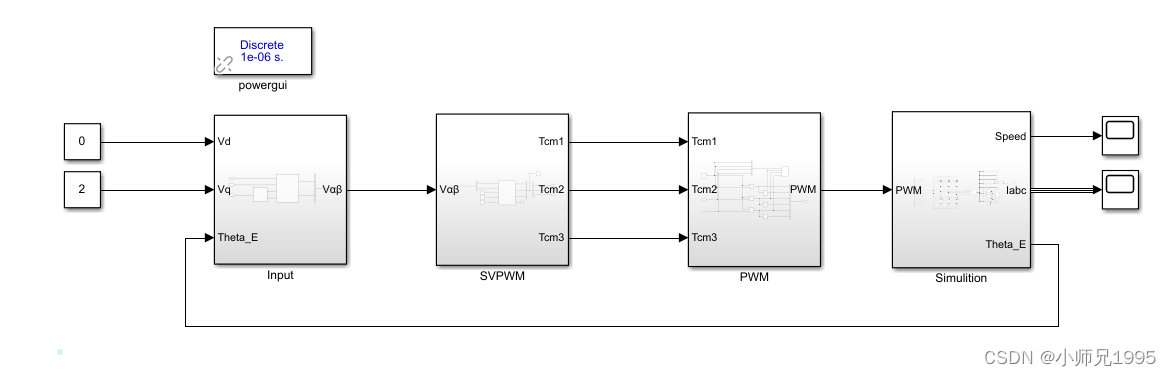
10.1.仿真电路分析
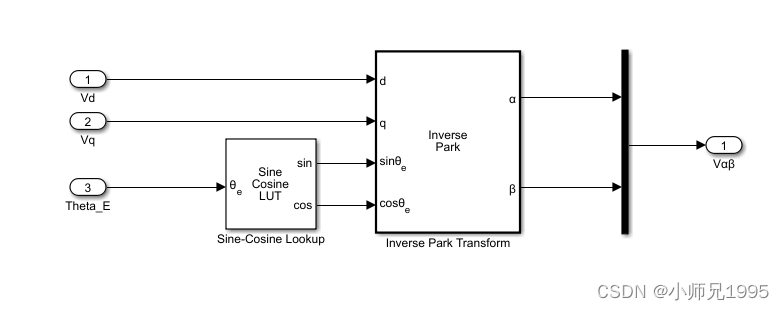
直接给定同步旋转坐标系下Vd,Vq的电压值实现永磁同步电机磁场定向的电压开环控制。
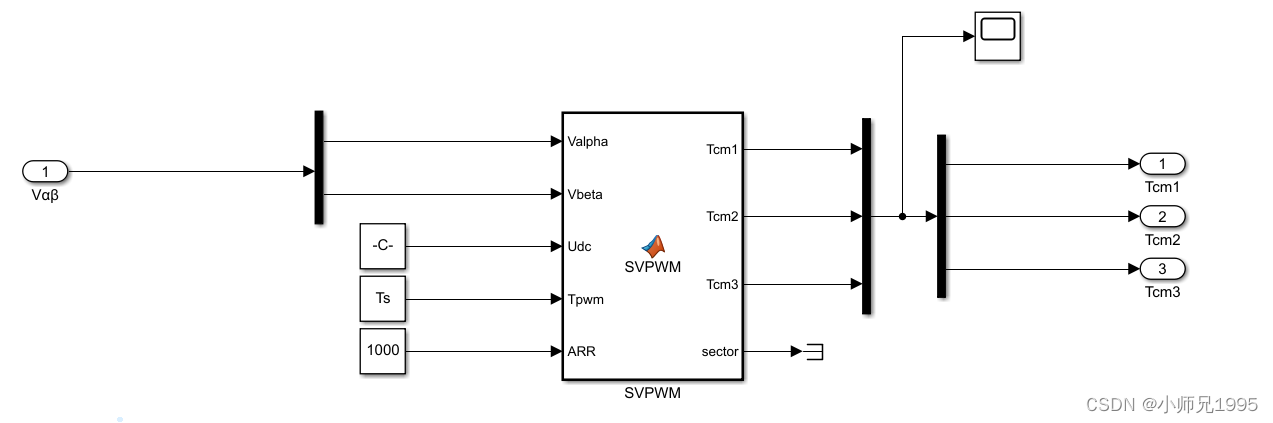
7段式SVPWM算法
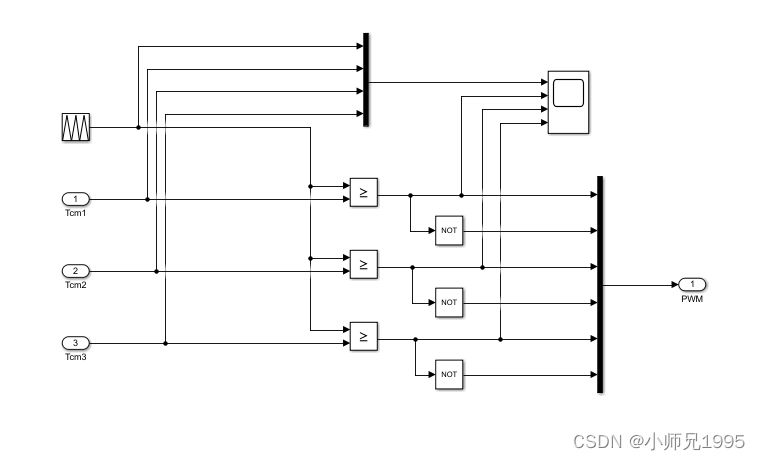
PWM控制信号生成
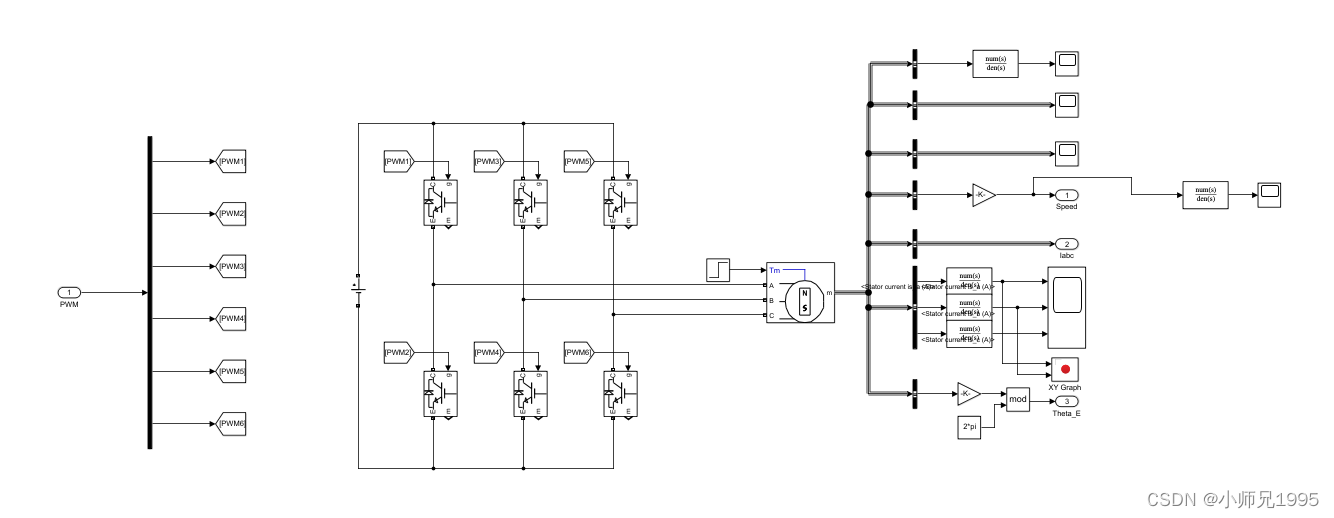
三相逆变电路及永磁同步电机,电机参数如下:

10.2.仿真结果分析
电压空间矢量的运动轨迹:
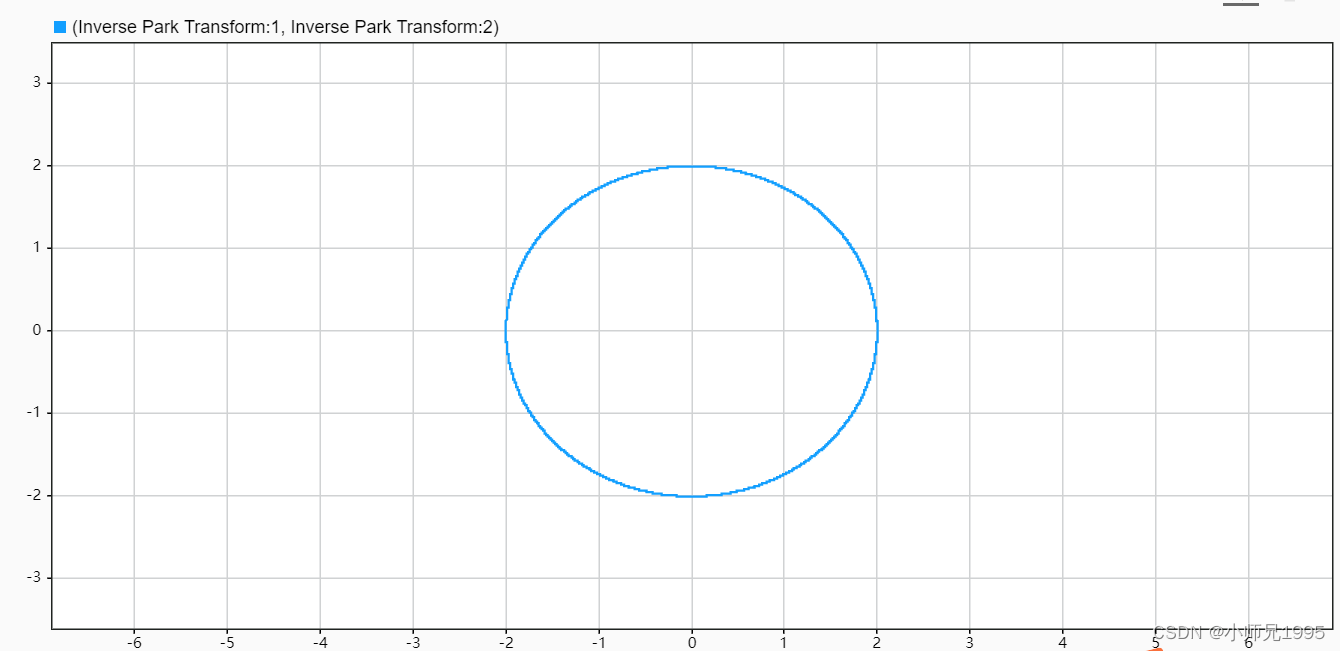
扇区内矢量切换点,即调制波波形:
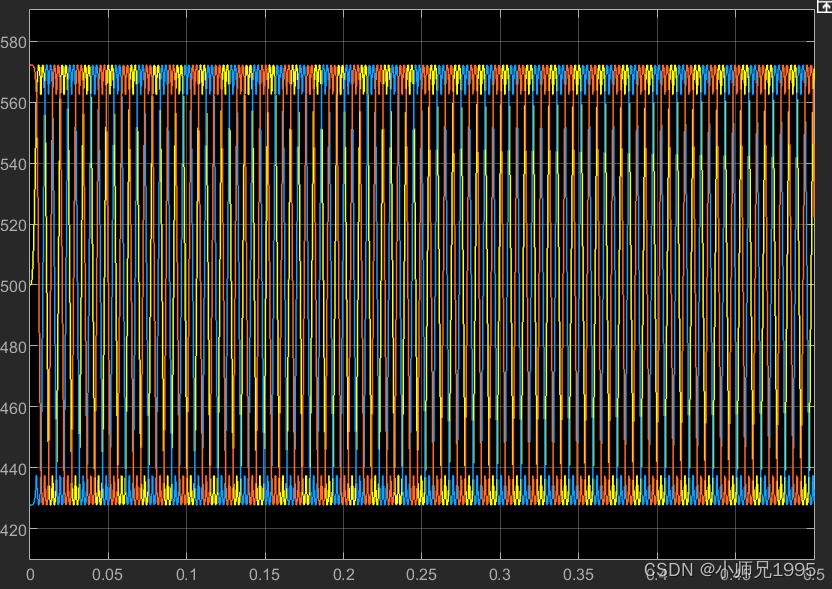
PWM信号:
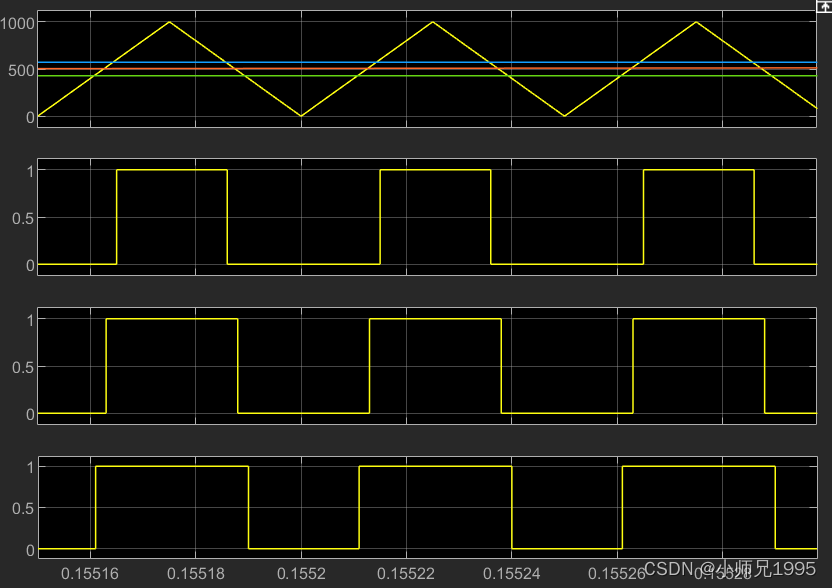
电机转速:
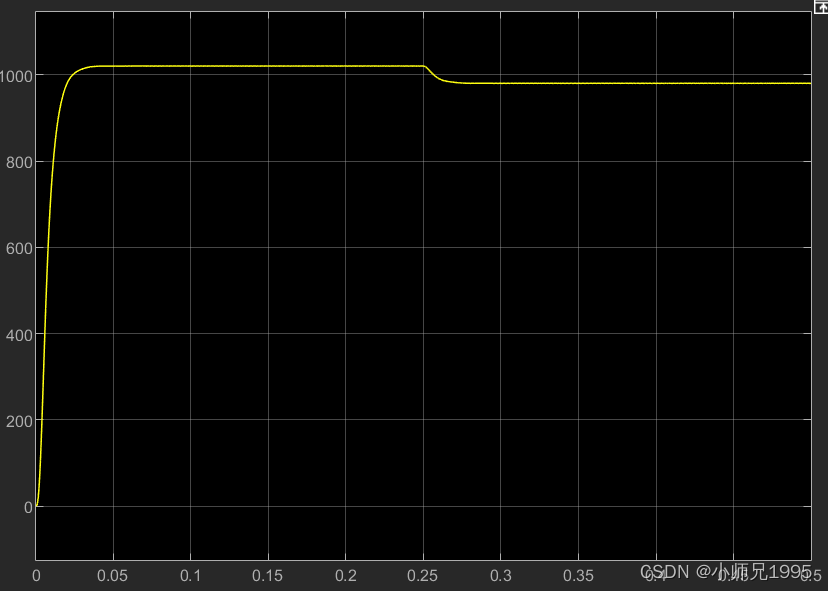
定子电流未滤波和滤波后的电流:
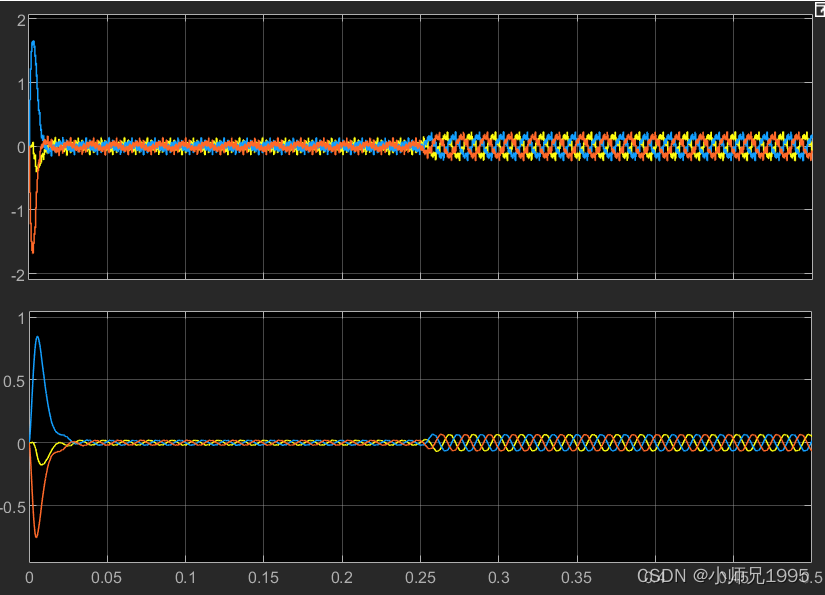
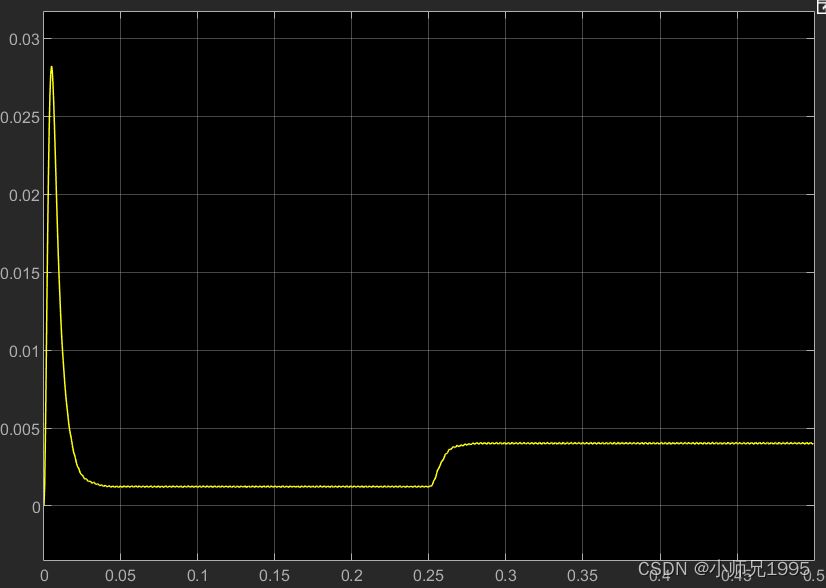
同步旋转坐标系下的定子电流Id、Iq,未滤波和滤波后的电流:
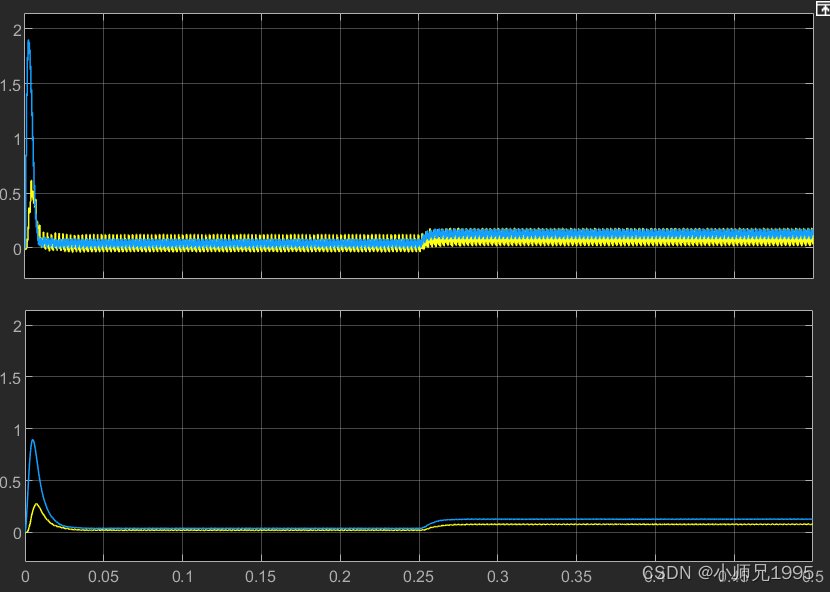
同步旋转坐标系下的定子电压Vd、Vq,未滤波和滤波后的电压:
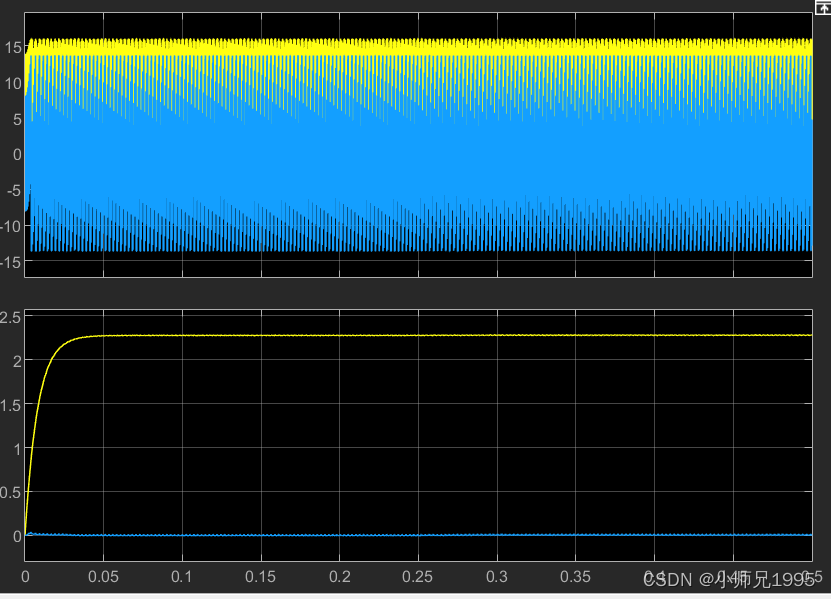
电磁转矩:
总结
本章节首先介绍了SVPWM控制技术的原理,然后详细分析了SVPWM控制算法的具体实现方式,并通过Matlab/Simulink对SVPWM控制算法进行了仿真分析,最后通过永磁同步电机矢量控制的实例进行了算法实现,为后续章节的分析奠定基础。
模型及代码工程获取: