特征提取是滚动轴承故障诊断及状态监测的关键,直接关系到轴承状态预示及故障识别的准确性,也是轴承故障诊断中的研究热点。考虑到轴承故障冲击会导致振动信号的形态改变,进而引起相关统计参数的变化,所以通过振动信号计算的统计量可以作为反映轴承运行状态的特征,应用比较广泛的有:峭度值、均方根值、峰峰值、熵、稀疏值、波峰因数、平滑指数、斜度值、分形维数等等。除了以上介绍的统计量特征外,频域和时频域分析方法在滚动轴承故障冲击信号处理及特征提取中的应用也非常广泛,功率谱分析、高阶谱技术、倒谱分析等方法能够获取滚动轴承故障冲击信号的频域特征,而短时傅立叶变换、连续小波变换、Wigner-Ville 分布、经验模态分解等方法则可以计算得到轴承故障冲击信号的时频域特征。
虽然上述方法可以获得多种表征轴承运行状态的特征,但轴承故障冲击信号最具代表性的特征是特征频率分量,在轴承故障诊断中的应用也最为广泛,通过检查信号中的特征频率分量能够对轴承是否存在缺陷以及缺陷位置同时作出判断。包络谱分析可以有效地提取出轴承故障冲击信号的特征频率分量,但是容易受到干扰成分及噪声的影响,要结合窄带分析方法来提高表现效果。窄带信号分析方法即共振解调技术,在滚动轴承故障振动信号分析中应用广泛,具体实施过程包括以下几步:首先借助事先定义的准则确定信号共振频带,再通过带通滤波器提取出最优窄频带信号,最后进行希尔伯特变换解调出包络信号,依靠包络信号中的主要频率成分确定轴承故障类别。窄带信号分析方法的要点在于确定有效的共振频带,相关研究主要集中在窄频带划分及频带确定准则参数计算两个方面。
窄带信号分析方法中最知名的是峭度图方法,其将谱峭度作为短时傅里叶变换窗口宽度的函数,用于定位振动信号中的敏感故障频带,在滚动轴承故障诊断中取得了非常好的效果。为了降低计算时间,快速峭度图方法被提出,甚至能够用于机械故障的在线检测。
窄带信号分析方法依靠带通滤波器滤除了窄频带外的干扰分量,从而能专注于窄带内信号的分析,非常适用于强噪声、大干扰情况下滚动轴承微弱冲击信号的特征提取,只是最优频带的选择非常具有挑战性和不确定性,极容易受到带内噪声、独立频率分量、准周期冲击分量等干扰成分的影响。鉴于此,采用一种基于优化信息频带的旋转机械故障诊断方法对滚动轴承进行故障诊断,运行环境为MATLAB R2018A。
while iter <= Nit
% fprintf(['Iteration:' num2str(iter) '\n'])
% forward operator
% x = x - mu * (A^T(A(x) - y))
tmp = x;
AHAx = AH(Ax);
for i = 1:numel(tmp)
tmp{i} = tmp{i} + mu * ( AHy{i} - AHAx{i} );
end
% backward (thresholding) with K-sparsity
Temp = [];
for i = 1: J+1
Temp = [Temp ; tmp{i}(:) / normA(i) / Weight(i)];
end
T = K_sparsity(Temp, K_s);
for i = 1: numel(x)
switch shrinkage
case 'half'
x{i} = half(tmp{i}, T * normA(i) * Weight(i));
case 'soft'
x{i} = soft(tmp{i}, T * normA(i) * Weight(i));
otherwise
error('Undefined shrinkage.')
end
end
Ax = A(x);
% cost function history
cost(iter) = 0.5 * norm(y(:)-Ax(:))^2 ;
stop = 0;
total = 0;
for i = 1: J+1
switch shrinkage
case 'half'
cost(iter) = cost(iter) + Weight(i) * sum(abs(x{i}(:)).^0.5);
case 'soft'
cost(iter) = cost(iter) + Weight(i) * sum(abs(x{i}(:)));
end
stop = stop + sum((x{i} - x_old{i}).^2);
total = total + sum((x{i}).^2);
end
% checkpoint
if sqrt(stop) / sqrt(total) < 1e-6
break;
end
iter = iter + 1;
x_old = x;
知乎学术咨询获取代码:
https://www.zhihu.com/consult/people/792359672131756032?isMe=1
end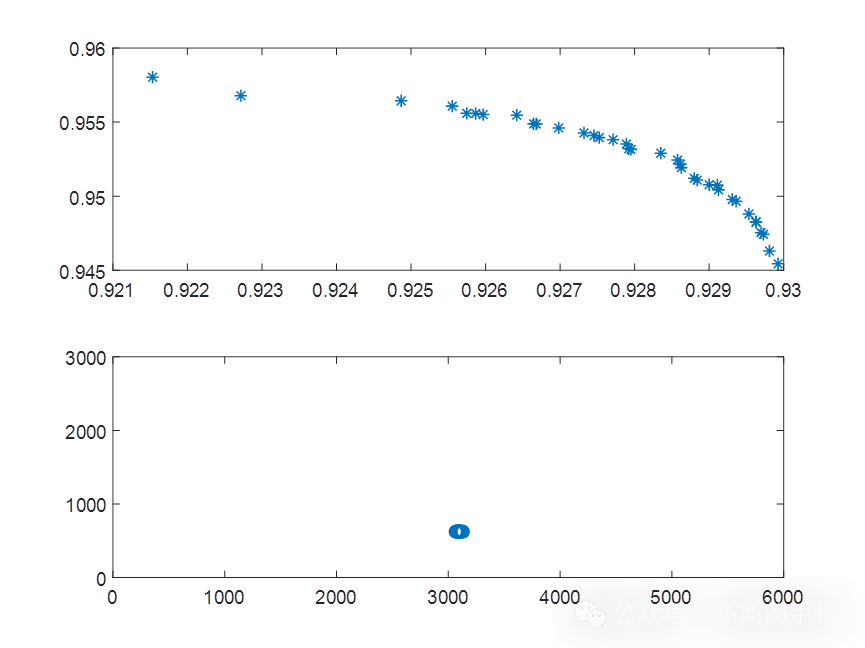
- 擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。