

🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础
💫个人格言: "如无必要,勿增实体"

文章目录
- K-means++: 一种改进的聚类算法详解
- 引言
- 1. K-means算法回顾
- 1.1 基本概念
- 1.2 局限性
- 2. K-means++算法介绍
- 2.1 初始质心选择策略
- 2.2 算法优势
- 3. K-means++算法实现步骤
- 3.1 准备工作
- 3.2 初始化质心
- 3.3 迭代优化
- 3.4 结果评估
- 4. 实际应用案例
- 4.1 数据降维
- 4.2 客户细分
- 4.3 文档分类
- 5. 总结
K-means++: 一种改进的聚类算法详解
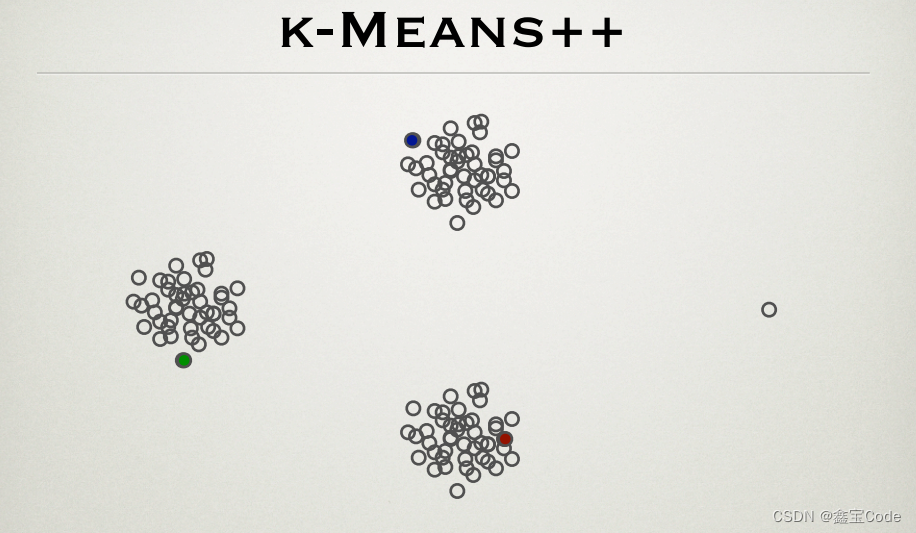
引言
在数据分析与机器学习领域,聚类算法作为无监督学习的重要组成部分,被广泛应用于数据分组、模式识别和数据挖掘等场景。其中,K-means算法以其简单直观和高效的特点,成为最常用的聚类方法之一。然而,经典K-means算法在初始聚类中心的选择上存在随机性,可能导致算法陷入局部最优解。为解决这一问题,2007年,David Arthur 和 Sergei Vassilvitskii 提出了K-means++算法,它通过一种智能化的初始化策略显著提高了聚类质量。本文将深入探讨K-means++算法的原理、优势、实现步骤以及实际应用案例,旨在为读者提供一个全面且易于理解的K-means++算法指南。
1. K-means算法回顾

1.1 基本概念
K-means算法的目标是将数据集划分为K个簇(clusters),每个簇由距离其质心(centroid)最近的数据点组成。算法迭代执行以下两个步骤直至收敛:
- 分配步骤:将每个数据点分配给最近的质心。
- 更新步骤:重新计算每个簇的质心,即该簇所有点的均值。
1.2 局限性
- 对初始质心敏感:随机选择的初始质心可能导致算法陷入局部最优解。
- 不适合处理不规则形状的簇:倾向于形成球形或凸形簇。
- 难以处理大小和密度变化较大的簇。
2. K-means++算法介绍
2.1 初始质心选择策略
K-means++算法的核心改进在于其初始化过程,具体步骤如下:
- 从数据集中随机选择第一个质心。
- 对于每个数据点
x,计算其到已选择的所有质心的最短距离D(x)。 - 选择一个新的数据点作为下一个质心,选择的概率与
D(x)成正比,即概率P(x)=D(x)/ ΣD(x)。 - 重复步骤2和3,直到选择了K个质心。
这种选择策略确保了质心之间的分散性,从而提高了聚类效果。
2.2 算法优势
- 减少局部最优解的风险:更大概率选择相距较远的初始质心,提高聚类质量。
- 理论保证:K-means++能够给出接近最优解的界,即与最优聚类方案的距离平方误差最多是理论最小值的8倍。
- 效率:虽然初始化复杂度有所增加,但整体算法依然保持高效,尤其是对于大规模数据集。
3. K-means++算法实现步骤
3.1 准备工作
- 确定K值:根据实际需求预先设定簇的数量。
- 数据预处理:标准化或归一化数据,以消除量纲影响。
3.2 初始化质心
- 按照K-means++策略选取K个初始质心。
3.3 迭代优化
- 分配数据点:将每个数据点分配给最近的质心。
- 更新质心:根据新分配结果,重新计算每个簇的质心。
- 检查收敛:如果质心位置变化不大于预定阈值或达到最大迭代次数,则停止迭代。
3.4 结果评估
- 使用如轮廓系数、Calinski-Harabasz指数等评价指标评估聚类质量
下面是一个使用Python和scikit-learn库实现K-means++算法的示例代码。首先,确保你已经安装了scikit-learn库,如果没有安装,可以通过运行pip install scikit-learn来安装。代码仅供参考
# 导入所需库
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# 生成模拟数据
# 这里我们创建一个包含3个类别的数据集,每个类别有不同数量的点和方差
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=[1.0, 1.5, 0.5], random_state=42)
# 使用KMeans++算法进行聚类
kmeans_plus = KMeans(n_clusters=3, init='k-means++', random_state=42) # 'k-means++' 是关键参数
kmeans_plus.fit(X)
# 可视化结果
plt.figure(figsize=(10, 5))
# 绘制原始数据点
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], c='grey')
plt.title('Original Data')
# 绘制K-means++聚类结果
plt.subplot(1, 2, 2)
plt.scatter(X[:, 0], X[:, 1], c=kmeans_plus.labels_, cmap='viridis')
plt.scatter(kmeans_plus.cluster_centers_[:, 0], kmeans_plus.cluster_centers_[:, 1], s=300, c='red', label='Centroids')
plt.title('K-means++ Clustering Result')
plt.legend()
plt.show()
这段代码首先生成了一个具有三个聚类中心的二维模拟数据集,然后使用scikit-learn的KMeans类,并设置init='k-means++'来应用K-means++初始化策略进行聚类。最后,通过matplotlib库可视化了原始数据点和聚类后的结果,其中红色点表示各个簇的质心。这个例子简洁地展示了如何在Python中实施K-means++算法并评估其效果。
4. 实际应用案例
4.1 数据降维
- 在PCA(主成分分析)之前,使用K-means++进行初步聚类,可以有效降低数据维度,提高后续分析效率。
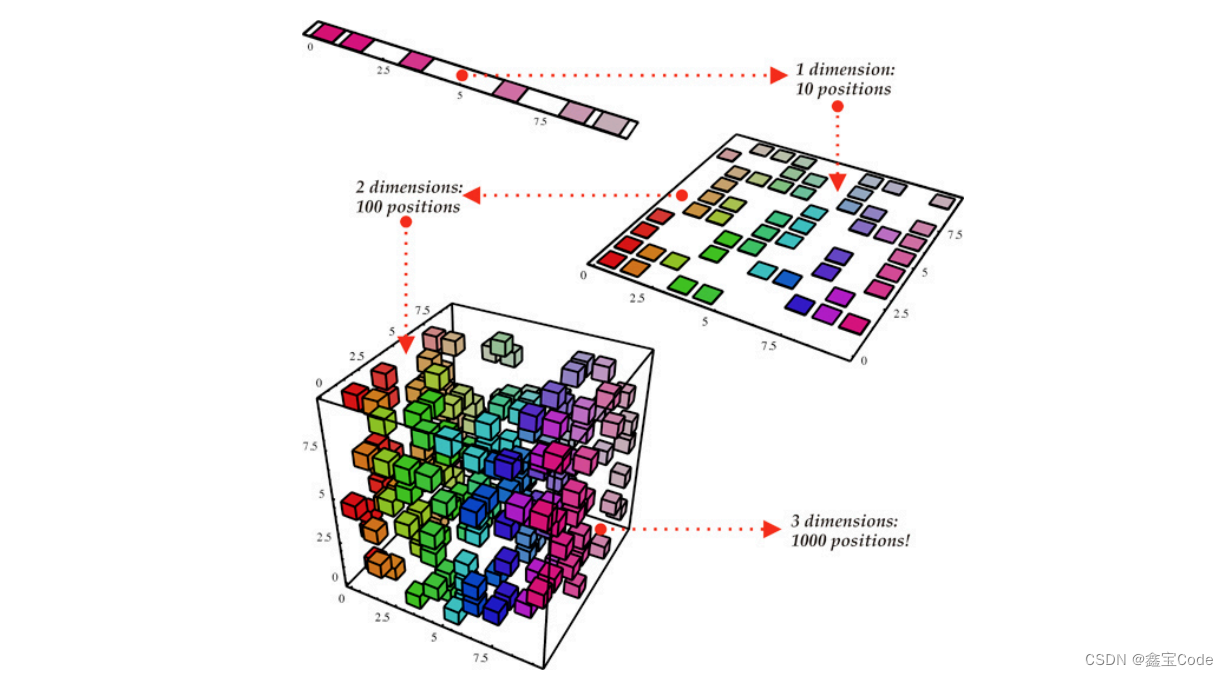
4.2 客户细分
- 在市场营销中,通过对客户消费行为数据进行K-means++聚类,企业可以识别不同的客户群体,定制个性化营销策略。
4.3 文档分类
- 在文本挖掘领域,利用K-means++对文档向量化后的特征进行聚类,有助于自动分类和主题发现。
5. 总结
K-means++算法通过一种更加智能的初始化策略,显著改善了经典K-means算法的性能,尤其在解决初始质心选择的随机性和局部最优问题上表现出色。它不仅在理论上提供了性能保证,而且在实践中广泛应用于多个领域,展现了强大的实用价值。随着大数据和机器学习技术的发展,K-means++及其变种将继续在数据科学中扮演重要角色。















![[leetcode]first-unique-character-in-a-string 字符串中的第一个唯一字符](https://img-blog.csdnimg.cn/direct/610caa47a71b4fe4ad6854dc436e0e9c.png)
