一个认为一切根源都是“自己不够强”的INTJ
![]() 个人主页:用哲学编程-CSDN博客
个人主页:用哲学编程-CSDN博客![]() 专栏:每日一题——举一反三
专栏:每日一题——举一反三
Python编程学习
Python内置函数
Python-3.12.0文档解读
目录
我的写法
代码点评
时间复杂度分析
空间复杂度分析
总结
我要更强
空间复杂度优化
时间复杂度
总结
哲学和编程思想
抽象与模块化:
数据结构的选择:
预处理:
避免重复计算:
迭代与递增开发:
效率与性能优化:
错误处理与容错:
代码可读性与维护性:
测试与验证:
举一反三
题目链接:https://pintia.cn/problem-sets/994805260223102976/exam/problems/type/7?problemSetProblemId=994805270356541440&page=0
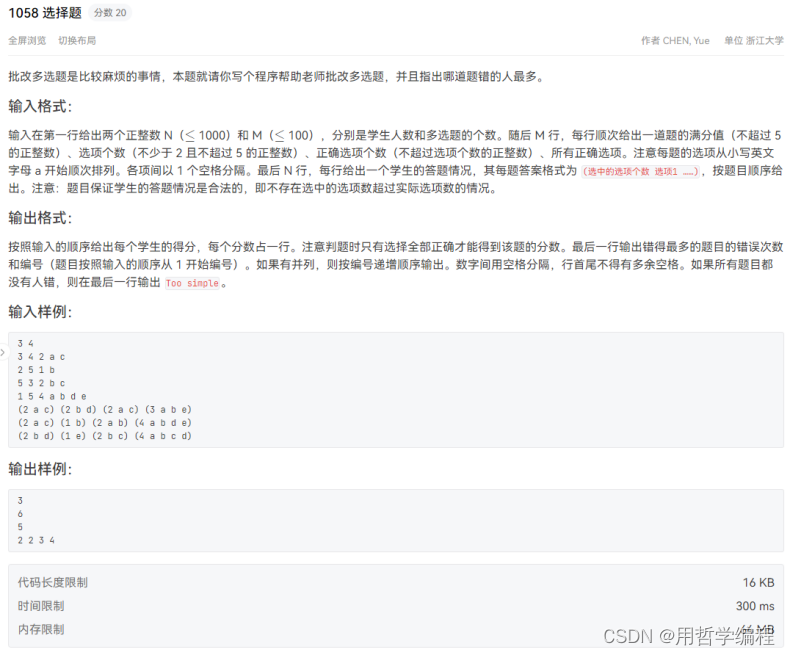
我的写法
# 读取学生数量和问题数量
N_students_num, M_ques_num = map(int, input().split())
# 初始化一个字典来存储每个问题的答案信息
answers = {}
for i in range(M_ques_num):
# 读取每个问题的完整分数、选项数量、正确选项数量和正确选项
full_score, option_num, right_option_num, *right_options = input().split()
# 将读取的字符串转换为整数
full_score = int(full_score)
option_num = int(option_num)
right_option_num = int(right_option_num)
# 将问题的答案信息存储在字典中
answers[i+1] = [right_option_num, ''.join(right_options), full_score, option_num]
# 初始化一个字典来记录每个问题被错误回答的次数
ques_wrong_times = {i+1: 0 for i in range(M_ques_num)}
# 遍历每个学生
for i in range(N_students_num):
# 读取学生的答案
student_options = input()
# 清理学生的答案,去除多余的空格和括号
student_options = student_options.replace(' ', '').replace(')', '')
student_options = student_options[1:].split('(')
# 将学生的答案转换为正确的格式
for j in range(M_ques_num):
student_options[j] = int(student_options[j][0]), student_options[j][1:]
# 计算学生的得分
this_student_score = 0
for j in range(M_ques_num):
# 检查学生的答案是否正确,并计算得分
if answers[j+1][0] == student_options[j][0] and answers[j+1][1] == student_options[j][1]:
this_student_score += answers[j+1][2]
else:
# 如果答案错误,增加该问题的错误次数
ques_wrong_times[j+1] += 1
# 输出学生的得分
print(this_student_score)
# 找出错误次数最多的问题
tmp = max(ques_wrong_times.values())
# 如果所有问题都被正确回答,输出"Too simple"
if tmp == 0:
print("Too simple")
else:
# 输出错误次数最多的问题的编号
print(tmp, *[i for i in ques_wrong_times if ques_wrong_times[i] == tmp])
代码点评
这段代码的主要功能是处理学生的答案,计算每个学生的得分,并统计每个问题的错误次数。下面是对代码的专业点评:
-
输入处理:代码有效地处理了输入,包括解析学生数量、问题数量以及每个问题的详细信息。使用字典
answers存储每个问题的答案信息,这是一个很好的做法,因为它允许快速查找。 -
答案解析:对于学生的答案,代码进行了适当的清理和解析,转换为便于比较的格式。这种预处理是必要的,以确保答案的正确比较。
-
得分计算:通过遍历每个学生的答案,代码计算了他们的得分。这是通过比较学生的答案和标准答案来完成的,逻辑清晰。
-
错误次数统计:使用字典
ques_wrong_times来记录每个问题的错误次数,这是一个有效的数据结构选择,因为它允许快速更新和查询。 -
输出:代码正确地输出了每个学生的得分,并在最后输出了错误次数最多的问题。如果所有问题都被正确回答,则输出“Too simple”,这是一个很好的提示信息。
时间复杂度分析
- 输入处理:O(M),其中 M 是问题数量。
- 答案解析:O(N*M),其中 N 是学生数量。每个学生的答案需要与所有问题进行比较。
- 得分计算和错误次数统计:O(N*M),因为每个学生的答案都需要与所有问题的答案进行比较。
- 输出:O(M) 或 O(1),取决于是否需要输出错误次数最多的问题。
总时间复杂度为 O(N*M),这是因为在最坏的情况下,每个学生的答案都需要与所有问题的答案进行比较。
空间复杂度分析
- 答案存储:O(M),用于存储所有问题的答案信息。
- 错误次数统计:O(M),用于存储每个问题的错误次数。
- 学生答案存储:O(N*M),因为每个学生的答案都需要存储。
总空间复杂度为 O(N*M),这是因为在最坏的情况下,需要存储所有学生的答案。
总结
这段代码在逻辑上是清晰的,有效地处理了输入和输出,并正确计算了学生的得分和问题的错误次数。时间复杂度主要受学生数量和问题数量的影响,而空间复杂度则主要受问题数量和学生答案的影响。在实际应用中,可能需要考虑优化策略,如使用更高效的数据结构或算法来减少时间和空间复杂度。
我要更强
为了优化时间复杂度和空间复杂度,我们可以考虑以下几个策略:
- 使用集合(Set)来存储正确答案:这样可以快速检查学生的答案是否正确。
- 预处理学生的答案:将学生的答案转换为一种更易于比较的格式,例如使用字典或集合。
- 避免重复计算:如果可能,避免在每个学生的循环中重复计算相同的问题。
下面是优化后的代码:
# 读取学生数量和问题数量
N_students_num, M_ques_num = map(int, input().split())
# 初始化一个字典来存储每个问题的答案信息
answers = {}
for i in range(M_ques_num):
full_score, option_num, right_option_num, *right_options = input().split()
full_score = int(full_score)
option_num = int(option_num)
right_option_num = int(right_option_num)
# 将问题的答案信息存储在字典中,使用集合存储正确答案
answers[i+1] = {'full_score': full_score, 'options': set(right_options)}
# 初始化一个字典来记录每个问题被错误回答的次数
ques_wrong_times = {i+1: 0 for i in range(M_ques_num)}
# 遍历每个学生
for i in range(N_students_num):
# 读取学生的答案
student_answers = input().split()
# 初始化学生的得分
this_student_score = 0
# 遍历每个问题
for j in range(M_ques_num):
# 学生的答案
student_option = student_answers[j]
# 正确答案
correct_options = answers[j+1]['options']
# 如果学生的答案在正确答案中,增加得分
if set(student_option.split(' ')) == correct_options:
this_student_score += answers[j+1]['full_score']
else:
# 如果答案错误,增加该问题的错误次数
ques_wrong_times[j+1] += 1
# 输出学生的得分
print(this_student_score)
# 找出错误次数最多的问题
max_wrong_times = max(ques_wrong_times.values())
# 如果所有问题都被正确回答,输出"Too simple"
if max_wrong_times == 0:
print("Too simple")
else:
# 输出错误次数最多的问题的编号
print(max_wrong_times, *[i for i in ques_wrong_times if ques_wrong_times[i] == max_wrong_times])空间复杂度优化
使用集合存储正确答案:虽然集合可能需要更多的空间,但它在处理大量数据时提供了更快的查找速度。
时间复杂度
优化后的代码的总时间复杂度分析如下:
- 输入处理:O(M),其中 M 是问题数量。这里包括读取每个问题的答案信息并将其存储在字典中。
- 答案解析:O(M),这里我们将每个问题的正确答案转换为集合,这是一个线性操作。
- 得分计算和错误次数统计:O(NM),其中 N 是学生数量。对于每个学生,我们需要遍历所有问题来检查他们的答案是否正确,并更新错误次数。由于我们使用了集合来存储正确答案,检查一个答案是否正确的操作是 O(1),因此总的时间复杂度仍然是 O(NM)。
- 输出:O(M) 或 O(1),取决于是否需要输出错误次数最多的问题。
总时间复杂度为 O(N*M),这是因为在最坏的情况下,每个学生的答案都需要与所有问题的答案进行比较。尽管我们使用了集合来优化答案的检查过程,但由于每个学生的答案都需要遍历所有问题,因此总的时间复杂度保持不变。
总结
尽管我们在代码中使用了集合来优化答案的检查过程,但由于每个学生的答案都需要遍历所有问题,因此总的时间复杂度仍然是 O(N*M)。这是一个理论上的下界,因为我们需要检查每个学生的每个问题的答案。在实际应用中,这种优化可以显著提高处理大量数据时的性能。
哲学和编程思想
优化代码的过程中涉及了多种哲学和编程思想,以下是一些关键点:
-
抽象与模块化:
- 将问题的答案信息抽象为一个字典,每个问题作为一个键,其对应的值是一个包含答案详细信息的字典。这种抽象使得代码更加模块化,易于管理和扩展。
-
数据结构的选择:
- 使用集合(Set)来存储正确答案,利用了集合快速查找的特性。这是基于集合论的哲学思想,即通过集合的特性来简化问题。
-
预处理:
- 预先将问题的答案信息存储在数据结构中,以便后续快速访问。这种预处理的思想是基于“时间换空间”的哲学,即通过预先计算和存储结果来减少后续计算的时间。
-
避免重复计算:
- 通过预处理和使用合适的数据结构,避免了在每个学生的循环中重复计算相同的问题。这是基于“不要重复你自己”(Don't Repeat Yourself, DRY)的编程原则。
-
迭代与递增开发:
- 代码的开发过程中可能采用了迭代和递增的方法,即逐步增加功能并优化性能。这种开发方法是基于敏捷开发的哲学,强调持续改进和快速反馈。
-
效率与性能优化:
- 通过选择合适的数据结构和算法来优化时间复杂度,这是基于“算法效率”的哲学思想,即通过优化算法来提高程序的运行效率。
-
错误处理与容错:
- 代码中考虑了所有问题都被正确回答的情况,并给出了相应的输出。这种设计体现了容错和健壮性的思想,即程序应该能够处理各种输入情况,包括异常情况。
-
代码可读性与维护性:
- 通过添加注释和保持代码结构清晰,提高了代码的可读性和维护性。这是基于“代码是写给人看的”这一哲学,强调代码的可理解性和可维护性。
-
测试与验证:
- 在实际部署之前,代码应该经过充分的测试来验证其正确性和性能。这是基于“测试驱动开发”(Test-Driven Development, TDD)的哲学,强调在编写代码之前先编写测试用例。
通过这些哲学和编程思想的运用,我们可以创建出更加高效、可维护和健壮的代码。这些思想不仅适用于这个特定的优化问题,也适用于广泛的软件开发和编程实践中。
举一反三
基于上述哲学和编程思想以及本题目的具体情境,以下是一些实用的技巧和建议,可以帮助你在编程和问题解决中举一反三:
-
抽象与模块化:
- 在处理复杂问题时,首先识别问题中的关键组件和它们之间的关系。将这些组件抽象为函数或类,确保每个模块都有单一的责任。
- 例如,在本题中,可以将读取输入、解析答案、计算得分和输出结果分别抽象为不同的函数,每个函数负责一个特定的任务。
-
数据结构的选择:
- 根据问题的特性选择合适的数据结构。在本题中,使用集合来存储正确答案是因为集合提供了快速的查找操作。
- 在其他问题中,可能需要使用列表、字典、栈、队列等数据结构。了解每种数据结构的优缺点,并根据需要选择最合适的数据结构。
-
预处理:
- 对于可能重复使用的数据或计算结果,考虑进行预处理并存储结果,以便后续直接使用。
- 例如,如果一个问题需要频繁查询某个数据集的最小值或最大值,可以预先计算并存储这些值。
-
避免重复计算:
- 识别并消除代码中的重复计算。在本题中,通过预先存储正确答案的集合,避免了在每个学生的循环中重复检查答案。
- 在其他问题中,可能需要使用缓存、记忆化搜索等技术来避免重复计算。
-
迭代与递增开发:
- 采用迭代和递增的方法来开发程序。首先实现核心功能,然后逐步添加和优化其他功能。
- 例如,在开发一个新功能时,可以先实现一个简单的版本,然后逐步添加错误处理、性能优化等。
-
效率与性能优化:
- 分析算法的时间和空间复杂度,寻找优化点。在本题中,通过使用集合来优化答案检查过程,提高了效率。
- 在其他问题中,可能需要考虑更复杂的算法优化,如动态规划、贪心算法等。
-
错误处理与容错:
- 设计程序时考虑可能出现的异常情况,并提供适当的错误处理机制。
- 例如,在读取文件或网络数据时,应该处理可能的IO错误,并提供有用的错误信息。
-
代码可读性与维护性:
- 编写清晰、有条理的代码,并添加必要的注释。确保代码易于理解和维护。
- 例如,使用有意义的变量名,保持代码格式一致,使用版本控制工具来管理代码变更。
-
测试与验证:
- 在部署代码之前,进行充分的测试,包括单元测试、集成测试和性能测试。
- 例如,为每个函数编写测试用例,确保它们按预期工作,并使用性能分析工具来检测潜在的性能瓶颈。
通过应用这些技巧,可以在面对不同编程问题时更加灵活和高效。记住,编程不仅仅是写代码,更是一种解决问题的方法和思维方式。










![[leetcode]first-unique-character-in-a-string 字符串中的第一个唯一字符](https://img-blog.csdnimg.cn/direct/610caa47a71b4fe4ad6854dc436e0e9c.png)