前言
今天我们来聊聊题外话,量子纠缠,在目前物理分支中,要说最深,最能改变人类对宇宙影响的莫过于量子力学了,假如我们可以人为的对两个粒子施加纠缠态,那么我们将可以足不出户的完成对外界的操控
简介
量子纠缠(Quantum Entanglement)是量子力学中的一种现象,其中两个或多个粒子彼此之间存在某种关联,即使它们在空间上相隔甚远。这种关联是如此强大,以至于一个粒子的状态立即决定了其他粒子的状态,无论它们相距多远
基本概念
态矢量(State Vector):
在量子力学中,粒子的状态可以用一个态矢量来表示,通常记作 ∣𝜓⟩。
叠加态(Superposition State):
粒子的状态可以是多种状态的叠加,即 ∣𝜓⟩=𝛼∣0⟩+𝛽∣1⟩,其中
𝛼 和 𝛽 是复数,且 ∣𝛼∣2+∣𝛽∣2=1。
纠缠态(Entangled State):
纠缠态是一种特殊的量子态,其中两个或多个粒子的状态紧密关联。例如,两个量子比特的纠缠态可以表示为 ∣𝜓⟩=1/
2
\sqrt{2}
2(∣00⟩+∣11⟩)。
量子纠缠的特性
非局域性(Non-locality):
量子纠缠态的特性是非局域的,即纠缠粒子之间的关联不受空间距离的影响。即使将两个纠缠粒子分开很远,一个粒子的测量结果仍然会立即影响另一个粒子的状态。
EPR佯谬(EPR Paradox):
爱因斯坦、波多尔斯基和罗森提出的EPR佯谬质疑量子力学的完备性,认为量子力学不能完全描述物理现实。然而,量子纠缠通过实验证明了量子力学的非局域性和完备性。
贝尔不等式(Bell’s Inequality):
贝尔不等式是一种数学关系,用于测试量子力学的非局域性。实验表明,量子纠缠态违反了贝尔不等式,支持了量子力学的理论预测。
量子纠缠的应用
量子计算(Quantum Computing):
量子纠缠是量子计算的基础。通过纠缠态,可以实现量子比特的并行处理,极大地提高计算效率。
量子通信(Quantum Communication):
量子纠缠在量子密钥分发(如BB84协议)中起关键作用,确保通信的绝对安全性。
量子隐形传态(Quantum Teleportation):
通过量子纠缠,可以将粒子的量子态从一个地方传输到另一个地方,而无需传输实际的物质粒子。
总结
量子纠缠是量子力学中最神秘且最有趣的现象之一。它揭示了自然界中存在着深刻的关联,这种关联不仅在理论上极具吸引力,而且在实际应用中也具有巨大的潜力。量子纠缠不仅改变了我们对世界的理解,也正在推动量子技术的发展,为未来的科学和技术带来无限可能
本文代码
应用了Hadamard和CNOT门后的纠缠态密度矩阵
代码
% GHZ态
alpha = 1/sqrt(2);
beta = 1/sqrt(2);
ghz_state = [alpha; 0; 0; beta];
% W态
w_state = [1/sqrt(3); 1/sqrt(3); 1/sqrt(3); 0];
% 密度矩阵计算函数
function density_matrix = calculate_density_matrix(state)
density_matrix = state * state';
end
% 可视化密度矩阵函数
function visualize_density_matrix(density_matrix, title_text)
figure;
subplot(1, 2, 1);
imagesc(real(density_matrix));
colorbar;
title(['Real Part of ', title_text]);
xlabel('State Index');
ylabel('State Index');
axis square;
subplot(1, 2, 2);
imagesc(imag(density_matrix));
colorbar;
title(['Imaginary Part of ', title_text]);
xlabel('State Index');
ylabel('State Index');
axis square;
end
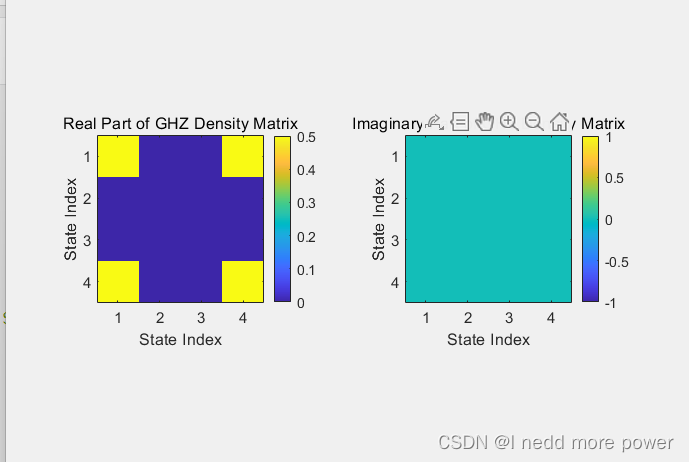
% 可视化GHZ态
ghz_density_matrix = calculate_density_matrix(ghz_state);
visualize_density_matrix(ghz_density_matrix, 'GHZ Density Matrix');
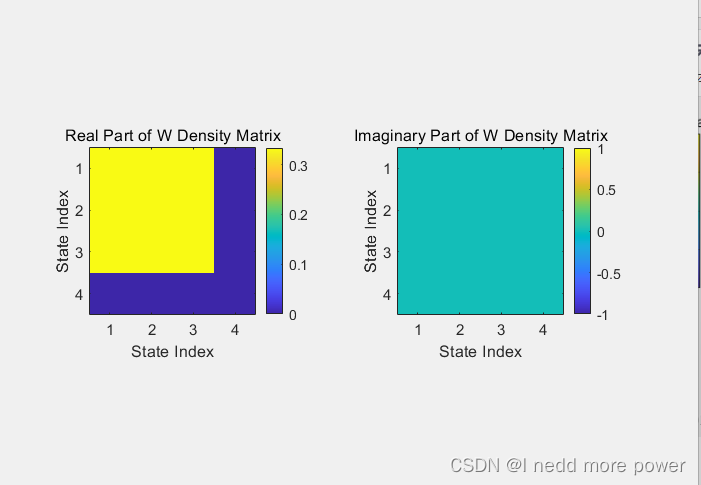
% 可视化W态
w_density_matrix = calculate_density_matrix(w_state);
visualize_density_matrix(w_density_matrix, 'W Density Matrix');
% 定义CNOT门和Hadamard门
CNOT = [1, 0, 0, 0;
0, 1, 0, 0;
0, 0, 0, 1;
0, 0, 1, 0];
H = 1/sqrt(2) * [1, 1;
1, -1];
Hadamard = kron(H, eye(2));
% 对GHZ态应用CNOT和Hadamard门
new_state = Hadamard * ghz_state;
new_state = CNOT * new_state;
% 可视化新的纠缠态密度矩阵
new_density_matrix = calculate_density_matrix(new_state);
visualize_density_matrix(new_density_matrix, 'New Entangled State Density Matrix');
效果