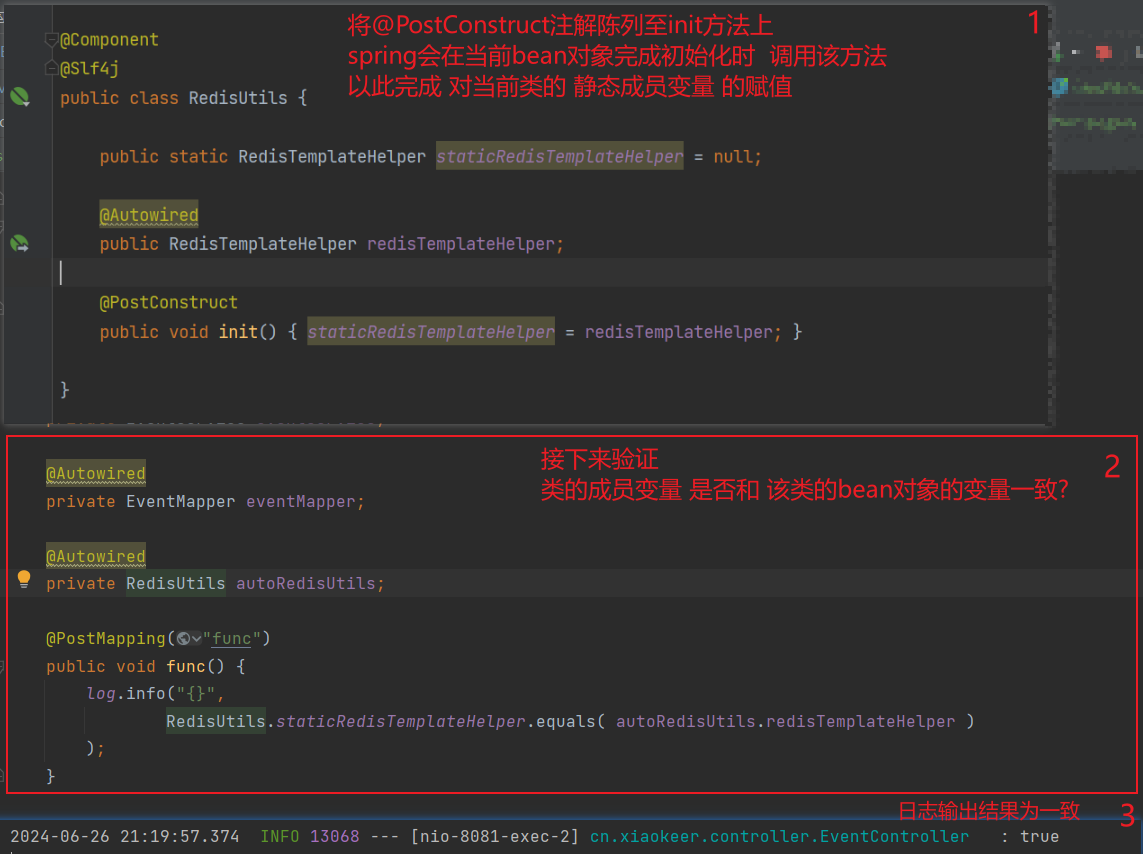
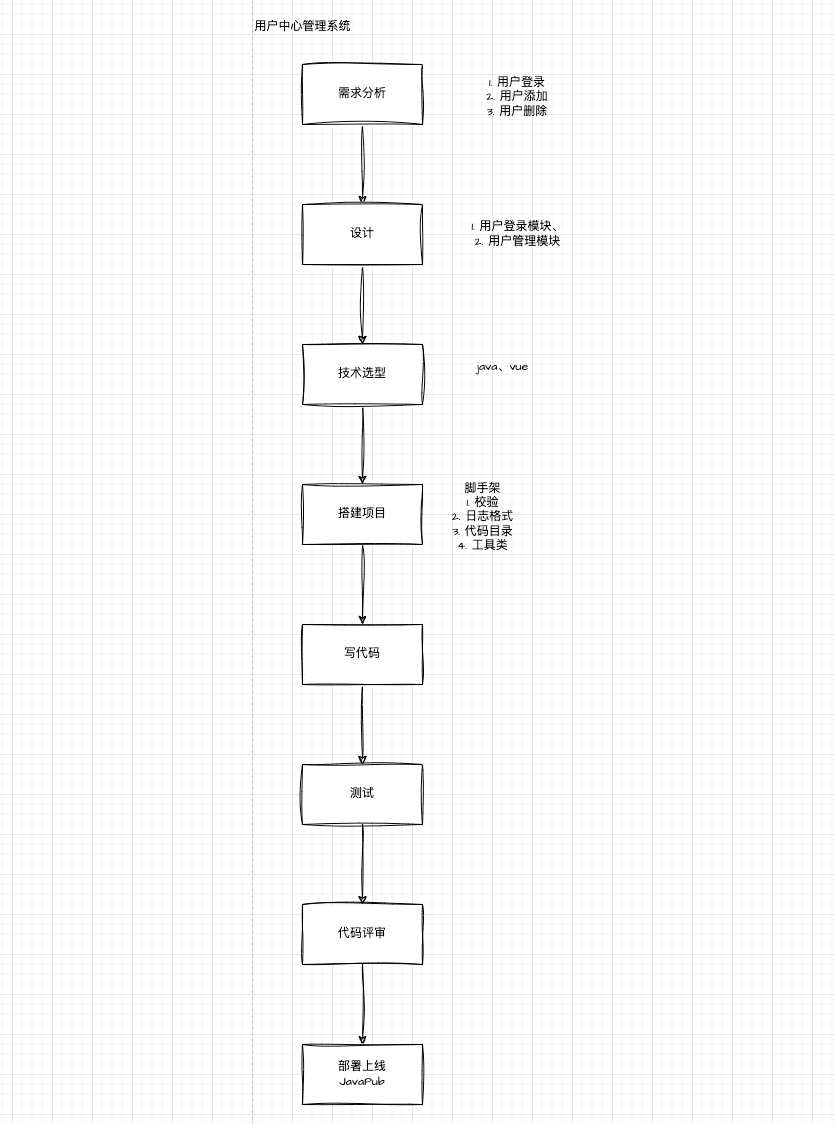
目录
线性代数基础概念:行列式
1. 行列式的定义
1.1 递归定义
1.2 代数余子式定义
1.3 几何定义
2. 行列式的性质
2.1 行列式等于其转置的行列式
2.2 交换两行或两列,行列式变号
2.3 将一行或一列乘以一个数 k,行列式乘以 k
2.4 将一行或一列加上另一行或列的倍数,行列式不变
2.5 行列式为 0 的充要条件是矩阵不可逆
2.6 行列式的乘法性质
3. 行列式的计算方法
3.1 展开式
3.2 初等变换
3.3 代数余子式
4. 行列式的应用
4.1 判断矩阵是否可逆
4.2 求解线性方程组
4.3 计算向量空间的体积
4.4 特征值与特征向量
5. 行列式总结
总结
线性代数基础概念:行列式
行列式是线性代数中一个重要的概念,它与矩阵密切相关,可以用来判断矩阵是否可逆、求解线性方程组、计算向量空间的体积等。
1. 行列式的定义
行列式 是一个将方阵映射到一个数的函数,它反映了矩阵的某些性质,例如矩阵的可逆性。
对于一个 n 阶方阵 A,它的行列式记为 det(A) 或 |A|。
行列式的定义可以通过以下几种方式给出:
1.1 递归定义
- 1 阶矩阵的行列式: 对于 1 阶矩阵 A = [a],它的行列式就是它唯一的元素,即 det(A) = a。
- n 阶矩阵的行列式: 对于 n 阶矩阵 A,它的行列式可以通过展开它的第一行或第一列来计算。
展开第一行:
det(A) = a11 * A11 - a12 * A12 + a13 * A13 - ... + (-1)^(n+1) * a1n * A1n
展开第一列:
det(A) = a11 * A11 - a21 * A21 + a31 * A31 - ... + (-1)^(n+1) * an1 * An1
其中,Aij 是矩阵 A 中第 i 行第 j 列元素的代数余子式,它等于矩阵 A 去掉第 i 行第 j 列后得到的 (n-1) 阶矩阵的行列式,并乘以 (-1)^(i+j)。
例如:
A = [ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
展开第一行计算行列式:
det(A) = 1 * | 5 6 | - 2 * | 4 6 | + 3 * | 4 5 |
= 1 * (5*9 - 6*8) - 2 * (4*9 - 6*7) + 3 * (4*8 - 5*7)
= 0
1.2 代数余子式定义
对于一个 n 阶矩阵 A,它的行列式可以表示为它的所有元素的代数余子式的线性组合。
det(A) = a11 * A11 + a12 * A12 + ... + a1n * A1n
其中,Aij 是矩阵 A 中第 i 行第 j 列元素的代数余子式。
例如:
A = [ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
根据代数余子式定义计算行列式:
det(A) = 1 * | 5 6 | - 2 * | 4 6 | + 3 * | 4 5 |
= 1 * (5*9 - 6*8) - 2 * (4*9 - 6*7) + 3 * (4*8 - 5*7)
= 0
1.3 几何定义
对于一个 n 阶矩阵 A,它的行列式可以表示为由矩阵 A 的列向量所张成的平行多面体的体积。
例如:
- 2 阶矩阵: 由矩阵 A 的两个列向量所张成的平行四边形的面积等于 det(A)。
- 3 阶矩阵: 由矩阵 A 的三个列向量所张成的平行六面体的体积等于 det(A)。
几何定义可以帮助我们理解行列式的几何意义,它反映了矩阵变换对空间的缩放比例。
2. 行列式的性质
行列式具有以下重要性质:
2.1 行列式等于其转置的行列式
det(A) = det(AT)
例如:
A = [ 1 2 ]
[ 3 4 ]
AT = [ 1 3 ]
[ 2 4 ]
det(A) = 1*4 - 2*3 = -2
det(AT) = 1*4 - 3*2 = -2
2.2 交换两行或两列,行列式变号
det(A) = -det(B)
其中 B 是由 A 交换两行或两列得到的矩阵。
例如:
A = [ 1 2 ]
[ 3 4 ]
B = [ 3 4 ]
[ 1 2 ]
det(A) = 1*4 - 2*3 = -2
det(B) = 3*2 - 4*1 = 2
2.3 将一行或一列乘以一个数 k,行列式乘以 k
det(kA) = k det(A)
例如:
A = [ 1 2 ]
[ 3 4 ]
2A = [ 2 4 ]
[ 6 8 ]
det(A) = 1*4 - 2*3 = -2
det(2A) = 2*8 - 4*6 = -4
2.4 将一行或一列加上另一行或列的倍数,行列式不变
det(A) = det(B)
其中 B 是由 A 将一行或一列加上另一行或列的倍数得到的矩阵。
例如:
A = [ 1 2 ]
[ 3 4 ]
B = [ 1 2 ]
[ 3+2*1 4+2*2 ] = [ 1 2 ]
[ 5 8 ]
det(A) = 1*4 - 2*3 = -2
det(B) = 1*8 - 2*5 = -2
2.5 行列式为 0 的充要条件是矩阵不可逆
det(A) = 0 当且仅当 A 不可逆
例如:
A = [ 1 2 ]
[ 2 4 ]
det(A) = 1*4 - 2*2 = 0
矩阵 A 不可逆,因为它的行列式为 0。
2.6 行列式的乘法性质
det(AB) = det(A) det(B)
例如:
A = [ 1 2 ]
[ 3 4 ]
B = [ 5 6 ]
[ 7 8 ]
det(A) = 1*4 - 2*3 = -2
det(B) = 5*8 - 6*7 = -2
det(AB) = det(A) det(B) = (-2) * (-2) = 4
3. 行列式的计算方法
3.1 展开式
通过展开行列式的第一行或第一列来计算行列式。
例如:
A = [ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
展开第一行计算行列式:
det(A) = 1 * | 5 6 | - 2 * | 4 6 | + 3 * | 4 5 |
= 1 * (5*9 - 6*8) - 2 * (4*9 - 6*7) + 3 * (4*8 - 5*7)
= 0
3.2 初等变换
通过对矩阵进行初等变换,将矩阵化为上三角矩阵或下三角矩阵,然后计算行列式。
例如:
A = [ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
对矩阵 A 进行初等变换,将矩阵化为上三角矩阵:
[ 1 2 3 ]
[ 0 -3 -6 ]
[ 0 0 0 ]
上三角矩阵的行列式等于对角线元素的乘积,因此 det(A) = 1 * (-3) * 0 = 0。
3.3 代数余子式
通过计算矩阵的代数余子式来计算行列式。
例如:
A = [ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
根据代数余子式定义计算行列式:
det(A) = 1 * | 5 6 | - 2 * | 4 6 | + 3 * | 4 5 |
= 1 * (5*9 - 6*8) - 2 * (4*9 - 6*7) + 3 * (4*8 - 5*7)
= 0
4. 行列式的应用
4.1 判断矩阵是否可逆
det(A) = 0 当且仅当 A 不可逆。
例如:
A = [ 1 2 ]
[ 2 4 ]
det(A) = 1*4 - 2*2 = 0
矩阵 A 不可逆,因为它的行列式为 0。
4.2 求解线性方程组
克莱姆法则可以用行列式来求解线性方程组。
例如:
x + 2y = 5
2x + 4y = 10
将方程组写成矩阵形式:
[ 1 2 ] [ x ] = [ 5 ]
[ 2 4 ] [ y ] [ 10 ]
根据克莱姆法则,方程组的解为:
x = det(Ax) / det(A)
y = det(Ay) / det(A)
其中,Ax 是将方程组的系数矩阵 A 的第一列替换为常数向量 [5, 10] 得到的矩阵,Ay 是将方程组的系数矩阵 A 的第二列替换为常数向量 [5, 10] 得到的矩阵。
Ax = [ 5 2 ]
[ 10 4 ]
Ay = [ 1 5 ]
[ 2 10 ]
det(A) = 1*4 - 2*2 = 0
det(Ax) = 5*4 - 2*10 = 0
det(Ay) = 1*10 - 5*2 = 0
由于 det(A) = 0,因此方程组无解。
4.3 计算向量空间的体积
由矩阵 A 的列向量所张成的平行多面体的体积等于 det(A)。
例如:
A = [ 1 2 ]
[ 3 4 ]
由矩阵 A 的两个列向量所张成的平行四边形的面积等于 det(A) = 14 - 23 = -2。
4.4 特征值与特征向量
行列式可以用来计算矩阵的特征值。
特征值 是一个数,它满足以下方程:
Ax = λx
其中 A 是一个矩阵,x 是一个非零向量,λ 是一个数。
特征向量 是一个非零向量 x,它满足上述方程。
为了求解矩阵 A 的特征值,我们可以将上述方程改写为:
(A - λI)x = 0
其中 I 是单位矩阵。
为了使方程有非零解,矩阵 (A - λI) 的行列式必须为 0:
det(A - λI) = 0
这个方程被称为特征方程,它的解就是矩阵 A 的特征值。
例如:
A = [ 2 1 ]
[ 1 2 ]
求解矩阵 A 的特征值:
det(A - λI) = det([ 2-λ 1 ]
[ 1 2-λ ]) = (2-λ)^2 - 1 = 0
解得 λ1 = 1,λ2 = 3。
求解矩阵 A 的特征向量:
- 对于 λ1 = 1:
(A - λ1I)x = 0
[ 1 1 ] [ x1 ] = [ 0 ]
[ 1 1 ] [ x2 ] [ 0 ]
解得 x1 = -x2,因此特征向量为 [1, -1] 的倍数。
- 对于 λ2 = 3:
(A - λ2I)x = 0
[ -1 1 ] [ x1 ] = [ 0 ]
[ 1 -1 ] [ x2 ] [ 0 ]
解得 x1 = x2,因此特征向量为 [1, 1] 的倍数。
5. 行列式总结
| 概念 | 描述 |
|---|---|
| 行列式 | 将方阵映射到一个数的函数 |
| 行列式的定义 | 递归定义、代数余子式定义、几何定义 |
| 行列式的性质 | 行列式等于其转置的行列式、交换两行或两列,行列式变号、将一行或一列乘以一个数 k,行列式乘以 k、将一行或一列加上另一行或列的倍数,行列式不变、行列式为 0 的充要条件是矩阵不可逆、行列式的乘法性质 |
| 行列式的计算方法 | 展开式、初等变换、代数余子式 |
| 行列式的应用 | 判断矩阵是否可逆、求解线性方程组、计算向量空间的体积、特征值与特征向量 |
总结
行列式是线性代数中的重要概念,它与矩阵密切相关,可以用来判断矩阵是否可逆、求解线性方程组、计算向量空间的体积等。理解行列式的定义、性质、计算方法和应用,是学习线性代数的关键。