1.引言
1.1.本文的主要内容
理解动态系统中的潜在因果因素,对于智能代理在复杂环境中进行有效推理至关重要。本文将深入介绍CITRIS,这是一种基于变分自编码器(VAE)的框架,它能够从时间序列图像中提取并学习因果表示,即便这些图像中的潜在因素已经遭受了外部干预。CITRIS通过利用时间序列中的一致性以及干预行为(以橙色表示),有效地从图像序列中识别和区分出因果变量(以蓝色表示)。与传统的因果表示学习方法不同,CITRIS将因果变量视为可能具有多个维度的向量,而非单一的标量值。此外,CITRIS通过整合归一化流技术,能够灵活地扩展其应用,以利用并解耦由预训练自动编码器捕获的表示。这一创新方法不仅提高了因果表示的准确性,还为未来在模拟到现实世界场景中应用因果表示学习开辟了新的可能性。
在接下来的内容中,我们将首先概述迅速发展的因果表示学习(CRL)领域。随后,我们会深入探讨CITRIS的工作原理,包括它是如何从时间序列图像中识别和学习因果变量的。最后,我们将通过一系列精心设计的实验来验证CITRIS的性能和优势。
1.2.CITRIS模型简介
CITRIS模型是一个变分自编码器框架,旨在从时间图像序列中学习因果表示,其中潜在的因果因素可能已经受到了干预。
1.2.1.背景和动机
-
在复杂多变的环境中,智能代理需要对周围世界的动态系统进行深入理解,以便做出准确的推理和决策。这要求代理能够识别并理解影响系统行为的潜在因果因素。例如,在自动驾驶车辆中,理解交通信号、行人和其他车辆之间的因果关系对于安全导航至关重要。
-
为了实现这一目标,CITRIS模型应运而生。CITRIS是一种先进的变分自编码器框架,专门设计用于从时间图像序列中提取和学习因果表示。这些图像序列可能已经包含了由于外部干预而发生变化的潜在因素。CITRIS通过分析图像随时间的变化以及观察到的干预,能够识别出影响系统状态的关键变量。
-
CITRIS模型的核心优势在于其对因果变量的多维表示能力。与传统的标量因果变量不同,CITRIS能够处理更为复杂的多维因果因素,如3D空间中的旋转角度。这种能力使得CITRIS在处理高维数据时更为灵活和强大。
-
此外,CITRIS通过引入归一化流,进一步扩展了其应用范围。归一化流允许CITRIS利用和解耦由预训练自动编码器获得的表示,这不仅提高了模型的泛化能力,也为将模型应用于未见过的因果因素实例提供了可能。这一点在模拟到现实世界的场景中尤为重要,因为它允许模型在现实世界中更好地应用和适应。
-
CITRIS的提出,不仅推动了因果表示学习领域的发展,也为智能代理在复杂环境中的决策和推理提供了新的工具和方法。随着技术的不断进步和应用的不断深入,CITRIS有望在未来的人工智能应用中发挥更大的作用。
1.2.2. 主要特点
-
多维因果变量的识别:CITRIS的一个显著创新是其对因果变量的多维处理能力。在传统的因果表示学习中,因果因素通常被视为单一的标量值,这限制了模型处理复杂系统的能力。CITRIS通过将因果变量视为多维向量,能够更准确地捕捉和表示现实世界中的复杂因果关系。例如,在三维空间中分析物体的旋转和平移时,CITRIS能够同时考虑多个角度和位置维度。
-
时间一致性与干预信息的融合:CITRIS框架利用时间序列数据中的一致性模式和已知的干预点(如图中的橙色标记),来识别和分离出影响图像序列的因果变量(如图中的蓝色标记)。这种方法不仅提高了因果推断的准确性,也使得模型能够更好地理解和预测系统在不同干预下的行为变化。
-
归一化流的创新应用:CITRIS通过引入归一化流,实现了对预训练自动编码器表示的有效利用和解耦。归一化流提供了一种灵活的方法来转换和映射复杂的、纠缠的潜在表示,使其成为易于处理和分析的因果表示。这种能力极大地扩展了CITRIS的应用范围,使其不仅能够处理原始数据,还能够整合和改进现有的机器学习模型。
-
泛化能力的增强:通过使用预训练的自动编码器,CITRIS能够学习到更为丰富和一般的特征表示。这种预训练策略不仅提高了模型对新数据的适应能力,还为模型提供了一种从模拟环境到现实世界场景的泛化桥梁。这对于机器人学习、自动驾驶车辆和其他需要高度适应性和泛化能力的领域尤为重要。
-
实验验证的高效性能:CITRIS在多个数据集上的实验表明,它在恢复因果变量方面优于现有方法。无论是在处理3D渲染图像序列,还是在处理具有复杂动态的游戏环境数据时,CITRIS都能够展示出其在因果表示学习方面的卓越性能。
-
未来研究方向的指引:CITRIS的提出为因果表示学习领域提供了新的研究方向,包括但不限于模拟到现实的泛化、多模态数据的因果理解、以及在更广泛的应用场景中部署和优化CITRIS模型。这些研究方向有望进一步推动人工智能在理解因果关系方面的进展。
1.2.3. 工作原理
-
变分自编码器框架:CITRIS基于变分自编码器(VAE)的原理构建,这是一种强大的生成模型,能够学习数据的潜在表示。通过VAE框架,CITRIS可以对图像序列进行编码和解码,同时提取出有用的因果信息。
-
时间一致性与因果识别:CITRIS通过分析图像序列中的时间一致性模式,识别出系统状态随时间变化的连贯性。结合已知的干预信息,CITRIS能够区分和识别出影响系统动态的关键因果变量,即使在存在外部干预的情况下也能保持识别的准确性。
-
多维因果变量的处理:CITRIS不将因果变量视为单一的标量,而是作为多维向量进行处理。这种处理方式使得CITRIS能够捕捉更复杂的因果关系,例如在三维空间中物体的旋转和平移,这些通常涉及多个维度的相互作用。
-
归一化流的集成:CITRIS通过引入归一化流,增强了模型对复杂因果结构的处理能力。归一化流是一种可逆的神经网络层,它允许模型对潜在表示进行复杂的变换,同时保持数据的完整性。这使得CITRIS能够从预训练的自动编码器中学习,并在此基础上进一步优化和解耦表示,以更好地捕捉因果关系。
-
优化与扩展能力:归一化流的应用不仅提升了CITRIS对复杂数据的处理能力,还为模型的扩展提供了灵活性。CITRIS可以通过归一化流轻松地整合新的数据和先验知识,从而在不同的应用场景中实现更好的泛化和适应性。
综合来看,可以看出CITRIS模型是一个功能强大的因果表示学习框架,它结合了时间一致性和干预信息来识别图像序列中的因果变量,并通过引入归一化流来优化其性能。CITRIS的提出为理解动态系统的潜在因果因素提供了新的视角和方法,具有重要的理论意义和应用价值。
1.3.因果表示学习(CRL)
因果表示学习(CRL)是一个新兴的机器学习领域,旨在通过学习和利用因果模型语义赋予的潜变量形式的表示,来结合机器学习和因果关系的核心优势。因果表示学习(CRL)是在因果推断理论基础之上构建起来的新交叉学科,主要探讨如何通过机器学习来建立一种有效的因果表示,并促进机器学习的发展。它旨在从因果推断的角度出发,探究一个或多个变量之间的因果关系,从而获得有效的因果信息。
1.3.1.关键方面
- 因果图模型:根据变量间的因果关系,通过关系网络的形式确立变量间的因果关系,并发掘出变量间的关键决定因素,为因果推断提供重要参考数据。
- 因果表示学习技术:利用机器学习技术构建因果图模型,从该模型中推断每个变量对因果关系的影响程度,并对数据集中某些变量之间的因果关系进行统计建模。
- 因果效应估计:评估因果模型中一个变量对另一个变量的影响程度,这通常涉及到对因果关系的量化分析。
- 因果建模方法:建立能够描述变量间因果关系的数学模型,这些模型通常用于预测、解释和干预系统行为。
近年来,因果表示学习(CRL)成为机器学习领域的研究热点,并受到越来越多的关注。一些重要的概念已经提出,用于因果表示学习的新算法也已经发展出来,如深度因果表征网络(DCNN)和深度因果回归模型(DCRM)。这些算法在提取和利用因果信息方面表现出强大的能力,为解决许多技术挑战提供了有效手段。
1.3.2.应用领域
因果表示学习在自然语言处理、机器学习和计算机视觉等领域有可能发挥重要作用。例如,在自然语言处理中,因果表示学习可以帮助理解文本中的因果关系,从而提高文本分析和生成的质量。在机器学习中,因果表示学习可以用于构建更鲁棒和可解释的模型,从而提高模型的泛化能力和可信度。在计算机视觉中,因果表示学习可以帮助识别图像中的关键特征,并理解这些特征之间的因果关系,从而提高图像识别和理解的准确性。
2.CITRIS模型理论
2.1.因果表示学习
近几十年来,机器学习作为人工智能领域的一个重要分支,其相较于早期的AI方法,显著的优势在于能够自动地从高维数据中提取有用特征。尽管如此,机器学习主要依赖于数据中的统计特性,而非数据生成背后的因果机制,这导致其在面对跨领域泛化和策略规划等任务时常常力不从心。
与此相对,因果推断不局限于数据的统计描述,而是进一步探究在数据背后的系统模型中,进行外部干预的效果。这种因果推理的能力要求我们预先知道影响数据的因果变量及其相互关系。然而,在现实世界中,许多观测数据,如图像中的对象,最初并未以这种变量的形式呈现。
因此,因果表示学习(Causal Representation Learning, CRL)作为一个新兴的研究领域,旨在从图像、视频等低层次数据中识别和构建这些因果变量及其相互关系。核心思想是,低层次的观测数据 X X X可以视为对因果系统 C 1 , … , C n C_1, \ldots, C_n C1,…,Cn 状态的一个视图:
X = h ( C 1 , … , C n ) , X = h(C_1, \ldots, C_n), X=h(C1,…,Cn),
其中
h
:
C
→
X
h: \mathcal{C} \rightarrow \mathcal{X}
h:C→X表示从因果系统状态空间到观测空间的非线性映射。在CRL中,研究者致力于估计函数
h
h
h的逆过程,例如使用神经网络将低层次的观测数据映射到对某些特定任务有用的高层次因果变量上。

2.1.1时间干预序列(TRIS)
CITRIS致力于在时间介入序列(TRIS)这一情境下识别因果变量。在TRIS框架中,我们假定存在一个由K个因果因素构成的潜在因果过程,这些因素以动态贝叶斯网络(DBN)的形式存在,表示为 ( C 1 , C 2 , . . . , C K ) (C_1, C_2, ..., C_K) (C1,C2,...,CK)。在这个因果图 G = ( V , E ) G = (V, E) G=(V,E)中,每个节点i对应一个因果因素 C i C_i Ci,可以是标量或向量,而每条边 ( i , j ) (i, j) (i,j)代表从 C i C_i Ci到 C j C_j Cj的因果关系。
在TRIS中,每个因果因素 C i C_i Ci在每个时间步t都有一个实例 C i t C_i^t Cit,它的因果父节点仅能是前一时间步t-1的因果因素。这意味着我们考虑的DBN是一个随时间变化的K因素过程 ( C 1 t , C 2 t , . . . , C K t ) t = 1 T (C_1^t, C_2^t, ..., C_K^t)_{t=1}^T (C1t,C2t,...,CKt)t=1T,这些因素根据DBN的时序动态而演变。此外,TRIS假设在每个时间步,一些因果因素可能已经被介入,我们可以知道介入的目标(尽管不知道具体的介入值)。介入目标用二进制向量 I t ∈ { 0 , 1 } K I^t \in \{0, 1\}^K It∈{0,1}K表示,其中第i个分量如果是1,则表示因果因素 C i C_i Ci在时间t被介入了。
在TRIS中,我们实际上并不直接观察到因果因素
(
C
t
)
t
=
1
T
(C^t)_{t=1}^T
(Ct)t=1T,而是只能获得伴随相应介入目标
(
I
t
)
t
=
2
T
(I^t)_{t=2}^T
(It)t=2T的高维观察序列
(
X
t
)
t
=
1
T
(X^t)_{t=1}^T
(Xt)t=1T。每个观察都是所有因果因素的噪声和混合视图。形式上,
X
t
=
h
(
C
1
t
,
C
2
t
,
.
.
.
,
C
K
t
,
E
o
t
)
X^t = h(C_1^t, C_2^t, ..., C_K^t, E_o^t)
Xt=h(C1t,C2t,...,CKt,Eot),其中
E
o
t
E_o^t
Eot代表噪声,而
h
:
C
×
E
→
X
h: \mathcal{C} \times \mathcal{E} \rightarrow \mathcal{X}
h:C×E→X是从因果因素空间
C
\mathcal{C}
C和噪声变量空间
E
\mathcal{E}
E映射到观察空间
X
\mathcal{X}
X的函数。

TRIS的设置非常通用,能够涵盖许多动态系统。实际上,CITRIS(以及iCITRIS,我们在这篇文档中没有讨论)已经成功地在从3D渲染对象到弹球和乒乓球等不同设置中识别出了因果结构。



在本文的后续部分,我们将专注于Causal3DIdent数据集,并在下一部分中提供更详细的描述。
2.1.2加载数据集
接下来,我们将探索Causal3DIdent数据集。该数据集包含了一系列图像,并且每个时间点都配有相应的干预目标。在下方的代码单元中,我们将载入数据集的一个小型样本进行查看。
# 导入需要的库
import numpy as np
import os
# 假设 'CITRIS_DL2' 是包含 'data' 文件夹的目录,而 'causal3d.npz' 是 'data' 文件夹中的一个文件
# 使用 np.load 函数加载 'causal3d.npz' 文件,并将结果存储在一个名为 causal3d_dataset 的字典中
causal3d_dataset = dict(np.load(os.path.join('CITRIS_DL2', 'data', 'causal3d.npz')))
# 打印出 causal3d_dataset 字典中所有的键(即NumPy数组的名称)
print(causal3d_dataset.keys())
# 中文注释:
# 这段代码的目的是从 'CITRIS_DL2' 目录下的 'data' 文件夹中加载一个名为 'causal3d.npz' 的NumPy压缩文件。
# np.load 函数会返回一个类似字典的对象,其中包含了文件中存储的所有NumPy数组。
# 使用 dict() 函数将这个类似字典的对象转换为真正的字典,方便后续处理。
# 最后,使用 print 函数打印出这个字典中所有的键,即存储在 'causal3d.npz' 文件中的所有NumPy数组的名称。
干预目标指出了哪些因果变量受到了干预。在Causal3DIdent数据集中,我们关注以下7个因果变量,它们总共包含了11个因果维度:
| 变量 | 取值范围 |
|---|---|
| 对象位置 (pos_o) | [ x , y , z ] ∈ [ − 2 , 2 ] 3 [x, y, z] \in [-2, 2]^3 [x,y,z]∈[−2,2]3 |
| 对象旋转 (rot_o) | [ α , β ] ∈ [ 0 , 2 π ) 2 [\alpha, \beta] \in [0, 2\pi)^2 [α,β]∈[0,2π)2 |
| 聚光灯旋转 (rot_s) | θ ∈ [ 0 , 2 π ) \theta \in [0, 2\pi) θ∈[0,2π) |
| 对象色调 (hue_o) | h obj ∈ [ 0 , 2 π ) h_\text{obj} \in [0, 2\pi) hobj∈[0,2π) |
| 聚光灯色调 (hue_s) | h light ∈ [ 0 , 2 π ) h_\text{light} \in [0, 2\pi) hlight∈[0,2π) |
| 背景色调 (hue_b) | h bg ∈ [ 0 , 2 π ) h_\text{bg} \in [0, 2\pi) hbg∈[0,2π) |
| 对象形状 (obj_s) | s ∈ { 茶壶, 奶牛, 头部, 马, 犰狳, 龙, 野兔 } s \in \{\text{茶壶, 奶牛, 头部, 马, 犰狳, 龙, 野兔}\} s∈{茶壶, 奶牛, 头部, 马, 犰狳, 龙, 野兔} |
请注意,在我们的实验中,我们将使用Causal3DIdent的一个变体,其中只包含茶壶作为可能的对象形状。这些因果变量之间的关系在以下图表中展示。
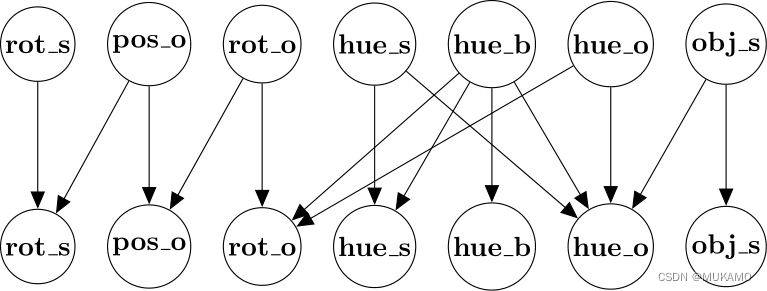
以下是每个时间步被介入的因果变量。第
i
i
i个介入目标意味着第
(
i
−
1
)
(i-1)
(i−1)张图像的因果变量被介入,从而产生了第
i
i
i张图像。
`time_steps = 4`
`print(causal3d_dataset['interventions'][0:time_steps])`
请注意,每个介入目标具有12个维度,而不是11个。这是因为最后一个维度是对象材质,CITRIS并未对其进行建模。在下一个单元中,我们将绘制一系列图像。请注意,上面打印的介入目标是如何影响对象和周围环境的。
`plt.rcParams['figure.figsize'] = [10, 5]`
`for i in range(time_steps):`
`plt.subplot(1, time_steps, i+1)`
`plt.imshow(causal3d_dataset['images'][i])`
`plt.xlabel(f't = {i}')`
`plt.xticks([])`
`plt.yticks()`
`plt.show()`

2.2.CITRIS理论
2.2.1.最小因果变量
在TRIS框架内,如果两个因果因素总是一并被介入,或者根本没有被介入,我们通常难以将它们区分开来。此外,多维因果变量在TRIS中可能无法完全被识别,因为介入可能只影响了其中的一部分维度。在这种情况下,我们可能只能识别所谓的“最小因果变量”,它仅涵盖了那些严格受到介入影响的因果信息。例如,考虑以下因果过程:一个球在当前盒子内可以自由移动,但只有在介入的作用下才能跳到另一个盒子中(这种介入保持了球在盒子内的相对位置不变)。
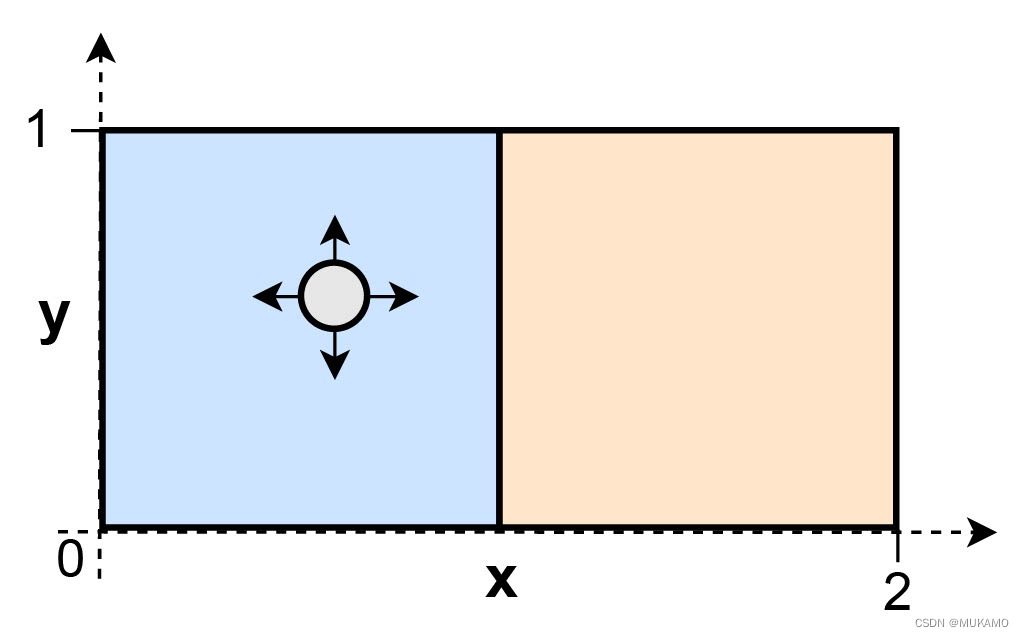
如果我们用两个因果变量来模拟这个过程,即盒子内的相对位置
x
′
x'
x′(我们从不直接介入)和当前所在的盒子
b
b
b,我们只能识别出因果变量
b
b
b,因为
x
′
x'
x′ 不受介入的影响。换句话说,在本例中,( b$ 就是最小因果变量。
为了正式定义最小因果变量,设想一个可逆映射 s i : D i M i → D i var × D i inv s_i: \mathcal{D}_i^{M_i} \rightarrow \mathcal{D}_i^\text{var} \times \mathcal{D}_i^\text{inv} si:DiMi→Divar×Diinv,它将每个因果变量 C i t C_i^t Cit 分解为与介入有关的依赖部分 s i var ( C i t ) s^\text{var}_i(C^{t}_i) sivar(Cit) 和与介入无关的部分 s i inv ( C i t ) s^\text{inv}_i(C^{t}_i) siinv(Cit)(注意,这个可逆映射并不唯一)。我们的目标是识别出这样的一种分解,其中 s i var ( C i t ) s^\text{var}_i(C^{t}_i) sivar(Cit) 只包含那些真正依赖于介入的信息。根据这种分解,( s\text{var}_i(C{t}_i)$ 被定义为最小因果变量,并用 s i var ∗ ( C i t ) s^{\text{var}^*}_i(C^{t}_i) sivar∗(Cit) 来表示。
2.2.2.最小因果变量学习
为了学习TRIS中的最小因果变量,CITRIS使用数据三元组 { x t , x t + 1 , I t + 1 } \{x^t, x^{t+1}, I^{t+1}\} {xt,xt+1,It+1}来学习两个组件,以近似观测函数的逆。
- 一个从观测空间到潜在空间的可逆映射: g θ : X → Z g_\theta: \mathcal{X} \to \mathcal{Z} gθ:X→Z。
- 一个分配函数 ψ : [ [ 1.. M ] ] → [ [ 0.. K ] ] \psi: [\![1..M]\!]\to[\![0..K]\!] ψ:[[1..M]]→[[0..K]],该函数将潜在空间的每个维度映射到因果因子集合 C \mathcal{C} C中的一个(或零,表示非因果维度)。
对于分配函数 ψ \psi ψ,如果 ψ ( j ) = 0 \psi(j) = 0 ψ(j)=0(其中 j ∈ [ [ 1.. M ] ] j \in [\![1..M]\!] j∈[[1..M]]),这表示潜在维度 z j z_j zj并不对应于任何最小因果变量的维度,而是与某种非因果因素(可能是 s i inv ( C i t ) s^\text{inv}_i(C^{t}_i) siinv(Cit)的某个维度)相关。此外,我们定义 z ψ i = { z j ∣ j ∈ [ [ 1.. M ] ] , ψ ( j ) = i } z_{\psi_i} = \{z_j \mid j \in [\![1..M]\!], \psi(j) = i\} zψi={zj∣j∈[[1..M]],ψ(j)=i}为 ψ \psi ψ分配给因果变量 C i C_i Ci的所有潜在变量的集合。
为了促进因果因子的解耦,CITRIS在潜在空间中建模了一个转换先验,确保每个潜在变量仅与一个干预目标相关联。
在CITRIS模型中,转换先验被分解为基于干预目标的条件概率的乘积形式:
p ϕ ( z t + 1 ∣ z t , I t + 1 ) = ∏ i = 0 K p ϕ ( z ψ i t + 1 ∣ z t , I i t + 1 ) , p_{\phi}\left(z^{t+1}|z^{t}, I^{t+1}\right) = \\\prod_{i=0}^{K}p_{\phi}\left(z_{\psi_i}^{t+1}|z^{t}, I_{i}^{t+1}\right), pϕ(zt+1∣zt,It+1)=i=0∏Kpϕ(zψit+1∣zt,Iit+1),
其中, I 0 t + 1 I_0^{t+1} I0t+1 被视为没有干预的状态(通常设为0或空值)。结合转换先验和可逆映射 g θ g_\theta gθ,CITRIS的目标是最大化以下似然函数:
p ϕ , θ ( x t + 1 ∣ x t , I t + 1 ) = ∣ ∂ g θ ( x t + 1 ) ∂ x t + 1 ∣ ⋅ p ϕ ( z t + 1 ∣ z t , I t + 1 ) p_{\phi,\theta}(x^{t+1}|x^{t},I^{t+1}) =\\ \left|\frac{\partial g_{\theta}(x^{t+1})}{\partial x^{t+1}}\right| \cdot p_{\phi}(z^{t+1}|z^{t}, I^{t+1}) pϕ,θ(xt+1∣xt,It+1)= ∂xt+1∂gθ(xt+1) ⋅pϕ(zt+1∣zt,It+1)
若模型 M \mathcal{M} M在最大化似然函数 L ϕ , θ ( x t + 1 ∣ x t , I t + 1 ) \mathcal{L}_{\phi,\theta}(x^{t+1}|x^{t},I^{t+1}) Lϕ,θ(xt+1∣xt,It+1)的同时,也最大化了 z ψ 0 z_{\psi_0} zψ0的信息量,且满足干预变量之间不存在确定性依赖关系,则 M \mathcal{M} M被证明能够识别任何因果系统 S \mathcal{S} S。这意味着,通过 M \mathcal{M} M,我们可以识别出系统 S \mathcal{S} S中的最小因果变量,直至一个可逆变换的程度。直观上,潜在变量 z ψ i z_{\psi_i} zψi仅捕捉了严格依赖于对应干预目标 I i t + 1 I_i^{t+1} Iit+1的因果因子 C i C_i Ci的信息。
我们已经构建了一个理论框架,旨在从具有已知干预目标的图像序列中识别出因果变量。接下来,我们将介绍该模型 M \mathcal{M} M的两种实际实现变体:CITRIS-VAE和CITRIS-NF。
2.2.3.CITRIS-VAE
在CITRIS模型中,为了识别图像序列中的因果变量,我们采用了两个关键组件的近似方法:可逆映射 g θ : X → Z g_\theta: \mathcal{X} \to \mathcal{Z} gθ:X→Z和分配函数 ψ : [ 1.. M ] → [ 0.. K ] \psi: [1..M] \to [0..K] ψ:[1..M]→[0..K]。为了具体实现这一框架,我们引入了CITRIS-VAE,它利用变分自编码器(VAE)来近似 g θ g_\theta gθ。
CITRIS-VAE通过编码器 q θ q_\theta qθ和解码器 p θ p_\theta pθ来优化以下证据下界(ELBO):
L ELBO = − E z t + 1 [ log p θ ( x t + 1 ∣ z t + 1 ) ] + E z t , ψ [ ∑ i = 0 K D KL ( q θ ( z ψ i t + 1 ∣ x t + 1 ) ∣ ∣ p ϕ ( z ψ i t + 1 ∣ z t , I i t + 1 ) ) ] \mathcal{L}_{\text{ELBO}} = -\mathbb{E}_{z^{t+1}}\left[\log p_{\theta}\left(x^{t+1}|z^{t+1}\right)\right] + \\\mathbb{E}_{z^{t},\psi}\left[\sum_{i=0}^{K} D_{\text{KL}}\left(q_{\theta}(z_{\psi_{i}}^{t+1}|x^{t+1})||p_{\phi}(z_{\psi_{i}}^{t+1}|z^{t}, I_{i}^{t+1})\right)\right] LELBO=−Ezt+1[logpθ(xt+1∣zt+1)]+Ezt,ψ[i=0∑KDKL(qθ(zψit+1∣xt+1)∣∣pϕ(zψit+1∣zt,Iit+1))]
在这个公式中,第一项表示解码器重建原始数据 x t + 1 x^{t+1} xt+1的准确度,而第二项则是确保分配给不同因果变量的潜变量块在给定前一时间步的潜变量 z t z^t zt和干预 I i t + 1 I_i^{t+1} Iit+1的条件下是独立的。这是通过KL散度( D KL D_{\text{KL}} DKL)实现的,它度量了编码器分布 q θ ( z ψ i t + 1 ∣ x t + 1 ) q_{\theta}(z_{\psi_{i}}^{t+1}|x^{t+1}) qθ(zψit+1∣xt+1)和转换先验 p ϕ ( z ψ i t + 1 ∣ z t , I i t + 1 ) p_{\phi}(z_{\psi_{i}}^{t+1}|z^{t}, I_{i}^{t+1}) pϕ(zψit+1∣zt,Iit+1)之间的差异。
为了确保潜变量分配的正确性,我们采用Gumbel-Softmax分布来学习分配函数
ψ
\psi
ψ。通过这种方式,CITRIS-VAE能够捕捉图像序列中的因果结构,并识别出与不同干预目标相关的因果变量。

CITRIS-VAE的整体架构通过结合VAE的灵活性和CITRIS的理论框架,为从图像序列中识别因果变量提供了一种实用的方法。
class CITRISVAE_MINIMAL(nn.Module):
"""
这是一个CITRIS-VAE的简化实现,用于教学目的。
为了清晰起见,省略了一些步骤和细节。
你可以在以下地址找到完整版本:
https://github.com/phlippe/CITRIS/blob/main/models/citris_vae/lightning_module.py
"""
def __init__(self, encoder, decoder, transition_prior):
super().__init__()
# 编码器和解码器
# Encoder-Decoder
self.encoder, self.decoder = encoder, decoder
# 转换先验
# Transition prior
self.prior_t1 = transition_prior
def forward(self, x):
"""
返回x的重构
"""
# 编码
# Encode
z_mean, z_logstd = self.encoder(x)
# 重参数化技巧
# Reparameterization trick
z_sample = z_mean + torch.randn_like(z_mean) * z_logstd.exp()
# 解码
# Decode
x_rec = self.decoder(z_sample)
return x_rec, z_sample, z_mean, z_logstd
def _get_loss(self, batch):
"""
返回一批数据的损失
"""
# 解包批次数据
# Unpack batch
imgs, labels, target = batch
# 编码
# Encode
z_mean, z_logstd = self.encoder(imgs)
# 重参数化技巧
# Reparameterization trick
z_sample = z_mean + torch.randn_like(z_mean) * z_logstd.exp()
# 解码
# Decode
x_rec = self.decoder(z_sample)
# 计算每对帧之间的KL散度
# Calculate KL divergence between every pair of frames
kld = self.prior_t1.kl_divergence(z_t=z_mean[:, :-1],
target=target,
z_t1_mean=z_mean[:, 1:],
z_t1_logstd=z_logstd[:, 1:],
z_t1_sample=z_sample[:, 1:])
# 重构损失
# Reconstruction loss
rec_loss = F.mse_loss(x_rec, labels[:, 1:], reduction='none').sum()
# 获取总损失
# Get the full loss
loss = (kld + rec_loss.sum(dim=1)).mean()
return loss
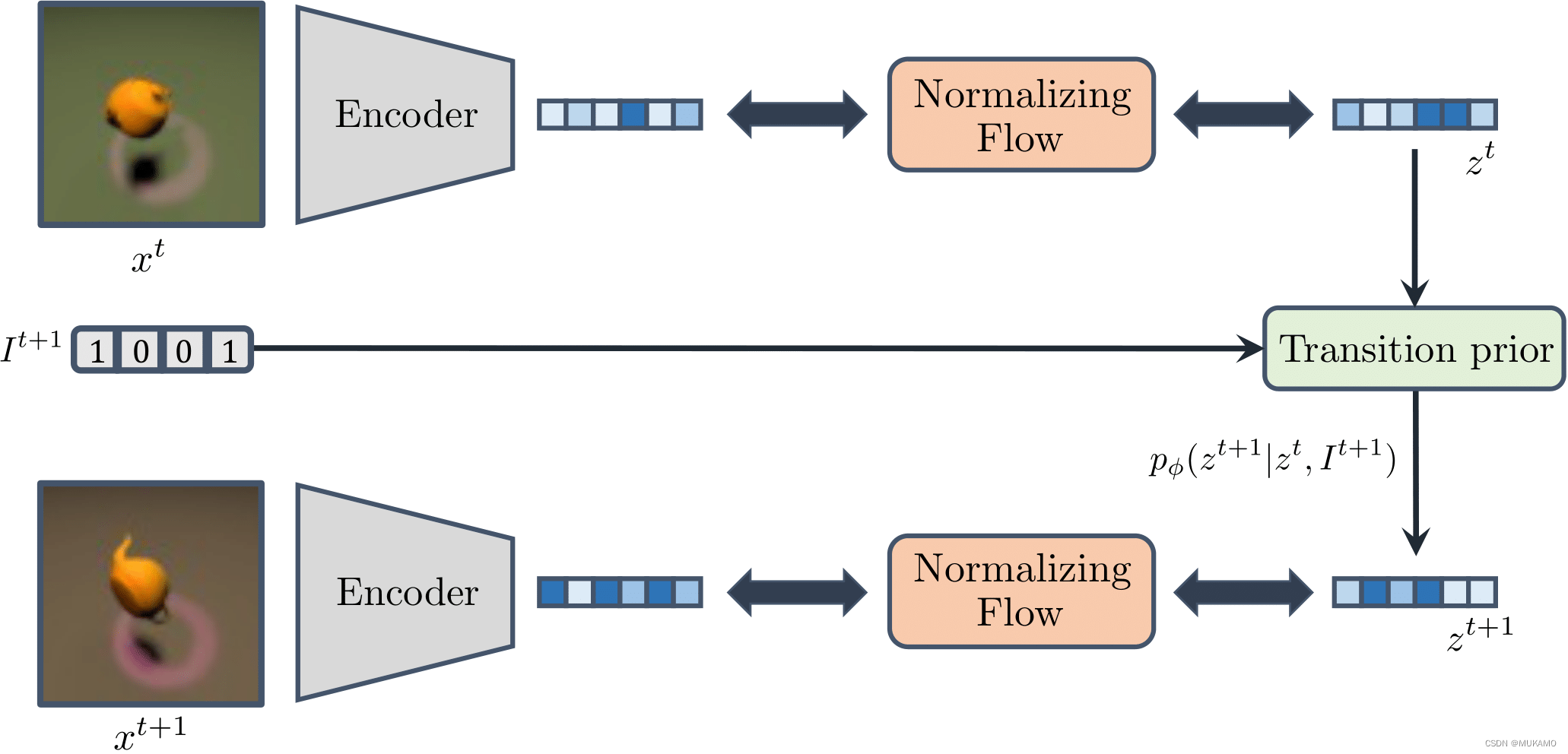
2.2.4.CITRIS-NF
VAE的一个明显局限在于,它在处理包含众多虽小却对因果系统建模至关重要的细节的复杂图像时可能会显得力不从心。为了克服这一挑战,CITRIS-NF将 g θ g_\theta gθ的学习过程分解为以下两个部分:
- 预训练自编码器(AE):首先,它学习如何编码高维观测数据,而无需在潜在空间中明确分离不同的维度。
- 归一化流(NF):接着,它进一步学习如何将自编码器产生的纠缠潜在表示转换为一个解纠缠的潜在表示。
与VAE相比,预训练自编码器不受限于潜在分布与转换先验的相似性要求,这使得它能够更加灵活地建模复杂的边际分布。下面,我们将对CITRIS-NF的架构进行可视化展示。
class CITRISNF_MINIMAL(nn.Module):
"""
这是CITRIS-NF的简化实现,用于教学目的。
为了清晰起见,省略了一些步骤和细节。
你可以在以下地址找到完整版本:
https://github.com/phlippe/CITRIS/blob/main/models/citris_nf/lightning_module.py
"""
def __init__(self, encoder, decoder, transition_prior, flow):
super().__init__()
# 编码器和解码器
# Encoder-Decoder
self.encoder, self.decoder = encoder, decoder
# 转换先验
# Transition prior
self.prior_t1 = transition_prior
# 归一化流(Normalizing Flow)
# Normalizing Flow
self.flow = flow
def forward(self, x, noise_level=0.0):
"""
返回x的重构
注意:在前向传播中我们不使用流。
流仅用于解纠缠潜在空间。
"""
# 编码
# Encode
z = self.encoder(x)
# 添加一些噪声
# Add some noise
z = z + torch.randn_like(z) * noise_level
# 解码器期望原始的潜在空间。
# 执行流并随后逆转没有效果。
# 因此,我们在这里跳过流。
# # 执行流以解纠缠潜在空间
# z, _ = self.flow(z)
# # 逆转流以获取原始的潜在空间
# z = self.flow.reverse(z)
# 解码
# Decode
x_rec = self.decoder(z)
# 返回重构的x和潜在变量z
return x_rec, z # 中文注释
def _get_loss(self, batch, noise_level=0.0):
"""
返回一批数据的损失
"""
# 解包批次数据
# Unpack batch
imgs, target = batch
# 编码图像
# Encode
z = self.encoder(imgs)
# 添加一些噪声
# Add some noise
z = z + torch.randn_like(z) * noise_level
# 执行流(Normalizing Flow)
# Execute the flow
z_sample, ldj = self.flow(z) # ldj = log(det(Jacobian)),即对数雅可比行列式
# 计算转换先验的负对数似然
# Calculate the negative log likelihood of the transition prior
# 注意:这里假设z_sample是一个时间步序列,我们使用了t时刻和t+1时刻的z来计算转换先验的NLL
nll = self.prior_t1.sample_based_nll(z_t=z_sample[:, :-1], # t时刻的z
z_t1=z_sample[:, 1:], # t+1时刻的z
target=target)
# 将LDJ(对数雅可比行列式)和先验NLL相加得到总损失
# Add LDJ and prior NLL for full loss
# 注意:通常我们会乘以一个负号来最小化损失,但这里假设flow的ldj已经是负的
loss = nll + ldj
return loss
2.2.5.目标分类
为了更有效地促进潜在空间中的解纠缠,CITRIS-VAE和CITRIS-NF都可以引入一个目标分类器。这个分类器被训练用来根据时间序列中的潜变量预测干预目标,具体来说,就是预测 p ( I t + 1 ∣ z t , z ψ i t + 1 ) p(I^{t+1}|z^{t}, z_{\psi_{i}}^{t+1}) p(It+1∣zt,zψit+1),其中 i i i的范围是 [ 0 , K ] [0, K] [0,K]。为了实现这一目标,我们训练 z ψ i t + 1 z_{\psi_{i}}^{t+1} zψit+1,使其与预期因果变量 C i C_i Ci的干预目标 I i t + 1 I_i^{t+1} Iit+1之间的互信息最大化。这样,潜变量 z ψ i t + 1 z_{\psi_{i}}^{t+1} zψit+1就能更好地捕捉到与特定干预目标相关的因果变量信息。
3.实验
为了更深入地了解CITRIS的能力,我们现在将进行一系列实验。首先,我们将研究CITRIS在Causal3DIdent数据集上分解因果因素的效果。随后,我们将展示如何利用CITRIS学习到的潜在维度在图像空间中进行干预,并逆向分析当我们在输入图像中改变某个因果变量时,这些潜在维度会如何变化。
为此,我们将使用在Causal3DIdent数据集上预训练的CITRIS-NF的一个变体来进行这些实验。
3.1.加载预训练模型
# 定义预训练的CITRIS模型的路径
pretrained_CITRIS_path = os.path.join(CHECKPOINT_PATH, "citris" + ".ckpt")
# 检查预训练模型文件是否存在,并加载模型
if os.path.isfile(pretrained_CITRIS_path):
print(f"在 {pretrained_CITRIS_path} 发现预训练模型,正在加载...")
model = CITRISNF.load_from_checkpoint(pretrained_CITRIS_path)
model.eval()
3.2.三元组评估
为了进行三元组评估以揭示潜在变量之间的复杂依赖关系,我们将遵循以下步骤:
-
数据采样:从原始测试数据集中随机选择两个图像样本,这两个图像样本将构成三元组的前两个元素,分别记作
Image A和Image B。 -
因果因素提取:对于
Image A和Image B,我们利用预训练的CITRIS模型或其他因果分析工具来提取其潜在的因果因素(如形状、颜色、纹理等)。这些因果因素反映了图像背后的关键生成要素。 -
因果因素组合:在提取出
Image A和Image B的因果因素之后,我们按照某种随机规则将它们进行组合,从而创建一个新的合成图像Image C。这个合成图像可能包含了来自Image A的某些因果因素,来自Image B的某些因果因素,或者是两者的混合。 -
潜在空间编码:将
Image A、Image B和合成图像Image C输入到CITRIS模型中,获得它们在潜在空间中的表示。这些表示反映了图像在模型学习到的因果结构中的位置。 -
三元组评估:在潜在空间中,我们分析
Image A、Image B和Image C的表示之间的关系。具体来说,我们可以计算这些表示之间的距离(如欧氏距离)或相似度(如余弦相似度),从而揭示出因果因素在潜在空间中的依赖和交互模式。 -
结果分析:根据评估结果,我们可以得出关于潜在变量之间复杂依赖关系的结论。例如,如果
Image C的潜在表示更接近Image A而不是Image B,那么这可能意味着某些因果因素在组合时具有更强的影响力或优先级。
通过这种三元组评估方法,我们能够更深入地理解CITRIS模型在捕捉和表示因果结构方面的能力,并为其在未来的研究和应用中提供有价值的指导。
# 首先检查单个图像三元组可能是什么样子
triplets = dict(np.load(os.path.join('CITRIS_DL2', 'data', 'causal3d_triplets.npz')))
image_triplet = triplets['images'][0]
# 设置图像显示的大小
plt.rcParams['figure.figsize'] = [10, 5]
labels = ['图像1', '图像2', '因果因素组合']
for i in range(3):
plt.subplot(1, 3, i+1)
plt.imshow(image_triplet[i])
plt.xlabel(labels[i])
plt.xticks([])
plt.yticks([])
# 显示图像
plt.show()

三元组数据集额外包含了一个二进制掩码
m
\mathbf{m}
m,该掩码是一个长度为
K
K
K 的向量,其中每个元素
m
k
m_k
mk 指示了对应的因果因素
C
k
C_k
Ck 的来源。具体而言,如果
m
k
m_k
mk 为
1
1
1,则表示
C
k
C_k
Ck 是从第二个图像中选取的;如果
m
k
m_k
mk 为
0
0
0,则表示
C
k
C_k
Ck 是从第一个图像中选取的。
triplet_mask = triplets['mask'][0]
mask_names = ['x位置', 'y位置', 'z位置', 'α旋转', 'β旋转', 'γ旋转', '聚光灯θ', '物体色调', '聚光灯色调', '背景色调', '形状', '材质']
assigned_to = {0: [], 1: []}
for mask_name, mask in zip(mask_names, triplet_mask):
assigned_to[mask].append(mask_name)
# 打印分配给图像1和图像2的因素
print(f"分配给图像1: {assigned_to[0]}")
print(f"分配给图像2: {assigned_to[1]}")
在评估过程中,我们首先对两个测试图像进行独立编码,然后模拟第三个图像在潜在空间中的因果因素组合过程。具体来说,我们根据从两个测试图像中提取的因果因素进行随机组合,并应用这些组合到潜在空间中的表示。接下来,我们使用解码器将经过组合的潜在表示解码为一个新的图像。
理想情况下,这个新生成的图像应该与通过组合两个原始图像的因果因素而实际创建的真实第三个图像非常相似。这种相似性可以通过计算两个图像之间的视觉相似度度量(如像素级别的差异、结构相似性指数等)来评估。通过这种方式,我们能够评估模型在模拟和生成具有特定因果因素组合的图像方面的性能。
# 定义一个无梯度的编码函数
@torch.no_grad()
def encode(imgs):
# 将图像数据转换为torch张量,并进行归一化处理
imgs = torch.from_numpy(imgs)[...,:3]
# 根据图像维度进行适当的排列和展平
if len(imgs.shape) == 5:
imgs = imgs.permute(0, 1, 4, 2, 3)
imgs = imgs.flatten(0, 1)
else:
imgs = imgs.permute(0, 3, 1, 2)
imgs = imgs.flatten(0)
print(imgs.shape)
imgs = imgs.float() / 255.0
imgs = imgs * 2.0 - 1.0
# 使用CITRIS模型的编码器对图像进行编码
encs = model.autoencoder.encoder(imgs)
encs = encs.unflatten(0, (-1, triplets['images'].shape[1]))
return encs
# 定义一个无梯度的三元组重建函数
@torch.no_grad()
def triplet_reconstruction(imgs, source):
# 编码图像
x_encs = encode(imgs)
# 通过归一化流传递以解耦潜在空间
input_samples, _ = model.flow(x_encs[:,:2].flatten(0, 1))
input_samples = input_samples.unflatten(0, (-1, 2))
# 获取潜在变量对因果变量的分配
target_assignment = model.prior_t1.get_target_assignment(hard=True)
# 根据掩码从图像1的编码中获取潜在变量
mask_1 = (target_assignment[None,:,:] * (1 - source[:,None,:])).sum(dim=-1)
# 从图像2中获取其余的
mask_2 = 1 - mask_1
# 从图像1和图像2的因果变量组合创建编码
triplet_samples = mask_1 * input_samples[:,0] + mask_2 * input_samples[:,1]
# 从triplet_samples反向流
triplet_samples = model.flow.reverse(triplet_samples)
# 解码并获取新图像
triplet_rec = model.autoencoder.decoder(triplet_samples)
return triplet_rec
# 调用三元组重建函数
triplet_rec = triplet_reconstruction(triplets['images'][0:3], triplets['mask'][0:3, [0,1,2,3,4,6,7,8,9,10]])
print(triplet_rec.shape) # 输出编码后图像的形状
为了定义一个函数来将图像数据规范化以便显示,我们可以编写一个函数,该函数将图像数据缩放到适合显示的范围。在图像处理的上下文中,常见的做法是将像素值缩放到0到1或-1到1的范围内,具体取决于图像数据类型(如8位无符号整数、浮点数等)。
def normalize(imgs):
imgs = imgs.numpy().transpose(1,2,0)
imgs = (imgs + 1)/2
imgs = imgs*255
return imgs.astype(int)
# 绘制原始三元组图像和重建的三元组图像
fig, axs = plt.subplots(3, 4, figsize=(8, 6))
for i in range(3):
axs[i, 0].imshow(triplets['images'][i][0])
axs[i, 0].set_xlabel('图像1')
axs[i, 1].imshow(triplets['images'][i][1])
axs[i, 1].set_xlabel('图像2')
axs[i, 2].imshow(triplets['images'][i][2])
axs[i, 2].set_xlabel('真实情况')
axs[i, 3].imshow(normalize(triplet_rec[i]))
axs[i, 3].set_xlabel('预测')
# 隐藏所有子图的坐标轴
for ax in axs.flat:
ax.set_xticks([])
ax.set_yticks([])
# 调整子图布局并显示
plt.tight_layout()
plt.show()

CITRIS通过仅依赖组合的潜在维度重构的三元组图像,与真实的组合图像高度相似,这充分展示了CITRIS学习到的潜在维度不仅准确地捕捉了图像空间的分布特征,而且实现了良好的解耦,即每个潜在维度专注于一个单独的因果变量,并不包含其他任何因果变量的信息。
3.3.实施干预
鉴于之前的结果,我们得知CITRIS能够从时间序列中学习到因果表示,并且这暗示我们有能力利用这些潜在维度来控制生成图像中每个因果变量的值。简而言之,这意味着我们可以利用CITRIS的潜在维度在底层数据生成过程中进行干预。为了验证这一点,我们实现了一个函数,该函数能够通过CITRIS学习到的潜在空间对物体的旋转角度进行干预。
# 使用torch.no_grad()上下文管理器来禁用梯度计算
@torch.no_grad()
def encode(imgs):
# 将图像数据从numpy数组转换为torch张量,并取RGB三个通道
imgs = torch.from_numpy(imgs)[..., :3]
# 调整张量的维度顺序,以符合模型的输入要求
imgs = imgs.permute(0, 3, 1, 2)
# 将图像数据归一化到[-1, 1]区间
imgs = imgs.float() / 255.0
imgs = imgs * 2.0 - 1.0
# 使用模型的编码器对图像进行编码
encs = model.autoencoder.encoder(imgs)
return encs
@torch.no_grad()
def rotate_image(img):
# 定义要旋转的角度目标
x_rotation_target = 3
# 对图像进行编码
x_encs = encode(img)
# 通过归一化流传递以解耦潜在空间
input_samples, _ = model.flow(x_encs)
# 获取潜在变量对因果变量的分配
target_assignment = model.prior_t1.get_target_assignment(hard=True)
# 获取映射到x旋转的潜在变量的数量
num_x_rotation_latents = input_samples[:, target_assignment[:, x_rotation_target] == 1].shape[-1]
# 用随机张量替换这些潜在变量
input_samples[:, target_assignment[:, x_rotation_target] == 1] = torch.randn(1, num_x_rotation_latents) * 3
# 从潜在空间的样本中反向流,得到旋转后的潜在表示
input_samples = model.flow.reverse(input_samples)
# 解码并获取新的图像
rotated_image = model.autoencoder.decoder(input_samples)
# 去除旋转图像的批次维度
return rotated_image.squeeze(0)
# 设置绘图参数
fig, axs = plt.subplots(1, 5)
# 从数据集中获取第一张图像
img = causal3d_dataset['images'][0]
# 对图像进行显示和旋转操作的循环
for i in range(5):
if i == 0:
# 显示原始图像
axs[i].imshow(img)
axs[i].set_xlabel('原始图像')
else:
# 显示旋转后的图像
axs[i].imshow(normalize(rotate_image(img[None, :])))
axs[i].set_xlabel(f'随机旋转 {i}')
# 隐藏所有子图的坐标轴
for ax in axs.flat:
ax.set_xticks([])
ax.set_yticks([])
# 调整子图布局并显示
plt.tight_layout()
plt.show()

由于归一化流模型的可逆性,我们确实有能力利用CITRIS的潜在维度对生成数据的因果机制进行干预,以解答“如果…会怎样”的假设性问题。
在特定的场景下,如果我们想要探索改变物体的旋转角度会对生成的图像产生何种影响,我们可以直接对CITRIS的潜在维度进行操作。这让我们能够直观地看到,当茶壶的旋转角度发生变化时,生成的图像会如何随之改变。
3.4.分析潜在空间
为了更深入地了解CITRIS的潜在空间如何响应因果变量值的独立变化,我们设计了一个实验。在这个实验中,我们生成了一个图像序列,通过逐步改变以下几个关键因素来观察图像的变化:首先,我们调整图像中茶壶的位置;接着,我们改变聚光灯的旋转角度;最后,我们改变背景颜色。这一系列的干预操作将帮助我们分析CITRIS的潜在空间是如何捕捉和响应这些因果变量变化的,尽管CITRIS在训练过程中从未直接访问过这些因果变量的真实标签。
# 加载数据滑块数据
data_slider = dict(np.load(os.path.join('CITRIS_DL2', 'data', 'data_slider.npz')))
通过CITRIS-NF的编码器将图像序列传递至归一化流中,我们获取了每个潜在维度的目标值,并将这些值按照它们各自对应的因果变量进行分组。这样,我们可以清晰地识别出哪些潜在维度是专门用于表示特定因果变量的。
@torch.no_grad()
def get_causal_latents(img):
# 对图像进行编码
x_encs = encode(np.expand_dims(img, axis=0))
# 通过归一化流传递以解耦潜在空间
causal_latents, _ = model.flow(x_encs)
# 获取目标分配
target_assignment = torch.argmax(model.prior_t1.get_target_assignment(hard=True), dim=-1)
# 保留将被可视化的因果潜在变量,即位置、聚光灯旋转和背景色调
causal_latents_to_keep = torch.where((target_assignment == 0) |
(target_assignment == 1) |
(target_assignment == 2) |
(target_assignment == 5) |
(target_assignment == 8))
causal_latents = causal_latents.squeeze(0)[causal_latents_to_keep]
target_assignment = target_assignment[causal_latents_to_keep]
# 根据分配对它们进行排序
indices = torch.argsort(target_assignment)
return causal_latents[indices], target_assignment[indices]
接下来,我们使用条形图来直观地展示孤立变化对CITRIS潜在空间的影响。通过滑块,用户可以交互地控制并选择不同的潜在维度进行可视化,从而观察这些维度在不同帧图像中的变化。请注意,为了使用滑块功能,您可能需要在一个支持交互性的环境中(如Colab笔记本)打开相关的笔记本文件。以下是一个简化的GIF动图描述,它展示了通过迭代不同图像时潜在维度的变化。
@widgets.interact(img_id=(0, 29))
def visualize_latents(img_id=0):
img = data_slider['imgs'][img_id]
causal_latents, assignments = get_causal_latents(img)
# 将分配值映射到0、1、2,分别代表物体位置、聚光灯旋转和背景色调
assignments[assignments <= 2] = 0
assignments[assignments == 5] = 1
assignments[assignments == 8] = 2
labels = ['物体位置', '聚光灯旋转', '背景色调']
groups = [labels[i] for i in assignments]
colors = [f'C{assignment}' for assignment in assignments]
fig, axs = plt.subplots(1, 2)
axs[0].imshow(img) # 显示图像
# 绘制条形图,展示潜在维度的变化
axs[1].bar(np.arange(causal_latents.shape[0]), height=causal_latents, color=colors, label=groups)
axs[1].set_ylim(-25, 25) # 设置y轴的范围
# 隐藏所有子图的坐标轴
for ax in axs.flat:
ax.set_xticks([])
ax.set_yticks([])
# 创建图例
handles, labels = plt.gca().get_legend_handles_labels()
by_label = dict(zip(labels, handles))
plt.legend(by_label.values(), by_label.keys(), loc='upper right')
plt.tight_layout() # 调整布局
plt.show() # 显示图像
# 设置滑块的宽度为100%
visualize_latents.widget.children[0].layout.width = '100%'

4. 总结
在本文中,我们深入探讨了CITRIS,这是一种先进的因果表示学习方法,该方法能够从带有干预的图像序列中识别出因果变量。首先,我们阐述了因果表示学习的基本概念,以及这一新兴领域为何令人瞩目。随后,我们描述了我们的目标,即在特定因果环境下识别未知的因果变量,并详细解析了CITRIS是如何工作的。通过实验,我们展示了CITRIS在3D渲染对象场景中能够较为准确地分解因果因素,并演示了如何利用这种因果表示在复杂图像空间中实施干预。展望未来,鉴于因果性在弥补基于统计的机器学习方法中的不足方面具有显著潜力,我们坚信在未来的机器学习发展中,因果性将占据越来越重要的地位。
参考文献
-
I. Schölkopf et al., “Towards Causal Representation Learning,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021.
-
G. Lachapelle et al., “Disentanglement via Mechanism Sparsity Regularization: A New Principle for Nonlinear ICA,” in IEEE Transactions on Neural Networks and Learning Systems, 2021.
-
S. Lippe et al., “iCITRIS: Causal Representation Learning for Instantaneous and Temporal Effects in Interactive Systems,” in IEEE Transactions on Cybernetics, 2022.
-
D. von Kügelgen et al., “Self-Supervised Learning with Data Augmentations Provably Isolates Content from Style,” in IEEE Transactions on Image Processing, 2022.
-
J. Brehmer et al., “Weakly Supervised Causal Representation Learning,” in IEEE Transactions on Machine Learning and Cybernetics, 2022.