组合总和
- 39. 组合总和
- 题目描述
- 初始思路
- 后续分析
- 40. 组合总和 II
- 题目描述
- 思路(参考代码随想录)
39. 组合总和
题目🔗
题目描述
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
初始思路
好久没有做回溯的题了,首先画图分析一下:
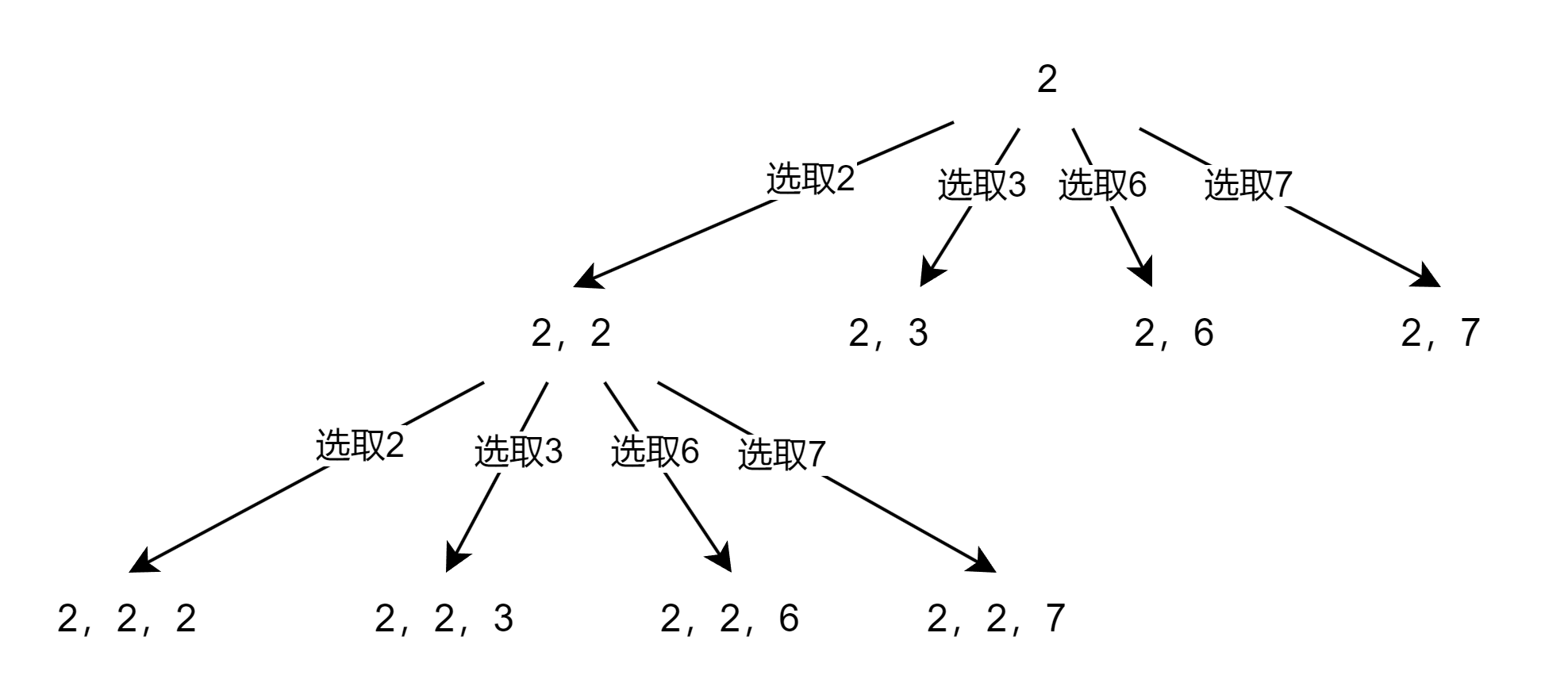
因为这题可以重复选取,那么我们每次选取都是在一个相同的集合中(例如candidates={2, 3, 6, 7})。所以除了第一次选择的元素之外,我们之后所做的操作都是相同的,那么就可以定义一个cur_idx来表示我们首次选择的元素的index,用一个一维数组vec来记录当前路径,当vec中的和等于target时,就把这条路径放入最终结果集result中。于是我开始写的代码就是这样的:
class Solution {
public:
void backtracking(int cur_idx, int target, vector<int>& candidates, vector<int>& vec, vector<vector<int>>& results){
// 终止条件
if(accumulate(vec.begin(), vec.end(), 0)==target){
if(find(results.begin(), results.end(), vec)==results.end()) results.push_back(vec);
return;
}
for(int i = 0; i < candidates.size(); i++){
if(accumulate(vec.begin(), vec.end(), 0)+candidates[i]<=target)
vec.push_back(candidates[i]);
backtracking(i+1, target, candidates, vec, results);
vec.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<int> vec;
vector<vector<int>> results;
backtracking(0, target, candidates, vec, results);
return results;
}
};
但是不出意料的没通过。。
后续分析
还是认真地走一下三部曲吧QAQ
- 递归函数参数
和我上面分析的一样:
vector<int>& vec;
vector<vector<int>>& results;
void backtracking(int cur_idx, int sum, int target, vector<int>& candidates);
把vec和results放在类成员变量中,就不用写在函数入口。sum是当前路径统计的和。
- 递归终止条件
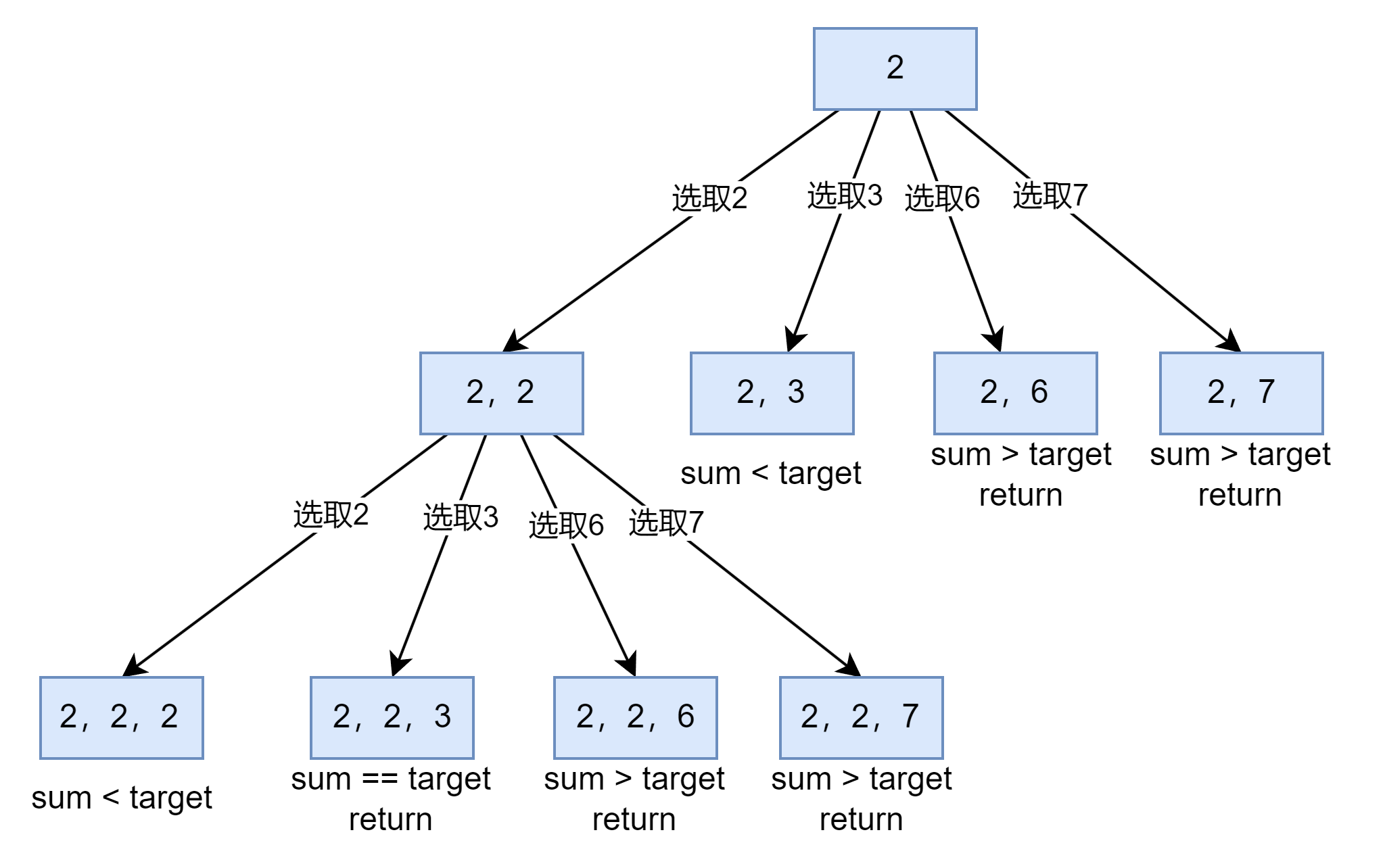
从上图来看,当前路径vec的总和sum大于等于target时,就要返回,并且当sum==target时,我们就要收集结果。
if(sum > target) return;
if(sum == target) {
result.push_back(vec);
return;
}
啊,可以看出我刚开始忽略了sum>target的情况。
- 单层搜索逻辑
这层的重点在于重复选取的实现,先看代码:
for (int i = cur_idx; i < candidates.size(); i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i); // 关键点:不用i+1了,表示可以重复读取当前的数
sum -= candidates[i]; // 回溯
path.pop_back(); // 回溯
}

整体的逻辑就是我上面这张图这样(第二行的{2, 3} sum=5后面应该还有哈,但是我懒得画了)。
所以整体代码是:
class Solution {
public:
vector<int> vec;
vector<vector<int>> results;
void backtracking(int cur_idx, int sum, int target, vector<int>& candidates){
// 终止条件
if(sum == target){
results.push_back(vec);
return;
}
if(sum > target) return;
// 单层逻辑
for(int i = cur_idx; i < candidates.size(); i++){
vec.push_back(candidates[i]);
sum += candidates[i];
backtracking(i, sum, target, candidates);
sum -= candidates[i];
vec.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vec.clear();
results.clear();
backtracking(0, 0, target, candidates);
return results;
}
};
40. 组合总和 II
题目🔗
题目描述
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
思路(参考代码随想录)
这题的难点在于集合中有重复元素,但是结果中不能包含重复的组合。
这里我们要明白重复有两种情况:树枝重复和树层重复。
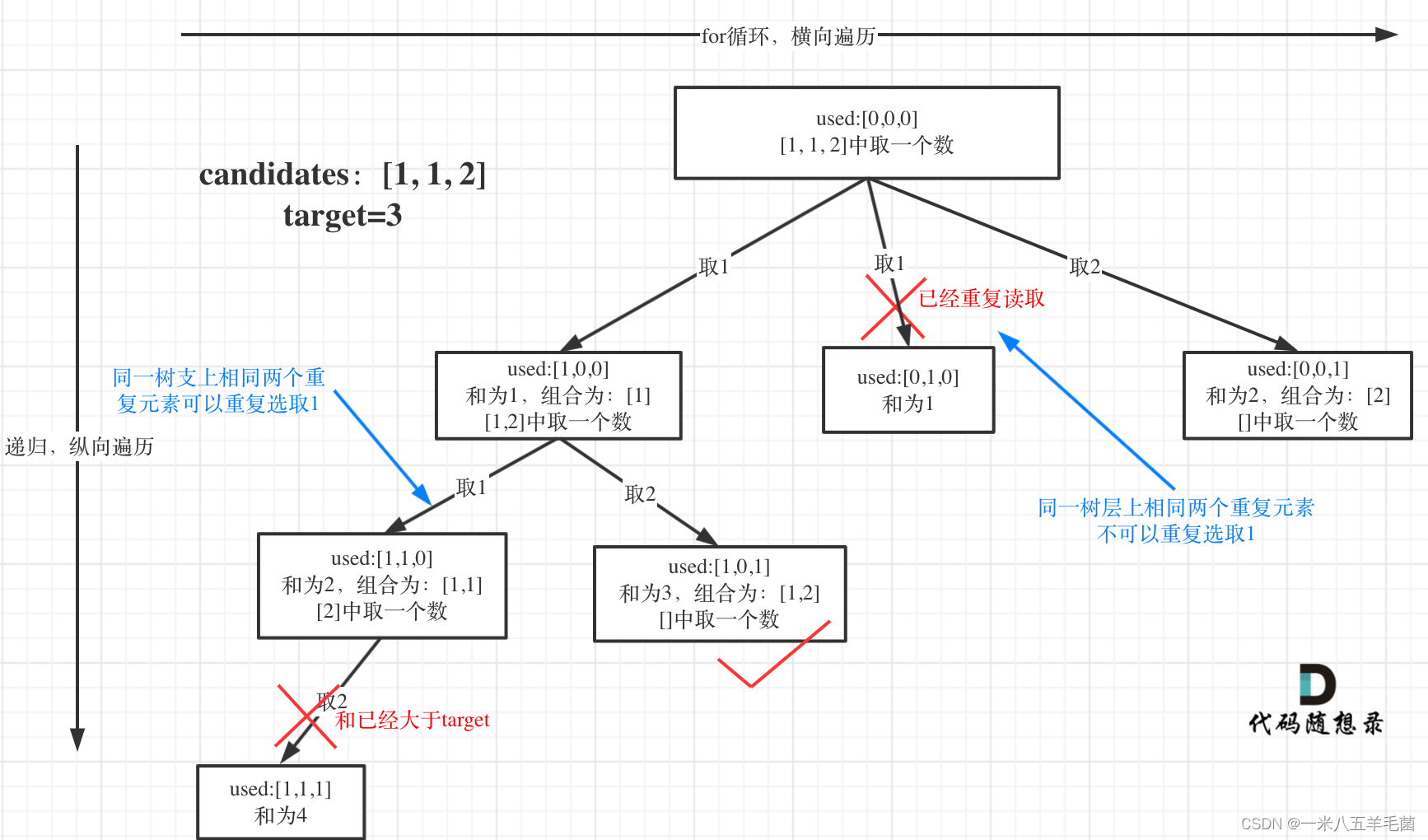
借用卡哥的图来说明一下。树枝重复是左边的情况,树层重复是中间的情况。而这题不能出现的是树层重复。这里我们用一个used数组来表示每一个数是否被使用。
从上面这个图可以看出,当我们在树的第二层(集合已经被排序过了,相同元素挨在一起),当我们取第二个1的时候,也就是candicates[1],而前面的candidates[0]也是1,说明已经重复读取了,所以我们判断在同一树层是否重复读取的逻辑是i > 0 && candidates[i] == candidates[i-1] && used[i-1] == 0。
整体代码如下:
class Solution {
public:
vector<int> path;
vector<vector<int>> results;
void backtracking(int index, int target, vector<int>& candidates, int sum, vector<int>& used) {
if(sum == target) {
results.push_back(path);
return;
}
if(sum > target) {
return;
}
for(int i = index; i < candidates.size(); i++) {
if(i > 0 && candidates[i] == candidates[i-1] && used[i-1] == 0)
continue;
sum += candidates[i];
path.push_back(candidates[i]);
used[i] = 1;
backtracking(i+1, target, candidates, sum, used);
sum -= candidates[i];
path.pop_back();
used[i] = 0;
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<int> used(candidates.size(), 0);
sort(candidates.begin(), candidates.end());
path.clear();
results.clear();
int sum = 0;
backtracking(0, target, candidates, sum, used);
return results;
}
};