\qquad 想要完全理解二维树状数组,要先完全理解一维树状数组。这里给大家推荐一个视频:五分钟丝滑动画讲解 | 树状数组。建议大家先看一遍视频再来看下面的讲解。
\qquad 在一维树状数组中, t r e [ i ] tre[i] tre[i] 可以理解为以 i i i 为结尾的长度为 l o w b i t ( i ) lowbit(i) lowbit(i) 的数之和。
\qquad 列如: l o w b i t ( 12 ) = 4 lowbit(12)=4 lowbit(12)=4 所以 t r e [ 12 ] tre[12] tre[12] 表示以 12 12 12 结尾的长度为 4 4 4 的数的和,即下图中标红的地方。
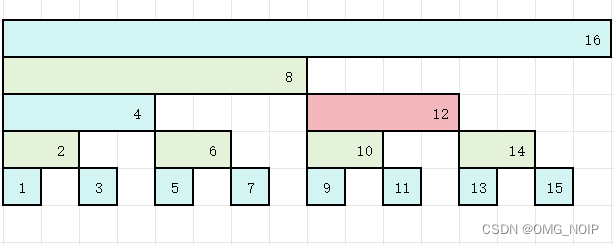
\qquad 那么我们可以尝试用 t r e [ i ] [ j ] tre[i][j] tre[i][j] 表示右下角在第 i i i 行,第 j j j 列,宽为 l o w b i t ( j ) lowbit(j) lowbit(j),高为 l o w b i t ( i ) lowbit(i) lowbit(i) 的矩阵。
\qquad 例如: l o w b i t ( 10 ) = 2 lowbit(10)=2 lowbit(10)=2 所以 t r e [ 10 ] [ 12 ] tre[10][12] tre[10][12] 表示右下角在第 10 10 10 行,第 12 12 12 列,宽为 4 4 4,高为 2 2 2 的矩阵,即下图中标红的地方。
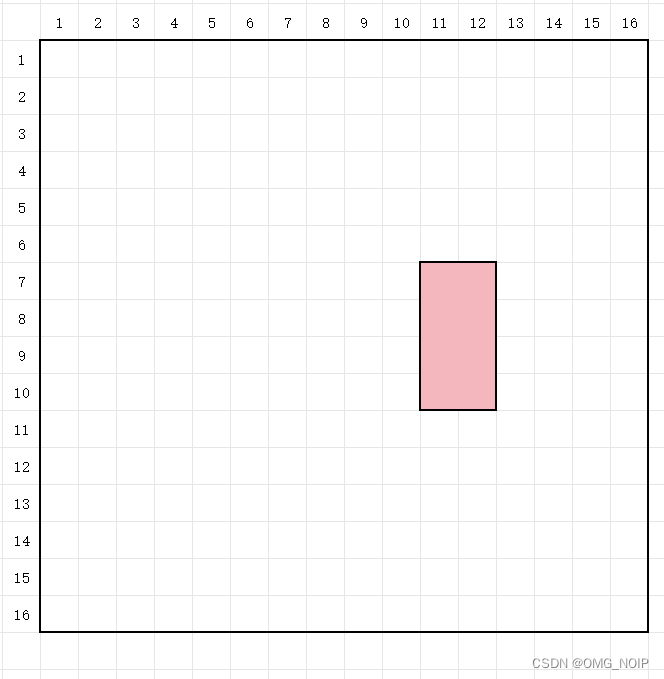
\qquad 在一维树状数组中, 12 12 12 的前缀和为 t r e [ 8 ] + t r e [ 12 ] tre[8]+tre[12] tre[8]+tre[12],即下图中标红的两个地方。
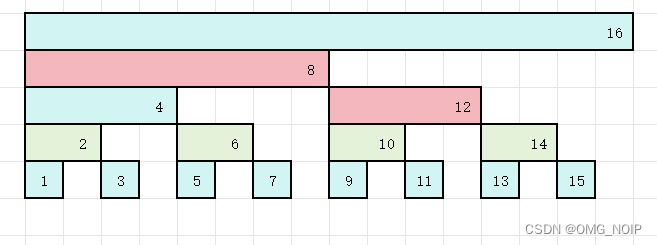
\qquad 而 13 13 13 得前缀和为 t r e [ 8 ] + t r e [ 12 ] + t r e [ 13 ] tre[8]+tre[12]+tre[13] tre[8]+tre[12]+tre[13],即下图中标紫的三个地方。
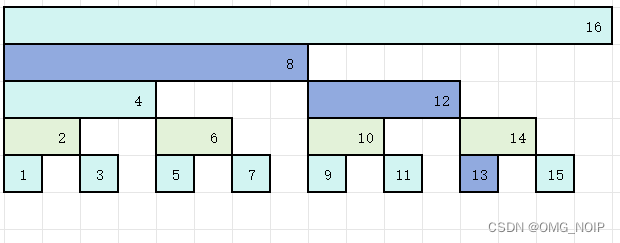
\qquad 我们把它们对应到二维矩阵中:
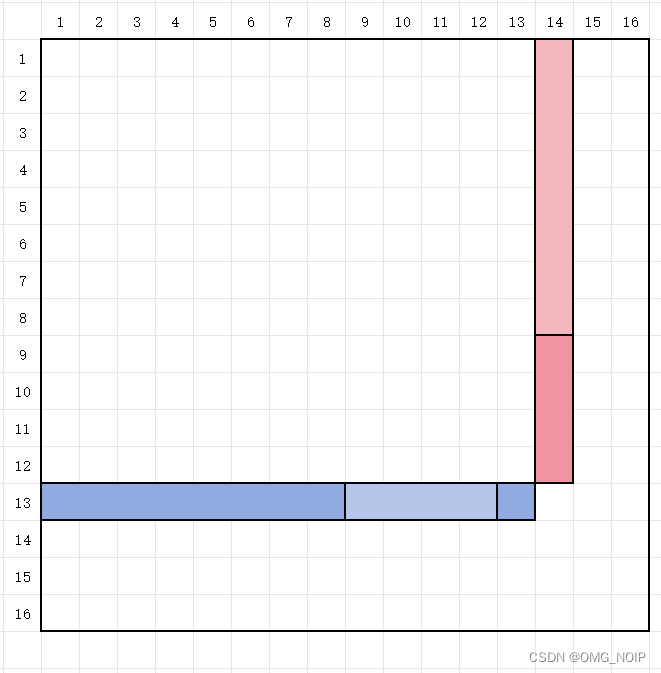
所以要求右下角在第 12 12 12 行,第 13 13 13 列的矩阵前缀和,就需要将下图标绿的矩阵求和。
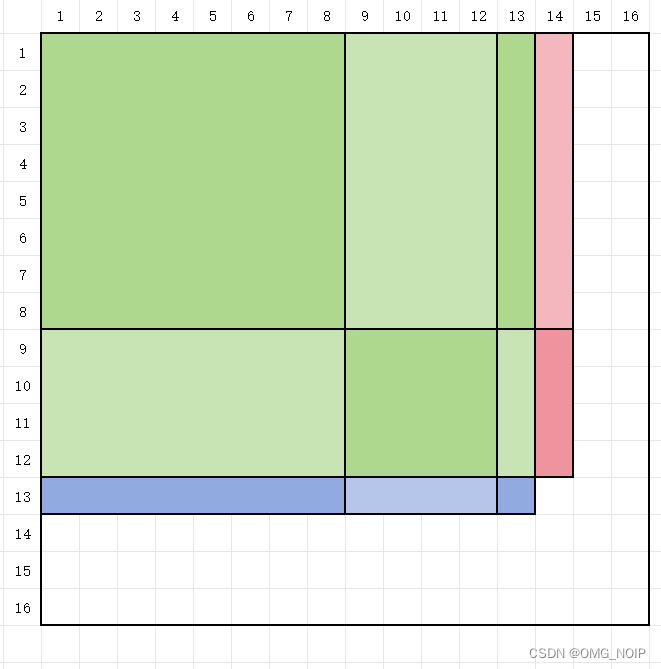
\qquad
那么在代码中,我们就只需要写两层循环,一层遍历行的的
l
o
w
b
i
t
lowbit
lowbit,一层遍历列的的
l
o
w
b
i
t
lowbit
lowbit,将所有遍历到的矩阵求和。
// 查询左上角在 第一行第一列,右下角在第 H 行第 L 列的矩阵之和
inline ll query(ll H,ll L){
ll res=0;
// 遍历行的 lowbit
for(ll i=H;i>=1;i-=lowbit(i)){
// 遍历列的 lowbit
for(ll j=L;j>=1;j-=lowbit(j)) {
res+=tre[i][j];
}
}
return res;
}
\qquad 好,那么你已经学会了二维树状数组的区间查询,接下来我们看单点修改。
\qquad 不想画图了,原理和上面的差不多,直接上代码。
// 将第 H 行,第 L 列的数加上 k
inline modify(ll H,ll L,ll k){
// 遍历行的 lowbit
for(ll i=H;i<=n;i+=lowbit(i)){
// 遍历列的 lowbit
for(ll j=L;j<=m;j+=lowbit(j)){
tre[i][j]+=k;
}
}
}
\qquad 最后上一个完整代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll tre[105][105],n,m;
inline ll lowbit(ll k){return k&(-k);}
// 将第 H 行,第 L 列的数加上 k
inline modify(ll H,ll L,ll k){
// 遍历行的 lowbit
for(ll i=H;i<=n;i+=lowbit(i)){
// 遍历列的 lowbit
for(ll j=L;j<=m;j+=lowbit(j)){
tre[i][j]+=k;
}
}
}
// 查询左上角在 第一行第一列,右下角在第 H 行第 L 列的矩阵之和
inline ll query(ll H,ll L){
ll res=0;
// 遍历行的 lowbit
for(ll i=H;i>=1;i-=lowbit(i)){
// 遍历列的 lowbit
for(ll j=L;j>=1;j-=lowbit(j)) {
res+=tre[i][j];
}
}
return res;
}
signed main(){
ios::sync_with_stdio(false);
cin>>n>>m;
while(1){
ll op,H,L,k;
cin>>op>>H>>L;
if(op==1){
cin>>k;
modify(H,L,k);
}
else cout<<query(H,L)<<endl;
}
return 0;
}
有不懂的私信我,我都会尽量回的。ok,讲完了。